
Vibration fingerprints

Figure 1: Not every object sounds good when you bang it.
Many things make a noise when you hit them, but not many are commonly used to play music — why is that? To answer this question we start with an important result from vibration theory about any object which is set into vibration by plucking or tapping and then left alone for the sound to ring on and gradually die away. The sound always consists simply of a mixture of decaying sine waves, each corresponding to a particular resonance or vibration mode of the structure. To give a "vibration fingerprint" of the sound we need to know three things about each of these sine waves: the frequency, the amplitude and the decay rate or damping. Frequency corresponds approximately to the musical attribute pitch, amplitude to loudness, and the decay rate determines whether the sound goes ping (slow decay) or thud (fast decay).
Listen to the example below to hear the effect of changing decay rate, keeping everything else the same. The three sounds go from metallic to wooden: variation in damping is the main thing that makes different materials sound distinctive.
| The effect of changing decay rates |
For any particular object the frequencies and decay rates are fixed and characteristic of that object, but the amplitudes can be varied by the performer depending on how and where it is tapped or plucked. (This description does not apply to things like a bowed violin string, whose vibration is sustained by the bow feeding in energy. Such vibrating systems are more complicated, and will be ignored entirely in this article: see Why is the violin so hard to play? for some of the story of how a bowed violin string behaves.)
We look first at a vibrating object which everyone agrees you can use to play music: a stretched string, as on a guitar or piano. When you pluck or strike a stretched string, you always hear a sound with a definite musical pitch. The pitch can be changed by varying the length, tension or weight of the string, all familiar to musicians. What is special about the string, compared to the sound of banging a saucepan or a table? The simplest mathematical description of the vibration of a stretched string reveals a pattern in the set of resonance frequencies. Once the lowest (or \emph{fundamental}) frequency has been fixed by choosing the weight, tension and length of the string, then all the other frequencies are whole-number multiples: if the first is $f$ , then the second is $2f$ , the third $3f$ and the $nth$ is $nf$ . The frequencies are called the \emph{natural frequencies} or \emph{overtones}, and this simple numerical pattern relating them is called a \emph{harmonic series}: so a stretched string has natural frequencies which are harmonic.
Each natural frequency is associated with a particular pattern of vibration, called a mode shape. The first few mode shapes of a vibrating string are shown here:
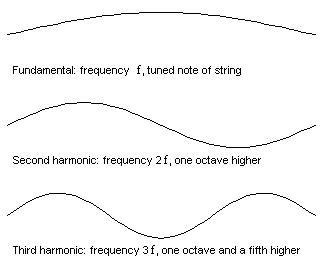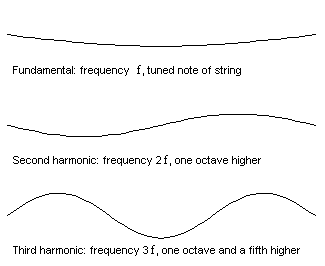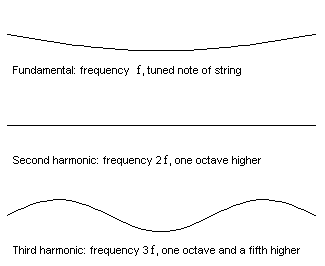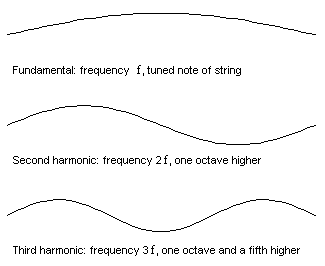
Figure 2: The first few vibration modes of a vibrating string.
Harmonics and non-harmonics
The harmonic pattern of natural frequencies is the key property: it is an empirical fact about the way our ears and brains function that we recognise sounds in which the component sine waves are harmonically related as being special, and we describe that by saying that they have a definite musical pitch. Most vibrating objects have natural frequencies which are not harmonically related, and so do not produce definite pitch. The art and science of making a tuned percussion instrument is all about manipulating the natural frequencies, or at least a few of them, into harmonic relations. This has been achieved in many different and ingenious ways, and we will look at some examples in this article.
But before that we should listen to some sounds to see if the claim about harmonic natural frequencies is really true. From a given vibration fingerprint, a recipe of frequencies, amplitudes and decay rates, it takes only a very simple computer program to create the sound: this process is called additive synthesis and is the basis of one kind of electronic musical instrument. We can also use a computer for the reverse process: to record a sound, then analyse it into its component decaying sine waves to find out which frequencies are present and how they relate to each other. (You can find out more about this in our interviews with an audio software engineer and a computer music researcher.)
Here are some sounds, all synthesised from sine waves. A simple scale passage has been created. For each note the different sound samples all have the same fundamental frequency and the same pattern of amplitudes varying with frequency. The pattern of higher overtones is different in each sound sample. (For the full details of all the synthesised sounds see here.) The first sound A should resemble a guitar string: it has exactly harmonic overtones, and it is the reference standard for comparing with the others. Now listen to the two pairs B/C and D/E, and for each pair consider whether one sounds more "musical" than the other. You can recognise the scale passage in all four sound samples, but if you were buying an instrument in order to play music you would probably choose C rather than B, and E rather than D.
| Sound A |
Sound B |
| Sound C |
|
| Sound D |
Sound E |
Bars and xylophones
The patterns of natural frequencies explain this preference. The sounds B and C relate to vibrating bars: B has frequencies characteristic of a uniform bar, a case which can be analysed mathematically, while C uses the frequency pattern determined by analysis of the sound of a carefully adjusted xylophone bar. Relative to the fundamental frequency the two sets of frequencies are [1, 2.76, 5.40, 8.93, 13.34, 18.64, 24.82] for B and [1, 3.96, 10.67, 19.17, 27.02] for C. The shapes of the vibration modes are rather similar in both cases: here are plots of the first few modes for the textbook case of the uniform bar:
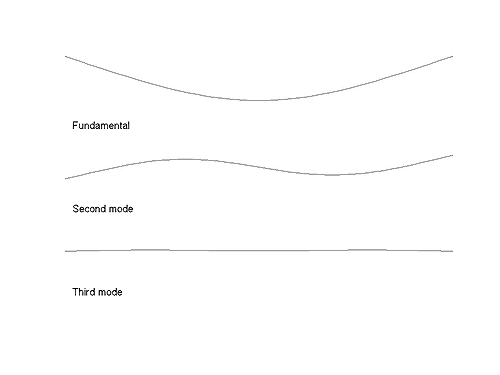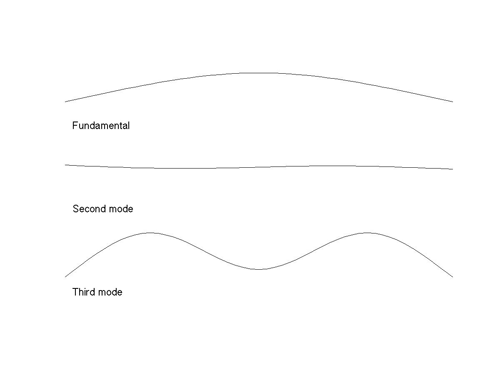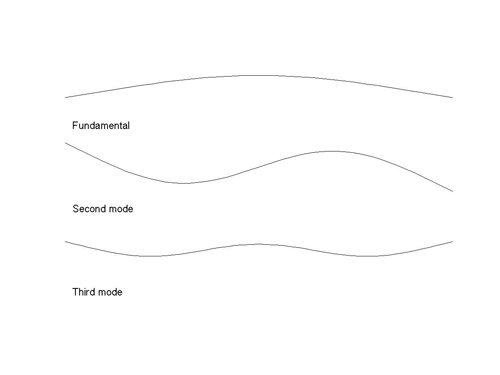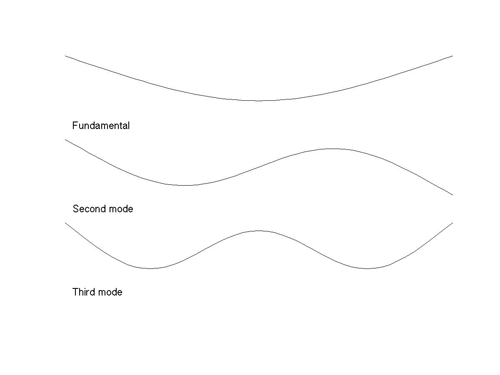
Figure 3: The first few modes for the uniform bar.
To explore bar modes in more detail, look at the falstad website and choose the Bar waves applet.
So what has been done to the xylophone bar to make the frequencies so different? The answer is that the instrument maker has carved wood away from the underside of the bar, as shown here:

Figure 4: A xylophone. Some wood on the underside of the bar has been carved away.
This thinning of the centre of the bar makes the lowest frequency move down, and allows the tuner to achieve approximately a 4:1 ratio between the first two frequencies. The textbook bar, by contrast, does not have a frequency ratio close to a whole number. This rather small move in the direction of harmonic overtones is enough to make the sound difference you have heard, and to make the bar significantly more musical, even though the 4:1 ratio is not exact.
The Caribbean steel pan
 Figure 5: A Caribbean steel drum.
Figure 5: A Caribbean steel drum.
The sounds D and E relate to a very different tuned percussion instrument. Sound D is based on another simple system which can be mathematically analysed: a thin rectangular plate which is fixed around its edges. Sound E uses frequency ratios measured from one note of a Caribbean steel pan. The notes of the steel pan are all made from a thin metal plate, but the details have been carefully adjusted by the maker to give some harmonic relations between the first few natural frequencies. The frequency ratios for these examples are: for sound D, [1, 1.88, 3.12, 3.35, 4.00, 5.41, 5.47, 6.65] and for sound E, [1, 2.00, 2.48, 4.01, 4.13, 4.98, 5.50, 7.58]. Notice that sound E has ratios close to 2, 2.5, 4 and 5.
The steel pan has an interesting history, and is one of the most recent inventions among the tuned percussion family. Slaves on the plantations in the Caribbean islands were forbidden from using their traditional musical instruments because these were a focus for political protest. They learned to make musical instruments using other discarded objects such as bamboo sticks, empty bottles and biscuit tins, and a tradition of carnival bands grew up around these instruments. Around the end of the second world war American military bases in the islands were abandoned, and large numbers of discarded empty oil drums were left behind. The modern steel pan was developed by experimenting with ways to use this resource using the tricks developed earlier with biscuit tins and paint cans.
The top of an oil drum is first hammered into a bowl shape, then the areas which are to form the individual notes are hammered back from the underside of the bowl so that they form relatively flat patches, surrounded by the curved bowl. A pan maker can be seen at work in this picture.

Figure 6: A steel drum maker in action. You can see the flattened areas corresponding to different notes.
This arrangement of a flattish patch of metal in a bowl is what allows several different notes to be made out of the same oil drum head. Vibration modes are possible in which the metal within the flat patch vibrates, without the vibration spreading into the bowl. The essential reason is similar to the principle of corrugated iron roofing sheets: if a thin metal sheet is curved, and you then try to bend the sheet in the perpendicular direction to the curvature, it is much stiffer than the flat sheet would have been. This stiffening leads to an effect of total internal reflection of the vibration at the edges of the flat patch. Several of these confined vibration modes can occur in each note area, and by adjusting the size, shape and thickness distribution of the note, the maker can achieve the desired harmonic relations which lead to a pleasing musical sound.
Tuned drums
The steel pan is sometimes called the steel drum, but we now turn to true drums, which use a stretched membrane of some kind as the vibrating element. As with the earlier examples of the bar and the plate, an ideal circular membrane is a problem which can be analysed mathematically, leading to a set of mode shapes which are illustrated below. These are associated with natural frequencies which are not harmonically related, as indicated in the figure. The result is that a simple drum (like the bass drum of a rock band) does not have a clear musical pitch. As with the bar modes, you can explore membrane vibration in more detail at falstad by choosing the Circular membrane applet.
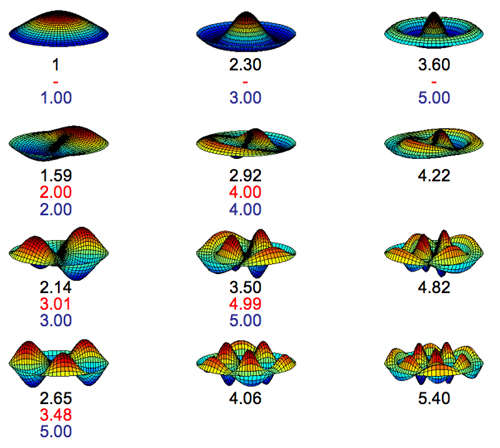
Figure 7: A set of mode shapes for the drum. The numbers give the frequency ratios (where available) for the ideal membrane (in black), the kettle drum (in red) and the tabla (in blue).
Two different tricks have been used by different cultures to manipulate a few of these natural frequencies to produce harmonic relations. In the western musical tradition we are most familiar with the kettledrum. This has a specially-shaped metal bowl under the drum membrane, and effects associated with air movement in this bowl shift the natural frequencies a little to allow some harmonic relations to be achieved. The frequency relations between these tuned modes are indicated in the figure. Notice that not all the low modes are tuned. The audible effect of the unwanted modes in the top row of the plot is reduced by two methods. First, a kettledrum player does not hit in the centre of the drum, but towards the edge. This emphasises the excitation of the tuned modes relative to the untuned ones. Second, notice that the modes in the top row are the only ones for which the vibration produces a net change of volume of the air inside the "kettle" under the membrane. By putting a small hole in the bottom of the bowl, energy associated with these modes is dissipated by air friction as the changing volume causes air to blow in and out of the hole.
 Figure 8: A tabla. Photo: Lestat.
Figure 8: A tabla. Photo: Lestat.
A more impressive type of tuned drum was developed in India, known as the tabla. (Strictly, the tabla is a pair of drums played together, but for the purposes of this discussion we will use the name for one tuned drum.) A tabla has a dark circle on the middle of the stretched membrane. This is a painstakingly-applied patch of clay material, which gives a distribution of added mass. The vibration modes are modified, and a skilled drum tuner can achieve a remarkable number of harmonic relations between the low modes, as shown in the final set of frequency ratios in the figure. To achieve this effect, over 100 separate thin layers of clay were needed.
| Sound F |
| Sound G |
| Sound H |
Sounds F, G and H let you compare the effect of these untuned and tuned drums. The scale passage is a little unnatural for these instruments, but the effect of the tuning is conveyed clearly enough. The tabla has so many tuned modes that the sound resembles the string of sound A: it doesn’t really sound like a drum at all!
About the author
After a first degree in mathematics at Cambridge, Jim Woodhouse did a PhD on the acoustics of the violin, in the Department of Applied Mathematics and Theoretical Physics at Cambridge (this work being inspired by a hobby interest in building instruments). He then worked for an engineering consultancy firm for a few years, on a variety of problems in structural vibration, before joining the Engineering Department of the University (in 1985) as Lecturer, then later Reader and Professor. His research interests all involve vibration, and musical instruments have continued to form a major part.