How many melodies are there?
The equivalent of a writer staring at a blank page, wondering how to fill it, is a composer staring at the 88 black and white notes on a piano wondering how to compose a melody that's never been heard before. How can one possibly take the eight notes of a standard scale and write a brand new melody when so many great melodies have already been written? Perhaps they've all been taken!
How many combinations are there?
So, to counter the fear of there being no new melodies, I thought it would be interesting to examine the number of melodies available to a composer looking at his blank stave to see how many there potentially are.
The first thing to do is to lay down some ground rules. These are:
- The melodies will be a single stream of notes — no chords, counter-melodies or basslines — just a single line of music. Remember the "old grey whistle test"? If it can be played on a tin whistle — it's a melody.
- For the first section I've discounted rhythm so as to focus only on the permutations of notes.
- All melodies should be contained within an octave — C to C' inclusive.
- Any of the 13 chromatic notes of the octave can be used. I've not restricted this to just a major or minor scale as many great melodies use accidentals (the black notes in a C major scale). So we can include all of the notes within the octave, including the octave jump (from C to C') as otherwise Over the Rainbow would not count as a melody! The notes are: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C'.
We will tackle this problem by starting with the simplest possible melody — one consisting of two notes — and then building up the melody length one note at a time until we see a pattern that can be turned into a formula.
Two note melodies
How many two note melodies can be written within an octave? This one is easy and all combinations can be written out:
| First note | Second note | Pitch difference (semitones) |
| C | C | 0 |
| C | C# | 1 |
| C | D | 2 |
| C | D# | 3 |
| C | E | 4 |
| C | F | 5 |
| C | F# | 6 |
| C | G | 7 |
| C | G# | 8 |
| C | A | 9 |
| C | A# | 10 |
| C | B | 11 |
| C | C' | 12 |
| First note | Second note | Pitch difference (semitones) |
| C' | C' | 0 |
| C' | B | -1 |
| C' | A# | -2 |
| C' | A | -3 |
| C' | G# | -4 |
| C' | G | -5 |
| C' | F# | -6 |
| C' | F | -7 |
| C' | E | -8 |
| C' | D# | -9 |
| C' | D | -10 |
| C' | C# | -11 |
| C' | C | -12 |
Now, you might be wondering why combinations like G# - F and E – A are not included. This is because we are only interested in relative pitch, not absolute notes. For the purposes of this exercise the melody C – C is identical to D – D or G – G as they are all unison melodies (i.e., they have 0 as their pitch difference). That's why we won't count the unison melody C' – C' — unison was already covered in the first table by C – C.
Having excluded C' - C' we have a total of 25 exciting two-note melodies!
Three note melodies
The number of three note melodies rises quite sharply, but not so much that they can't also be written out.
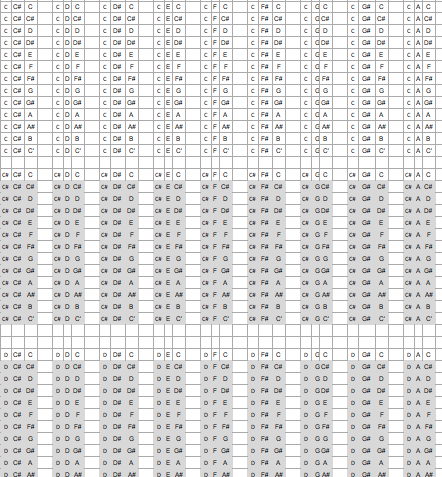
A small extract of the spreadsheet that lists all 2197 three-note combinations with duplicates in grey. You can see the whole spreadsheet here.
We can start by listing all possible combinations of three notes and then crossing out those that are duplicates. It turns out that it's easy to find duplicates: they are exactly those sequences of notes that don't have any C in them. Any melody without a C can always be moved down the scale until its lowest note becomes a C. Therefore, any melody without a C is a duplicate of a melody that does contain a C. To count all melodies, all we have to do is to count all sequences of notes than contain a C.
There are exactly 2,197 three-note combinations, out of which 1,728 don't contain a C. So there is a total of 2,197 – 1,728 = 469 three note melodies.
Not bad!
Four to infinity
Now, writing down all possible combinations of notes and picking out the ones with a C is not a very efficient way of exploring further, so we need an equation that will describe the increase in melodies. Suppose we are counting melodies made out of 
notes (so we’ve already covered 
and 
). There are 13 choices for what the first note could be (one of C through to C’), 13 choices for the second note, and so on. This means that the number of all sequences of notes is
![\[ \underbrace{13 \times 13 \times ... \times 13}_{n} = 13^ n. \]](/MI/acfe84d0716048a81bf4bd49245092cf/images/img-0004.png) |
From this we need to subtract the sequences that don’t have a C in them. For such a sequence there are 12 choices for the first note, 12 choices for the second note, and so on. So the number of all sequences of notes that don’t contain a C is
![\[ \underbrace{12 \times 12 \times ... \times 12}_ n = 12^ n. \]](/MI/acfe84d0716048a81bf4bd49245092cf/images/img-0005.png) |
Which tells us that the number of sequences of notes that do contain a C (the number of melodies) is
![\[ 13^ n - 12^ n. \]](/MI/acfe84d0716048a81bf4bd49245092cf/images/img-0006.png) |
We can even be more general and find the number of melodies for any scale. If the number of notes in the scale is 
(so in our case 
) then the number of melodies that contain notes is
![\[ s^ n - (s-1)^ n. \]](/MI/acfe84d0716048a81bf4bd49245092cf/images/img-0009.png) |
But let’s return to our example with 
Substituting ever larger numbers for 
— the length of the melody — gives us the following answer to our original question, the number of potential melodies within an octave:
| Length of melody | No of possible melodies |
| 2 | 25 |
| 3 | 469 |
| 4 | 7,825 |
| 5 | 122,461 |
| 6 | ca. 1.84 million |
| 7 | ca. 26.9 million |
| 8 | ca. 385 million |
| 9 | ca. 5.4 billion |
| 10 | ca. 75 billion |
So, a mere ten note melody will produce over 75 billion potential melodies of 13 notes within the octave! It's going to take our composer a while to work his way through those. A computer would find it easier — if anyone out there produces a program that cycles through all of them, then please let us know!
Bring on the rhythm
It would be nice to factor in rhythm as well, just to be completist, as very few melodies are sequences of exactly the same length of notes.
Luckily this is much easier to compute. Potentially note lengths can be anything between a semiquaver (a sixteenth note) and a semibreve (a whole note). (I'm discounting hemi-demi-semiquavers!) Rather than include every single variation I think these would be a sensible selection of notes that would be available to use:
This means there are 8 different possible lengths of a note, and each new note added to the sequence multiples the number of combinations by 8. for a sequence of 
notes the formula that counts the different rhythm variations is simply 
which gives us the final calculation as below:
| Length of melody | No of possible note combinations | Rhythm variations (ignoring melodies) = 8n | Number of melodies (note combinations multiplied by rhythm variations |
| 2 | 25 | 64 | 1600 |
| 3 | 469 | 512 | 240,128 |
| 4 | 7,825 | 4,096 | 32 million |
| 5 | 122,461 | 32,768 | 4 billion |
| 6 | ca. 1.84 million | 262,144 | 4.8 x 1011 |
| 7 | ca. 26.9 million | ca. 2.1 million | ca. 5.6 x 1013 |
| 8 | ca. 385 million | ca. 16.8 million | ca. 6.4 x 1015 |
| 9 | ca. 5.4 billion | ca 1.3 x 108 | ca. 7.02 x 1017 |
| 10 | ca. 75 billion | ca. 1.1 x 109 | ca. 8.25 x 1019 |
Or, for that final number:
There are around 82,500,000,000,000,000,000 melodies that are 10 notes long.
That's a fair few to work through! A very rough approximation shows it's over 2.6 trillion years worth of material. And as mentioned at the start, this doesn't even begin to take into account the variations provided for by harmonisation, orchestration, tempo, or heavens above — bringing in a new counter melody!
So I think the message is: there is no excuse for writers' block.
About the author
Oli Freke is a London based musician and composer who's variously supported the Human League with electro band Cassette Electrik, written for TV and recently had club chart success with track Line-1. He is currently looking forward to working through all 8.25 x 1019 melodies in due course.