
Euclid of Alexandria
Euclid of Alexandria was a Greek mathematician who lived over 2000 years ago, and is often called the father of geometry. Euclid's book The Elements is one of the most successful books ever — some say that only the bible went through more editions. It was also the earliest known systematic discussion of geometry. In it Euclid laid down the rules of geometry.
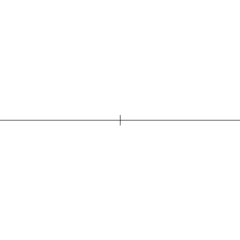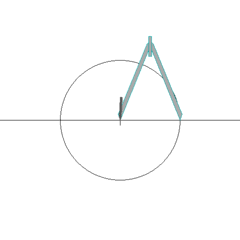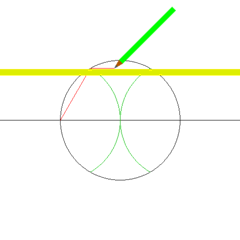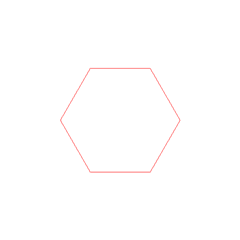
Euclid was interested in all the things you could do with a straight edge (a ruler with no marks) and a compass. He came up with his own set of five rules that described some basic things you could do with these tools, as well as some facts about angles and lines he thought were obviously true and didn't need to be explained.
- Given any two points, you can draw a straight line between them (making what's called a line segment).
- Any line segment can be made as long as you like (that is, extended indefinitely).
- Given a point and a line segment starting at the point, you can draw a circle centred on the given point with the given line segment as its radius.
- All right angles are equal to each other. (This may sound a bit strange, but you can find out more here.)
- If you draw a line segment across two straight lines and it creates two angles on the same side which add to less than two right angles, then those two straight lines intersect. (This axiom is equivalent to saying that the angles in a triangle add up to 180 degrees.)
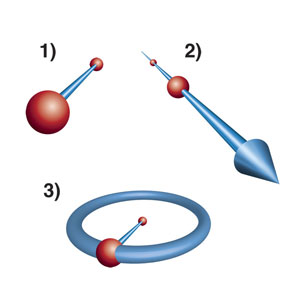
The first three axioms.
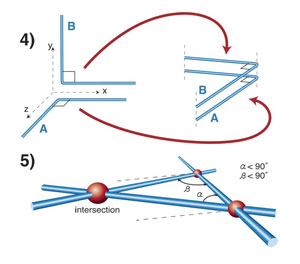
Axioms 4 and 5.
There are lots of nice things you can do with Euclid's axioms. For example, you can draw a regular hexagon:
Animation by Aldoaldoz.
Or you can bisect an angle, that is, you can divide it into two equal angles:
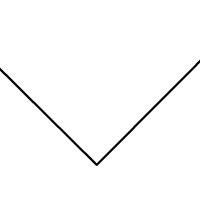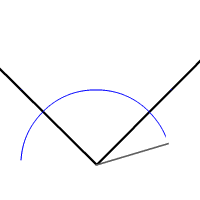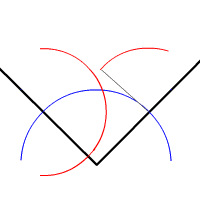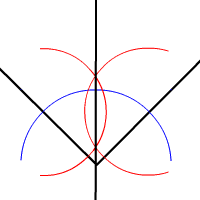
Indeed, these are the tools and methods that stone masons used to create their beautiful decorations and windows in churches and cathedrals. (You can read more here.)
The fifth axiom, however, caused mathematicians some problems: they though that it should actually be a consequence of the first four facts. Their attempt to prove it eventually guided them into the weird and wonderful world of non-Euclidean geometry. Find out more here.