
If you like a drink, then a Klein bottle is not a recommended receptacle. It may look vaguely like a bottle, but it doesn't enclose any volume, which means that it can't actually hold any liquid. Whatever you pour "in" will just come back out again.
How do you construct such a strange thing and why would you want to construct it? The mathematician Felix Klein, who discovered the bottle in 1882, described it as a surface that "can be visualised by inverting a piece of a rubber tube and letting it pass through itself so that outside and inside meet".
It's obvious that the Klein bottle, just like the more familiar sphere, is a closed surface: it's finite in the sense that you can fit it into a finite region of space, but an ant could walk around on it forever without ever encountering a boundary or falling over an edge. Unlike the sphere, which has an inside and an outside, the Klein bottle is one-sided: walking around, our ant could reach both sides of each point of the surface. This is why the bottle encloses no volume, and it also answers the "why" question: the Klein bottle is interesting because we don't encounter many one-sided shapes in nature. (See here for another very pretty picture of a Klein bottle.)

The Möbius strip is one-sided - view the animated version. (Image and animation by Konrad Polthier.)
If this is a bit confusing, think of a simpler example of a one-sided surface: the famous Möbius strip. You can make one by taking two ends of a strip of paper, giving the strip a twist, and then gluing the ends together. By using a strip of paper whose two sides have different colours, say green and orange, it's easy to convince yourself that the resulting Möbius strip is one-sided. Once you have twisted and glued, you'll find that you can reach every orange point from every green point without having to pierce through the paper or climbing over its edge.
Unlike the Klein bottle, the Möbius strip does have a boundary — it is made up of the two non-glued edges of the original strip. But there is a link between the two. If you take two Möbius strips and create a closed shape by joining their boundaries using an ordinary two-sided strip, as shown below, what you get is exactly the Klein bottle.
band whose back and front sides are colored white and blue respectively. Animation by Konrad Polthier.
This fact inspired the mathematician Leo Moser to compose a limerick:
A mathematician named Klein Thought the Möbius band was divine. Said he: "If you glue The edges of two, You'll get a weird bottle like mine."
Some mathematicians really are multi-talented!
Another curious feature of the Klein bottle is that it intersects itself, which means it's hard to make it from a single tube of rubber as Klein suggested. Strictly speaking, the self-intersecting object depicted above isn't a Klein bottle, but (as Klein indicated) only a visualisation of one. To understand why, first think of the more familiar doughnut (known mathematically as a torus). You can make a torus from a square sheet of rubber by first gluing two opposite sides to form a cylinder, and then gluing the two boundary components of that cylinder to get the torus.

Making a torus: First glue opposite points on two opposite sides of the square to make a cylinder and then glue the two boundery circles of that cylinder (corresponding to gluing opposite points on the remaining two sides of the square) to form a torus.
If you don't want to bother with the gluing, you can simply think of the torus as a square, keeping in mind that opposite points on opposite sides are considered the same. So when you slide a shape drawn on the "square" across the top edge, it will re-appear at the bottom edge and when you slide it over the right edge it will re-appear at the left edge (and vice versa).
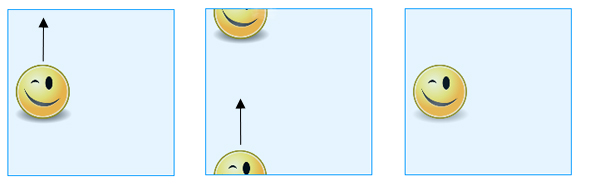
When you slide a shape drawn on the "square" across the top edge, it will re-appear at the bottom edge.
To get a true Klein bottle, start in the same way, identifying opposite points on a pair of opposite sides of a square. For the other pair of sides, however, don't identify points that are directly opposite, but points that are diagonally opposite, as shown in the picture.
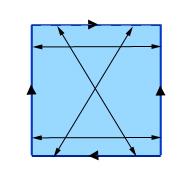
Making a Klein bottle: identify opposite points of two opposite sides (the vertical ones in this picture) and then identify diagonally opposite points on the remaining two sides. (If you label points on the top and bottom sides from left to right by the numbers 0 through 1, then a point with label x on the top side is identified with the point with label 1-x on the bottom side.)
The resulting object is the Klein bottle. Again, you can think of it as a square, keeping in mind which boundary points are considered the same. If you slide a shape over one of the edges that had opposite points identified (vertical in our picture), it reappears reappear on the opposite side, like before. If, however, you slide it over one of the edges whose points were identified diagonally (horizontal in our picture), it appears on the opposite side, but displaced and as a mirror image of its original self.
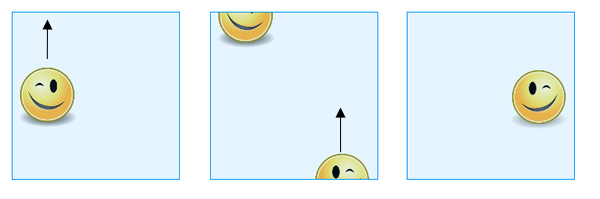
If you slide a shape over the top edge, it appears across the bottom edge, but over to the other side and as a mirror image of its original self.
The only way to build this shape in three-dimensional space by actually gluing points together is to allow it to intersect itself. This amounts to identifying pairs of points in the interior of the original square, so strictly speaking the resulting shape is not exactly the same as the Klein bottle, which only has boundary points identified. It's just one way of representing the bottle in three-dimensional space (there are others too).
Mirror image and orientability. Animation by Konrad Polthier.
Curiously, the concepts of "inside", "outside" and "one-sidedness" depend on the ambient space an object is sitting in. For example, a loop drawn on a piece of paper (in two-dimensional space) has a well defined inside and outside, but a loop drawn in three-dimensional space doesn't. This is why we can't talk about one-sidedness unless we first decide how to embed a surface in three-dimensional space. There is, however, a closely related property that is intrinsic to a shape and doesn't depend on the surrounding space. A surface is called orientable if you cannot slide a shape drawn on it around and back to where it started so that it looks like its own mirror image. As you can see in the animation accompanying the image on the right, the Möbius strip isn't orientable. And as you can see from the image with the smiley face above above, neither is the Klein bottle. To give it its full mathematical description, the Klein bottle is a closed, non-orientable surface. To find out more about it see the article Inside the Klein bottle.
About the author
Marianne Freiberger is Editor of Plus.