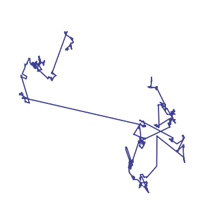
An example of a Lévy walk.
When dogs are let off leashes in parks they often display the same kind of behaviour. They'll thoroughly sniff out a small patch of grass, then dash madly off to somewhere else, sniff out a new patch, and so on. You might think it's sheer exuberance that makes them do it, but people have suggested that there's a reason: when an animal is searching for food that is randomly distributed throughout an area, but not too abundant, then this way of moving around may optimise its chance of finding it. Mathematicians call this kind of movement a Lévy walk: it's made up of many short, straight paths in random directions with the occasional long trajectory thrown in.
Until recently the Lévy walk behaviour had been studied in living things with some kind of intelligence, but now a team of scientists in South Korea has found that unintelligent organisms can do it too: molecular compounds within our bodies, which have no intelligence at all, also appear to use Lévy walks to find their destinations. The behaviour emerges all by itself, with nobody measuring time and distances.
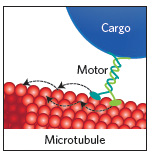
A molecular motor attached to a cargo and a microtubule.
The team looked at how so-called molecular motors transport various forms of cargo (called endosomes) through living cells. The molecular compounds carry their load along microtubules — tube-like structures that form a kind of highway network within a cell. It's possible, however, for all the motors that carry a cargo to detach themselves from a particular microtubule and reattach themselves to another one, thereby changing the direction they are travelling in. When the researchers analysed the paths taken by the molecular motors and their cargo through living mammalian cells, they found that they appear to be Lévy walks. The question is how those mindless motors, which have no memory or ways of measuring how far they have travelled in a particular direction, can follow such a distinctive pattern.
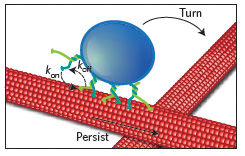
Motors can attach to a different microtubule and change direction.
where $m$ is some positive number, which for a Lévy walk is usually taken to lie between $1$ and $3$. You can see that, as $L$ gets larger, $P(L)$ becomes smaller. But because the exponent $m$ is at most $3,$ $P(L)$ doesn't become vanishingly small too quickly, so larger steps still do occur with a reasonable frequency. In most real-life situations extremely large steps (taking the dog out of the park or the cargo out of the cell) don't occur at all, which is why people look at \emph{truncated} power-law distributions, which have $P(L)=0$ for very large $L$, in these cases. It has been suggested that an exponent $m=2$ gives the optimal way of searching an area for targets that are randomly and sparsely distributed, but there is debate about whether that's really true.
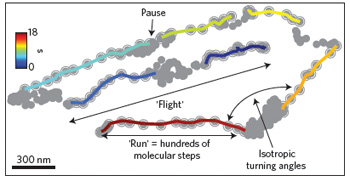
Each step of a Lévy walk also has a direction of course — when you look at the proportion $Q(D)$ of steps going into a particular direction $D,$ you find that this number is roughly the same for all directions: a Lévy walk doesn't favour one direction over another.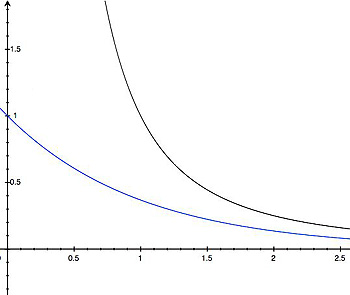
The black curve represents the power-law distribution P(L) = L-2 and the blue curve the exponential distribution P(L) = e-L. You can see that for larger values of L the former decreases more slowly than the latter: the power law distribution has what's called a "fat tail".
When molecular motors transport cargoes through a cell, their paths are made from little bursts of motion, called runs, punctuated by pauses. When the researchers analysed the lengths of individual runs, they found that these didn't follow a power law distribution at all. Instead, the frequency of runs decreased much faster with their length — exponentially in fact — so there weren't those long runs interspersed with the short ones that are characteristic of a Lévy walk. This exponential distribution of step sizes is more akin to what you would find when observing a mindless dust particle floating through the air randomly, describing what is called a Brownian motion. Brownian motion with an exponential step distribution has also been associated to foraging. People have claimed that it's the best way of looking for food that's abundant, which makes sense: when food is all around you, you don't need to dash off elsewhere during your search.
Both kinds of random paths — a Lévy walk and Brownian motion — can be simulated mathematically as a sort of random game. Before each step, choose the direction of the step at random with all directions being equally likely. Then choose the step length according to an exponential distribution for Brownian motion, and a power law for a Lévy walk.
This way of looking at things gives us a link between the two types of motion. It turns out that a "Brownian walker" can be turned into a "Lévy walker" simply by skewing the directional probabilities. If you start with a Brownian walk, but make the probability $Q(D)$ of choosing a particular direction $D$ larger if the walker has already moved in direction $D$ for some distance — so $Q(D)$ grows with the distance already travelled in direction $D$ — then you increase the chance of consecutive steps lining up and pointing the same way: the longer or more numerous the steps that have lined up already, the higher the chance of the next one lining up too — it's called \emph{self-enforced directionality}. If you count the lined-up steps as one long step, then the new distribution of step-lengths can end up following a power-law, so what you have is a Lévy walk.
This mathematical insight, so the South Korean team, delivers the reason why Lévy walks appear in living cells. In the team's model the transport of cargo along a microtubule is governed by two factors: on the one hand there is the number of motors on a cargo that are attached to a microtubule, and on the other there is an opposing force against which those motors have to struggle when moving the cargo (the force is due to factors such as drag). The load induced by the force is shared by all the motors attached to the microtubule, so the more of them there are, the easier it is for them to resist the force and hang on to the tubule.
Consecutive short runs can line up in the same direction, creating a Lévy walk.
If all the factors balance out just right, then this gives rise to self-enforced directionality: loosely speaking, the more of the motors on a cargo have had time to attach to a particular microtubule, the better they share the load and the slower the rate at which they get prized away by the force. This gives un-attached motors the time to attach to the same microtubule as well, so the chance for the transport to continue along that tubule in the same direction increases. Thus, the motion of the cargo, which might otherwise have been Brownian, turns into a Lévy walk because the motors win over the opposing force sufficiently many times to create the long trajectories characteristic of the Lévy pattern.
"Nature is more clever than we are," says Steve Granick, Director of the IBS Center for Soft and Living Matter, where the research was carried out, and co-author of the study. "It finds this efficient way to engineer this marvelous result without being smart, without (using any pre-existing) memory, and it saves energy. The findings of our study may help us to better understand our cells and how our body is engineered."
But there is also another potential benefit: if you know how Lévy walks can arise in mindless systems then you can also program artificial systems to produce them. The researcher think that the mechanism they discovered holds promise for the engineering of artificial active materials, which can react to stimuli, for example by changing their shape or colour, and have uses in many areas of science. The study has been published in the journal Nature Materials.
This article now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
