
We live in the information age. Most of what we do is hugely influenced by our access to massive amounts of data — whether this is through the Internet, on our computers, or on our mobile phones. The buzz word to describe this deluge of information is Big Data. In 2012 the UK government identified Big Data as one of the eight great technologies of the future. So what does the challenge of Big Data entail and how can we meet it?
Where does Big Data come from?
Perhaps the leading source of current Big Data is the Internet. According to a recent estimate, about 1021 bytes (a zettabyte) of information are added to the Internet every year, much of which is graphical in content. The internet penetration in the UK is over 80%, and in all but a few countries it is over 20%.
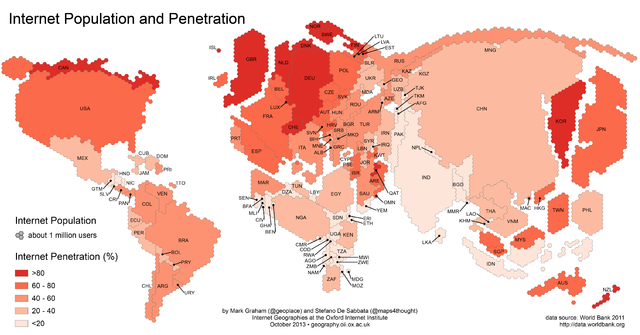
This map illustrates the total number of Internet users in a country as well as the percentage of the population that has Internet access in 2011. Image: Stefano De Sabbata and Mark Graham, CC BY 3.0.
A major source of this data is the ever growing content on social media websites. For example, Facebook was launched in 2004. It now has 2 billion registered users (about a quarter of the world's population!) of which 1.5 billion are active. Around 2.5 billion pieces of content (around 500 terabytes of information) are added every day to Facebook, with most of this data stored as pictures. The search engine Google is estimated to seek information from around 15 exabytes (1015 bytes) of data (which it searches using a clever mathematical algorithm).
Another source of Big Data are mobile and smart phones. There are now more mobile phones than people in the world, with the potential for 25,000,000,000,000,000,000 possible simultaneous conversations. The forthcoming plans for a 5G network will offer data rates at 1 gigabyte per second simultaneously to tens of workers on the same office floor. Another fast-approaching technology are sensors that can provide constant monitoring of, say, our state of health (with significant ethical implications). The 5G network will support several hundreds of thousands simultaneous connections for massive sensor deployments. Indeed the future is rapidly approaching: soon our devices will simply communicate with each other (for example the cooker talking to the dishwasher and also to the supermarket every time a meal is prepared) with little or no human interference — it's called the Internet of things.

Smart watches can give you up-to-date health information wherever you are.
Significant amounts of data, of significant interest to the social sciences, also come from the way that we use our devices and the information this gives about our lifestyles. Again there are significant ethical issues here. Every time we make a purchase on Amazon, use our bank on-line, switch on an electrical device, or simply use a mobile phone or write an email, we are creating data which contains information that can in principle be analysed. For example, our shopping habits can be determined, or our location tracked and recorded. Mathematics can be used at all stages of this, but we must never lose sight of the moral dimension in so doing.
The nature of Big Data
In one sense, Big Data has been the subject of mathematical investigation for at least 100 years. A classical example is meteorology, in which huge amounts of numbers need to be crunched to produce reliable weather forecasts. Similarly large data sets arise in climate models, geophysics and astronomy.
However, the data sets in these problems, while very large, are also well-structured and well-understood, with known levels of uncertainty. That's because they come from physical processes that, on the whole, scientists understand well. The real challenges of understanding and dealing with Big Data come from the biological sciences, the social sciences and in particular from people-based activity. Such data is often garbled, incomplete, unreliable, complex, anecdotal and fast-arriving. It is often qualitative rather than quantitative, it isn't homogeneous, and it's about relations between things, rather than the things themselves, in a way that physical data isn't.
What questions do we want to ask of Big Data?
How do we visualise Big Data, make speculations from it, model it, and understand it? How do we experiment on the systems that generate it, and ultimately how might we control those systems? The mathematical and scientific challenges behind these questions are as varied as they are important, and the very scale of Big Data makes automation necessary. This automation in turn relies on mathematical algorithms.
Questions we might ask from Big Data include:
- How do we rank information from vast networks in web browsers such as Google?
- How do we identify consumer preferences, loyalty or even sentiment and how do we make personalised recommendations?
- How do we model uncertainties in health trends for individual patients?
- How do we achieve and deal with real-time health monitoring (especially in the environment that 5G will lead to)?
- How to use smart data in energy supplies?
It is fair, I think, to say that many of the future advances in modern mathematics (together with theoretical computer science) will either be stimulated by the applications of Big Data or driven by the needs to understand Big Data. Many existing mathematical techniques (some of which until recently were considered as pure mathematics) are now finding significant applications in our understanding of Big Data. A key example of this is the mathematics of network theory.
Networks everywhere
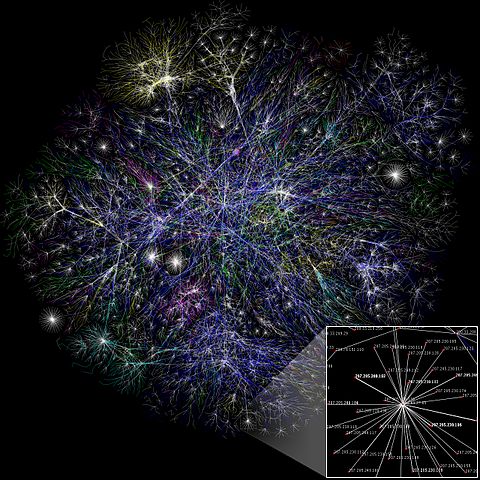
A partial map of the Internet based on 2005 data found on The Opte Project. CC BY 2.5.
As the name suggests, network theory describes objects, called nodes, that are linked together by what are called edges. The nodes could be computers or websites, and the edges connections between the computers or links between the websites. The nodes can also be people and the connections their friends on Facebook or Twitter, or they could be mobile hand sets and the links conversations or simply a close proximity which might lead to interference. Network theory explains the nature of networks, allows us to search for connections between individual points in data sets, and can describe the movement of information around a network. (You can read more about graphs and networks on Plus.)
Indeed, managing the mobile phone network (which is of course also used to download data) is a significant and growing application of the theory of graph colouring: finding ways of colouring the edges or nodes in a network according to specific constraints, such as adjacent nodes having to have different colours. For example, the colours might represent frequencies assigned to mobile phone transmitters, which have to be chosen to minimise interference and so need to be different for adjacent transmitters. Graph colouring was until recently regarded as belonging firmly in the domain of pure mathematics.
Other examples of networks which lead to big data include organisational networks (such as management networks, crime syndicates, even the voting behaviour in the Eurovision Song contest), technological networks (such as the power grid or electronic circuits), information networks (made up of genes, protein-protein interactions, word-of-mouth dissemination of information, myths and rumours), transport networks (such as airlines, food logistics, underground and overground rail systems), and ecological networks (food chains, diseases and infection mechanisms).
The power of network theory
Network theory can address many other questions related to Big Data. When you are dealing with very large networks it is not always easy to identify clusters — groups of nodes that are highly interlinked — or to segment the data into groups that share common features. Such information is vital in data mining and pattern recognition. It is especially relevant to the retail industry, who are interested in the behaviour and preferences of their customers, but can also be used to identify friendship groupings in social networks, to investigate the organisation of the brain, and even to finding voting patterns in the Eurovision Song contest. Network theory provides the algorithms both for identifying clusters and for segmenting data.

Information, gossip, infectious diseases: they all spread through social networks.
Such analysis can also help with another very significant problem encountered in many applications: linking data bases with different levels of granularity in space and time. An example is weather forecasting, where some of the data might be coming from satellites orbiting the Earth and transmitting MBytes of data a second. Other data might be from individuals in isolated ground stations who might only give a few measurements every day. Some of the data might even be historical such as records of sea captains 100 years ago. All three such data sets are useful and they have to be linked together in a seamless manner.
Equally important is the question of how connected a network is on the whole: are individual nodes connected to many others throughout the network, or are the connections sparse? What is the shortest path through the network? These questions are essential for efficient routing in the Internet, interpretation of logistic data, understanding the speed of word-of-mouth communications and even marketing. Network theory is also essential in searching for influential nodes in huge networks. Highly connected nodes — whether they represent people, websites, or airports — are hugely important for the robustness of a network, since removing them would significantly alter its overall connectedness. Such information can be used to break up terrorist organisations, stop epidemics from spreading, or keep air traffic rolling when a region is affected by bad weather.
What else can maths do?
Network theory is just one of a variety of mathematical techniques used to study Big Data. Much of Big Data takes the form of images, so mathematical algorithms that classify, interpret, analyse and compress images are extremely important. Statistical methods have long been used to analyse and interpret images, but there has recently been a significant growth in novel mathematical algorithms, drawing on ideas from pure mathematics people previously thought had no direct applications in the real world. Some of these algorithm are based on the analysis of complicated equations, leading to some powerful and unexpected applications of highly technical tools from the relevant theory of equations. Algebraic topology, an area of maths that investigates properties of shapes using algebra, plays a very useful role in classifying images. And techniques from category theory, an area that investigates mathematical structures and concepts on a highly abstract level, can be used to "parse" an image to see how the various components fit together. In the context of machine learning this allows for machines to "perceive" what the objects in an image are and to make "reasoned" decisions about it.
This is only a short list. There are many other areas of mathematics and computer science that have also found applications in the study of Big Data. So watch this space! I am confident that we will see great advances in pure, applied and computational maths arising from these challenges.
About the author

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.