
Power networks
A network picture of part of the internet, based on 2005 data. Image: The opte project.
Think of a network — any network. It could be a social network, the internet, the power grid, or a transport network. You can draw each of them on a piece of paper (in theory at least), using a dot to represent a node (a person, website, power station, etc) and a link between two nodes if they are, well, linked.
One thing you might want to know about such a network is the extent to which nodes are connected to other nodes. You could work out the average number of connections per node, but that's a bit crude. You could also produce a histogram: for each number $x,$ count the number $y$ of nodes that have $x$ connections. When people first started doing this, they noted a curious feature. The variable $y$ often follows a power law; that is, it is proportional to $\frac{1}{x^k},$ where the exponent $k$ is typically small, somewhere between $2$ and $4.$ When this happens the network is called scale free.Plotting the graphs of these functions (see below), you see that $y$ decreases as $x$ increases, which makes sense: you'd expect there to be fewer nodes with many links (highly popular people or websites, transport hubs, etc) than nodes with fewer links (less popular people, average websites or train stations, etc).
The same would be the case, however, if the number $y$ of nodes with $x$ links decreased exponentially with $x,$ rather than in this power law fashion. So why do we see power laws in so many different networks, rather than, for example, exponential distributions of links? In 1999 the mathematicians Albert-László Barabási and Réka Albert suggested an interesting answer to this question. They assumed that when it comes to networks, the rich tend to get richer — in other words, that new nodes joining the network are more likely to link up to nodes that already have many connections than to nodes with fewer connections. This assumption makes sense. When you write your blog, you are more likely to link to very popular sites, say the BBC news website, than obscure ones. And when you are planning to build a train station, you're more likely to connect it to a busy transport hub than to a small village.
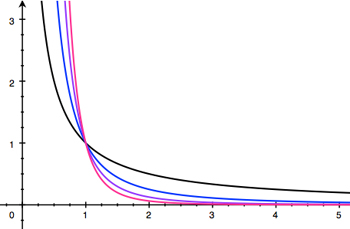
The plots for k = 1 (black), k = 2 (blue), k = 3 (purple) and k = 4 (pink).
Barabási and Albert investigated what happens if you build a network randomly, but with the probabilities of a new node attaching itself to existing nodes governed by the rich-get-richer rule — and they found that scale-freeness naturally emerges. It's therefore stands to reason that scale-freeness is a result of the rich getting richer, even in networks that are not, strictly speaking, random.
Being scale free can be good and bad at the same time. On the one hand, there are many nodes with relatively few connections. So if bad weather disables a random node in a scale free transport network, then this isn't necessarily such a disaster. Chances are that the node doesn't have too many connections, so its failure isn't going to effect the rest of the network too badly. On the other hand, it's not that highly connected nodes don't exist in a scale free network. If you are a terrorist trying to disrupt the network, you should try to take out one of them, disabling much of the network in an instant.
Where does the term scale free come from? Saying that a variable $y$ is proportional to $1/x^k$ means that there's a constant $c$ so that $$y = c \times \frac{1}{x^k}.$$ Suppose you want to know how the number $y$ of nodes with $x$ links changes as you double $x.$ From the formula, you see that $$c\frac{1}{(2x)^k} = \frac{c}{2^k}\times \frac{1}{x^k}.$$ In other words, the number $y$ with $x$ nodes changes by a factor of $1/2^k$ as you double $x.$ This is the case whether you double $x$ from $10$ to $20,$ or from $1,000,000$ to $2,000,000$ (a much larger gap). The proportional change in $y$ is always the same whether you're looking at really small intervals from $x$ to $2x,$ or at really large ones — it is independent of scale! You could also think of this in terms of units. Suppose you change your basic unit from counting individual links (represented by $x$) to counting them in lots of $100$ links — this is a bit like going from centimetres to metres in situations that involve length. When you rewrite the power law formula in terms of $z=100x$ you get $$c \times \frac{1}{x^k} = c \times \frac{1}{(z/100)^k} = 100^kc \times \frac{1}{z^k}.$$ The change of units means that you have to multiply the original expression by a corresponding factor ($100^k$), but it doesn't change the fact that $y$ is proportional to $1/x^k.$ As you change units by scaling $x$ you don't change the nature of the relationship. The relationship is free of a characteristic scale.About the author
Marianne Freiberger is Editor of Plus.
Comments
Anonymous
The sentence after the second equation "the number $y$ with $x$ nodes changes by a factor of $c/2^ k$" must read "the number $y$ with $x$ nodes changes by a factor of $1/2^ k$".
Marianne
Thanks for spotting the mistake, we have corrected it.
Anonymous
In our work we demonstrated the same in the semantics of an operating system.
http://www.complex-systems.com/abstracts/v23_i01_a04.html