
This article is part of the Finance and physics package. Click here to see the previous article in the series.
As we have seen in the previous article, formulating the theory of the weak force as a gauge theory leads to a problem: the gauge theory says there should be massless particles associated to the weak force, and such particles haven't been observed in nature.

Gold opens up a new opportunity to speculate.
But it turns out that there is a way around this problem. It is called the Higgs mechanism, and although it is named after the physicist Peter Higgs, it was actually proposed by many researchers too (you can find out more here).
Here we will explain it using the economic analogy. So far, we have assumed that you can only carry money between countries. Now, let us assume that you are also allowed to carry gold. Gold has a price in each country, which is set by the inhabitants of each country independently of the others. A savvy speculator realises that a new opportunity opens up. You can now buy gold in one country, take it to the next, sell it, and bring back the money to the first country. As an example, say that the exchange rate between Pesos and Dollars is 4 Pesos = 1 Dollar. And the price of gold in Argentina is 40 Pesos per ounce and the price in the USA is 5 Dollars per ounce. What would you do?
Think about it! Do not continue reading until you have the answer. It is a bit hard, but worth the effort!
You would start with five Dollars in the USA, buy gold there, go to Argentina, sell it for 40 Pesos, go back to the USA and get 10 Dollars when you cross the bridge back. This operation then has a gain of a factor of two, or a 100% profit.
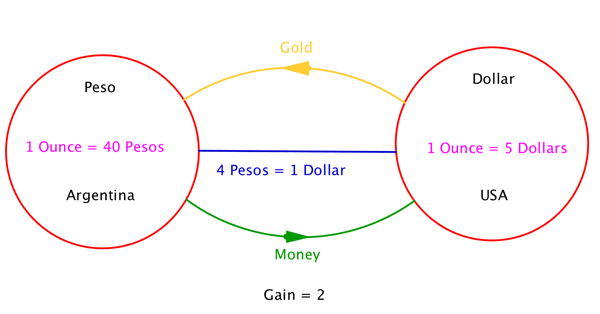
Here we see two countries with their respective gold prices. We have also given the exchange rate between them. For these prices and exchange rate it is possible to earn money by buying gold in the USA, taking it to Argentina, selling it there and bringing back the money, exchanging it at the bank, of course. The net gain is a factor of two or 100%. Gold is indicated in yellow and money in green.
Note that we continue to have the gauge symmetry. If the Argentinean government changes the currency to Australes your gain would be the same.
Now, we can use this gauge symmetry to choose the currency so that the price of gold is the same in all countries. Let us call the new units New Pesos and New Dollars. Now the price of gold is 1 New Peso per ounce and 1 New Dollar per ounce. However, the exchange rates might not be one to one. In fact, they cannot be one to one if originally there was an opportunity to speculate. For the example above the new exchange rate is 1 New Peso = 2 New Dollars. Note that this is not a "gold standard" that removes all exchange rates. It is very important that the exchange rates are still present.
In summary, now the new prices and exchange rates are
1 New Peso = 2 New Dollars 1 ounce = 1 New Peso 1 ounce = 1 New Dollar
If you are a speculator, now it is easier to see what to do, isn't it? With these new currency units obtained by setting the price of gold to 1 one can immediately see that if any exchange rate is different than one to one, then there is an opportunity to speculate by performing the gold circuit. The opportunity to speculate remains, and the gain remains a factor of two, or 100% profit. As usual, the net gain does not change when we change currency units.
Now let's go back to looking at a wave in our economic model. Let us first use a gauge transformation to set the price of gold to the be same in all countries. Now any exchange rate that is different than 1:1 will give rise to a speculative opportunity by running the gold circuit along that link, or bridge. It does not matter, whether the wavelength is long or short.
Therefore, the speculator's gain doesn't necessarily decrease with the wavelength. Once we set the price of gold to 1 everywhere, any exchange rate that is different from one to one leads to an opportunity to speculate.
In the physics version, this would mean that it now costs some energy to move any exchange rate away from one to one. This cost is present even for long wavelength configurations. In physics, this leads to a massive particle, to a massive photon. A mechanism of this sort is happening inside superconductors, and this was indeed an inspiration for the Higgs mechanism.

The massive Z and W bosons were discovered at the the Super Proton Synchrotron at CERN in the 1980s. Image © 1976-2016 CERN.
We think that a similar mechanism gives mass to the particles related to the weak force. At each spacetime point (country) there is some object (the analogue of gold) that has some orientation in the weak sphere. The details are more complicated because the symmetries correspond to rotations, and we will not describe it here. Essentially, the presence of this object means that the cost of exciting waves does not go to zero as the wavelength tends to zero. And this in turn means that the particles associated to the waves in the weak force field have a non-zero mass.
If one sets the price of gold to one everywhere, then one is not free to do gauge transformations to further modify exchange rates. For this reason people sometimes say that the gauge symmetry is broken. This is conceptually misleading because the gauge symmetry is still present, if we remember that we need to also change the price of gold.
There is one interesting fact we have neglected to tell you so far. Photons and the corresponding particles for the weak force actually mediate the respective forces. When particles interact through these forces, it's by exchanging mediator particles. For electromagnetism the mediator is the photon, and for the weak force the mediators are the massive W+, W- and Z bosons. All of these have been observed in experiments.
Quantum mechanics
The system we have described so far, through the economic analogy, gives rise to what is normally called a classical field theory. A field is a quantity that is defined at each point in spacetime. For example, the price of gold is a field; at each point in spacetime it takes a definite value. Similarly, the exchange rates are also fields. For each point, we have one exchange rate per spacetime dimension, since the number of neighbours that a country has is proportional to the dimension of spacetime.
But this is not the whole story. The dynamics of these fields is ruled by the laws of quantum mechanics. An important feature for these laws is that they are probabilistic — they depend, to some extent, on chance. One might think that in the vacuum, when there aren't any particles around, all the fields are zero. However, this is not the case, they take random values. All we can say is that they are given by a certain probability distribution. In the economic analogy, we can say that the values of the exchange rates and the price of gold, are all random. This randomness follows a very precise law, which is encoded in the precise form of the probability distribution. We will not give the precise formula here (it can be found in the appendix), but we simply note that it is such that configurations of exchange rates and gold prices become less probable when there are greater opportunities to speculate. We have a precise law for the probability of each configuration, but we cannot predict with certainty, which of the possible configurations will occur when we look at the system.
Note that all these fluctuations happen at short distances. If we follow a very big circuit, then we pass through many countries and their exchange rates all average out. In the vacuum, at long distance they average out to zero so that we recover the classical result where the fields are all zero.
The probability cost that we have to pay when we set the exchange rates to values leading to larger speculative opportunities is also related to the energy cost we discussed above. They are essentially the same. Higher energy configurations are less probable. In nature, the W+, W- and Z bosons that carry the weak force are very massive. They weigh around a hundred times the mass of the proton, which is a lot for an elementary particle. Their large mass explains the weakness of the weak force. It implies that we are very unlikely to produce fluctuations in the "weak exchange rates". Therefore, a particle that interacts only through the weak force, such as the neutrino, is very difficult to see. In fact, a few per cent of the energy of the Sun comes out in neutrinos (this shows that the weak force is important for the workings of the Sun.) However, we are totally oblivious to these neutrinos. They simply pass through us day and night and we do not see them. You need very big detectors with very sensitive electronics to catch a very tiny fraction of them. (You can find out more in Mysterious neutrons.)
The mechanism described above does give a mass to the mediators of the weak force, but it does not explain why there should be a new physical particle, such as the Higgs boson. This is what we will look at next.
Previous article: The weak force and massive particles Next article: The Higgs boson
Back to the Finance and physics package
These articles contribute to our Stuff happens: The physics of events project.
About the author

Juan Maldacena is the Carl Feinberg professor at the Institute for Advanced Study at Princeton, New Jersey, USA. He works on quantum field theory and quantum gravity and has proposed a connection between those two (see this article).