Out of all the regular polygons there are only three you can use to tile
a wall with: the square, the equilateral triangle, and the regular
hexagon. All the others just won't fit together.
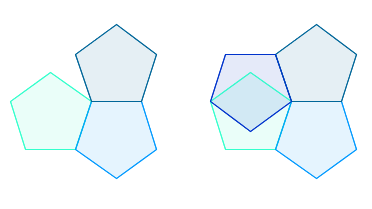
Trying to fit pentagons around a point.
It's quite easy to prove this. A regular polygon with $n$ sides
has interior angles of
$180\frac{n-2}{n} \mbox{ degrees.}$
Suppose you try and make a tiling by fitting several copies, say $k$
of them, around a point so that they all meet at a corner (see the image
above). Then the $k$ angles must add up to 360 degrees. If they
add up to less there will be a gap, and if they add up to more then
copies of the polygon will overlap.
So we need
$$k \times 180\frac{n-2}{n} = 360,$$
which means that
$$ k = \frac{2n}{n-2}.$$
The term on the right hand side can be rewritten to give
$$ k = \frac{4}{n-2}+2.$$
Since $k$ is a whole number (the number of copies of the polygon
you are fitting together), this means that $4/(n-2)$ must also be
a whole number. Therefore $n-2$ can only be equal to 4, 2, and 1,
which means that $n$ can only be equal to 6, 4, and 3.
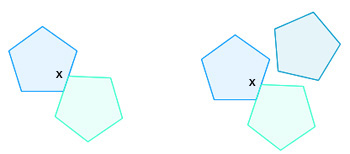
Trying to fit a third polygon with two copies offset against each other.
You could also try to make a tiling in which a corner of the polygon
does not necessarily meet the corner of a neighbouring copy, but sits at
some point $x$ along the neighbouring copy's side. That
neighbouring copy would therefore have an interior angle of 180 degrees
at $x$ (since $x$ is in the interior of one of its sides).
To make a tiling you would have to fill the remaining 180 degrees with $k$
copies of the polygon, so you would need
$$k \times 180 \frac{n-2}{n} = 180.$$
Using a similar argument as above you can convince yourself that this only works when $n=3$ or $n=4.$
You can read more about tilings on
Plus.
Return to the Plus advent calendar 2016.
This article comes from our Maths in a minute library.


