The harmonic series look simple. But, perhaps breaking your intuition, grows without bound!

The surprising physics of stacking coins.

We explore a famous problem which shaped 20th century topology. 

How can statistics help us to make informed decisions. Find out with this brief explanation of hypothesis testing?

What are mathematical invariants and why are they useful?

A lattice may seem like a simple regular grid of points, but it leads to fascinating new research in maths and cryptography!

Ingenious maths keeps your credit card details safe when you shop online and underlies the security of the internet.  Find out how in this easy introduction.

Whenever you smell the lovely smell of fresh coffee or drop a tea bag into hot water you're benefiting from diffusion. Find a quick introduction to the concept here.

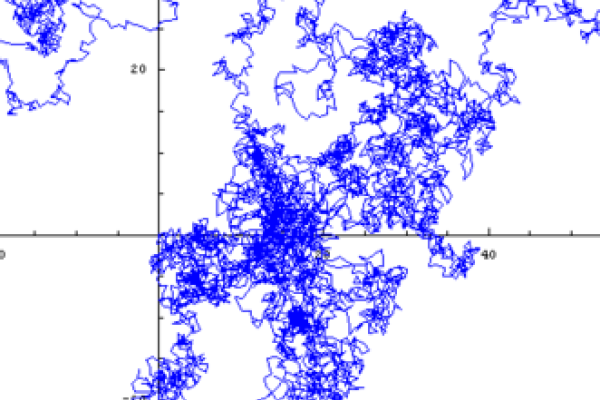
Random walks are great for modelling anything that moves, from particles to people. They're also fun, versatile and beautiful!

Even simple rules can lead to interesting processes. Play with Conway's famous cellular automaton to see life-like patterns unfold. 

Worried about your population of bugs? A branching process can help you understand it.