
Image: Royal Mint.
In March 2017 a brand new £1 coin will arrive in our purses. It's been designed to be harder to counterfeit than current coins, one in thirty of which are believed to be fake, but it's also been predicted to cause trouble. Businesses throughout the country are being urged to check whether their cash handling equipment — vending machines or automatic check-outs for example — can handle the new coin, and may have to update their machines. The cost to industry will be large. Even just replacing parking meters is likely to cost around £50 million.
So what's the problem? One feature of the new coin is that it's twelve-sided, rather than round. It's not the first non-round coin in circulation — 20p and 50p coins are seven-sided — but it'll be the first with a variable width. This means that it won't roll as well as other coins, a fact that some people fear will cause problems in cash handling equipment. The trouble is that twelve is even while seven is odd.
Why does the number of sides make a difference? To measure the width of a 2D shape, like a coin, place it between two parallel rulers so that each ruler touches the shape. The distance between the two rulers is the width of the shape — if you were to drop the shape into a slot, the slot would have to be at least that wide for the shape to fit through.

When your shape is a circle, as the coin above, the width you measure doesn't depend on where exactly the rulers touch the shape. You can see this in the Geogebra applet below. Drag the red point around the circle to see how the width remains the same as you change the points the rulers touch, which also alters the orientation of the rulers.
If your shape isn't a circle, however, the width usually does depend on the orientation of the rulers. The following applet shows this clearly for the example of an ellipse. The circle is a shape of constant width, but the ellipse isn't.
It's hard to imagine a non-circular shape with constant width, but these shapes do exist. An example is the Reuleaux triangle. Start with an equilateral triangle and stick the needle of a compass into one of its corners. Now draw a circular arc connecting the two other points, as shown in the picture below. The radius of this arc will be the length of the triangle's sides. Repeat for the other two corners to get a triangle with curved sides.
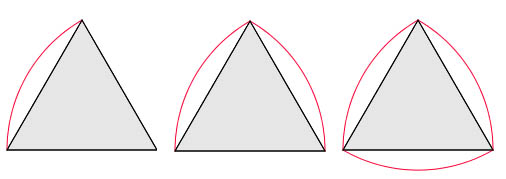
A Reuleaux triangle
It's hard to believe, but the resulting shape has constant width. If you were to trap the Reuleaux triangle between two rulers, one of the rulers would always touch a corner of the triangle and the other the opposing arc. The distance between the rulers would then be the radius of the circular arc, which is the same for all three arcs. If you need further convincing, look at the video below, featuring a roller whose wheels, in cross section, are Reuleaux triangles. The roller itself appears to have a bumpy ride, but the glass plate placed on top glides along smoothly, parallel to the surface below. That's because the width of the wheels, which is the distance between glass plate and surface, remains constant throughout.
Bermuda has (rather fittingly) produced a coin in the shape of a Reuleaux triangle:

Image courtesy Dale Hathaway.
In the UK there aren't any triangular coins in circulation, but a similar technique as the one that creates the Reuleaux triangle also works for the seven-sided heptagon the 20p and 50p coins are based on — in fact it works for any regular polygon with an odd number of sides. Prick the needle of a compass into one of the corner points and then draw a circular arc connecting the end points of the opposite edge. The resulting shape has constant width. In the image below, we have drawn the full circles, rather than just the arcs that form the sides, as this gives a prettier picture.
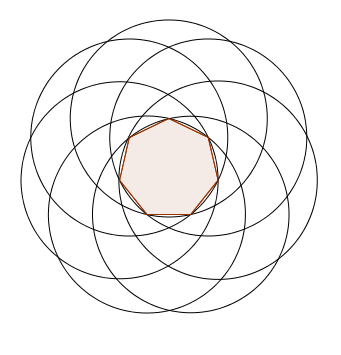

For an even-sided polygon, the technique doesn't work because a corner point doesn't lie opposite an edge, but opposite another corner point. If you wanted to replace the sides of the polygon by circular arcs in a way that retains the symmetry of the polygon, the centres of the corresponding circles would have to lie on the lines that connect the midpoints of opposing sides. You can see this below for the example of a hexagon, which has six sides.
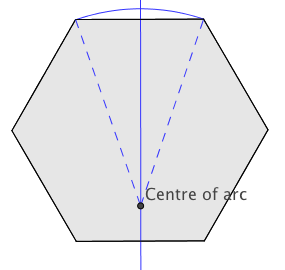
It turns out that this only gives a shape of constant width if all those midpoints are one and the same point right at the centre of the polygon. The arcs then join up to form a perfect circle: a good shape for a coin, but not what we were after here. You can explore this in the applet below for the example of a hexagon. Use the slider to move up the centre of the arc that forms the top horizontal slide.
Accordingly, the new £1 coin with its 12 sides has a variable width, between 23.03mm and 23.43mm. Whether this small difference will cause trouble in machines remains to be seen. Perhaps we can all look forward to a period of non-functioning parking meters.