Maths in a minute: The golden ratio
The golden ratio was first studied by the ancient Greeks, and it was defined in terms of geometry. Take a piece of line and divide it into a longer and a shorter piece so that the ratio between the whole piece and the longer piece is the same as the ratio between the longer piece and the shorter piece.
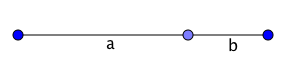
Divide the line so that the ratio between the whole line (a+b) and the longer piece (a) is equal to the ratio between the longer piece (a) and the shorter piece (b).
Let’s write 
for that ratio. We can work out the value of quite easily. Suppose that after the division the longer piece of line has length 
and the shorter one has length 
. Then, since equals the ratio between whole line and as well as the ratio between and , we get
![\[ \frac{a+b}{a} = \frac{a}{b} = \phi . \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0004.png) |
The left hand side of the equation can be written as
![\[ 1+\frac{b}{a}, \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0005.png) |
and since
![\[ \frac{b}{a} =\frac{1}{\frac{a}{b}} = \frac{1}{\phi }, \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0006.png) |
we have
![\[ 1+ \frac{1}{\phi } = \phi . \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0007.png) |
Multiplying through by gives
![\[ \phi + 1 = \phi ^2. \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0008.png) |
Using the quadratic formula to solve this equation we get a positive root
![\[ \phi = \frac{1+\sqrt{5}}{2} = 1.61803.... \]](/MI/7e4145c0fb311212cbd7eea6d68ce03d/images/img-0009.png) |
The golden ratio has all sorts of interesting properties, but perhaps the most famous one is its link to the Fibonacci sequence.
This famous sequence of numbers starts with two 1s. Subsequent numbers are formed by adding the two previous ones. This gives
![\[ 1,1,2,3,5,8,13,21,34,55,89,.... \]](/MI/da5fb43e790118bf34dda5811329c58d/images/img-0001.png) |
The sequence can be continued indefinitely. You can form a new sequence by dividing each number in the Fibonacci sequence by the number that came before:
![\[ 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, .... \]](/MI/9f551994997185e6b517442e1d20a725/images/img-0001.png) |
Here's a picture of this sequence:
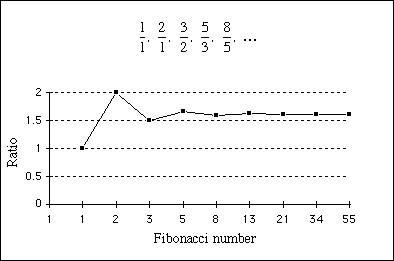
Ratio of successive Fibonacci terms.
You can see that, as you move down the sequence, the numbers approach a limiting value. And that limiting value is exactly the golden ratio!
To find out more about the Fibonacci sequence and the golden ratio, including their appearance in nature and supposed link to aesthetics, see this selection of articles.