
"I have not trodden through the conventional regular course which is followed in a university course, but I am striking out a new path for myself. "

Srinivasa Ramanujan (1887 - 1920).
This is what Srinivasa Ramanujan wrote in a letter introducing himself to the famous and esteemed British mathematician G. H. Hardy, in January 1913. Ramanujan was a self-taught mathematician working as a clerk in a post office in India when he wrote to Hardy at the University of Cambridge. What happened next became an inspiring tale of how an untrained genius could become accepted as one of the greatest mathematical minds of his time. Hardy invited Ramanujan to Cambridge, and on March 17, 1914 Ramanujan set sail for England to start one of the most fascinating collaborations in the history of maths.
"Ramanujan is a role model for the possible," says Ken Ono, the Asa Griggs Candler Professor of Mathematics and Computer Science at Emory University and also an advisor and associate producer on the recent film about Ramanujan, The man who knew infinity. "[His story shows] that you can come from impossibly difficult conditions or circumstances and become important. But he needed help, he needed Hardy. And Hardy wasn't the perfect mentor, he was a curmudgeon, he didn't like people. But through his help all of this happened."
When Ramanujan arrived in England he worked with Hardy on a range of mathematical topics. He arrived with little formal training, and had devised his very own way of writing mathematics that other mathematicians had never seen before.

The certificate of Ramanujan's nomination to become a Fellow of the Royal Society. Click here to see a larger image.
"Ramanujan didn't use the notation that everyone else in the world used," says Ono. "When he arrived here in England he knew nothing of modern mathematics. He made mistakes all the time." Ramanujan quickly learned a great deal of formal mathematics at Cambridge and went from an amateur to writing world class mathematics papers. "Very quickly, within the span of a year or two, he was formally trained. He was very smart so he could catch up quickly. The papers he wrote here [in England], by every professional standard, were world class papers. So that is also a testament to how gifted he was."
One of these papers, written with Hardy, astonished the mathematical community as it gave a way to reliably calculate numbers that had eluded mathematicians for centuries – partition numbers. This paper was one of those quoted in his nomination to be elected as a Fellow of the Royals Society, a high honour for any scientist. His nomination was signed by some of the great mathematicians of the day: including J. E. Littlewood, Alfred Whitehead, along with Hardy and many others. Ramanujan was elected a Fellow of the Royal Society on 2 May 1918 at the age of just 30, one of the youngest ever fellows elected. We spoke to Ono about the remarkable mathematical contributions of Ramanujan at the celebration of this centenary at the Royal Society, which he helped to organise (you can listen to a podcast of the interview here).
Partition numbers
The concept of partition numbers is quite straightforward. You can write any natural number as a sum of natural numbers. For example $3$ can be written as a sum in three different ways: $$ \begin{array}{rcl} 3& =&3 \\ 3& =&2+1 \\ 3& =&1+1+1 \end{array} $$ The number $4$ can be written as a sum in five different ways: $$ \begin{array}{rcl} 4&=&4 \\ 4&=&3+1 \\ 4&=&2+2 \\ 4&=&2+1+1 \\ 4&=&1+1+1+1 \end{Array}$$ The partition number $P(n)$ of a number $n$ is precisely the number of ways it can be written as a sum of natural numbers (without worrying about the order in which they are added). As we have just seen, $P(3)=3$ and $P(4)=5$. Writing down and counting the number of ways you can write a number $n$ as a sum seems easy, but in fact it quickly gets out of hand as $n$ gets large. You can probably work out for yourself that $P(5)=7$ and $P(6) =11$, but go any further than this and you will quickly run out of paper. The table below shows the partition numbers up to $P(10) =42$ which is already surprisingly large.
|
|
Looking at the graph of $P(n)$ for $n$ up to $10$ suggests the partition number grows exponentially with $n$.
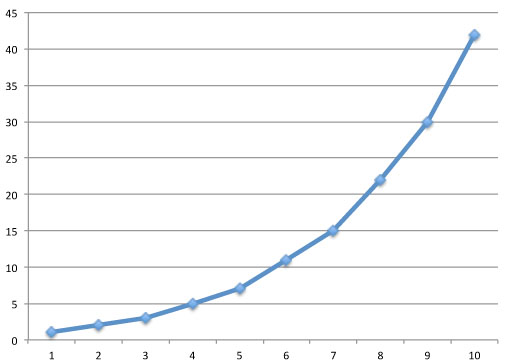
Partition numbers for n from 1 up 1o 10.
This fact led mathematicians to ask if there was a way of calculating $P(n)$ without having to explicitly write down and count up each way of writing $n$ as a sum. When studying this question Hardy and Ramanujan worked with the impressive "human calculator" Percy MacMahon who calculated tables of partition numbers for a great many numbers. Although those tables appear without rhyme or reason at first sight, Ramanujan noticed intriguing patterns in them. He spotted, and later proved, that the partition number for $4$, $9$, $14$, ... or for any number of the form $n=5k+4$ is always divisible by $5.$ Similarly, the partition number for any number of the form $n=7k+5$ is divisible by $7$, and for any number of the form $n=11k+6$ is divisible by $11$. These patterns are now famous as Ramanujan's congruences.
What gained Ramanujan the Royal Society Fellowship was the \emph{asymptotic formula} for the partition number he found together with Hardy. The formula doesn't give the precise value of $P(n)$, but it comes very close. And as $n$ gets larger, the difference between $P(n)$ and the asymptotic formula becomes arbitrarily small.
The formula is $$ P(n) \approx \frac{1}{4n\sqrt3}e^{\pi \sqrt{2n/3}} $$ Hardy and Ramanujan checked the value $w(n)$ given by the right-hand side of their formula against the values of $P(n)$ as calculated by their friend MacMahon:| n | P(n) | w(n) | w(n)/P(n) |
|---|---|---|---|
| 10 | 42 | 48.104 | 1.145 |
| 20 | 627 | 692.385 | 1.104 |
| 50 | 204226 | 217590.499 | 1.065 |
| 80 | 15796476 | 16606781.567 | 1.051 |
| 100 | 190569292 | 190569291.996 | 0.99999999997901 |
| 200 | 3,972,999,029,388 | 3,972,999,029,388.004 | 1.000000000000001 |
As you can see, the formula does what we promised. "It holds for all $n$. You can just plug in for $n$ and you basically get back the answer," says Ono. "Someone has to be pretty crazy smart to figure out a shortcut so you never had to count."
"At the time [the result] was considered an impenetrable problem. I'm pretty certain that that formula alone formed most of the citation for his election," says Ono. "But make no mistake that formula is now a very small part of what has grown to be [Ramanujan's mathematical] legacy."
Ken Ono.
And the legacy is indeed impressive: Ramanujan's work is today relevant in areas as diverse as computer science, electrical engineering, and physics, as well as, of course, mathematics. "Ramanujan's formulas have offered glimpses of theories that Ramanujan probably wouldn't have been able to articulate himself," says Ono. "Theories that nobody needed — until they needed them. For example [some work on black holes] makes use of some of Ramanujan's mathematics. Nobody even knew that black holes were something to study when Ramanujan was alive. But he had already developed some of the first formulas that would be used to explain their properties. What's astonishing is that Ramanujan has done this for us several dozen times."
"Where does this genius come from? I don't use the word genius very easily, but make no mistake — if you write down formulas that you find beautiful and important for some reason, and nobody knows why those formulas are important until decades later [...] that's something quite spiritual."
Ono is also Head of the Spirit of Ramanujan programme which supports emerging engineers, mathematicians and scientists, particularly those who, like Ramanujan, lack traditional institutional support. You can find put more about the programme here.
About this article
Rachel Thomas is Editor of Plus. She interviewed Ken Ono at the Royal Society's celebration of the centenary of Ramanujan's election as a Fellow of the Royal Society. You can listen to a podcast of the interview here.