
At every given point in time there are two points on the equator of the Earth that have the same temperature.
How do we know this? Well, here's a proof. Let's look at the equatorial plane which slices through the Earth at the equator. The equator is a circle which lies in that plane, and we can choose a coordinate system on the plane so that the point $(0,0)$ lies at the centre of the equator. For each point $x$ on the equatorial circle there is a point $-x$ which lies diametrically opposite $x$.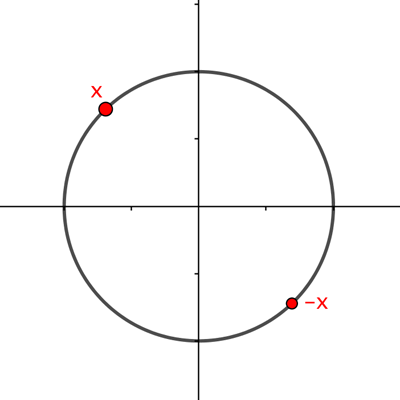
Points x and -x.
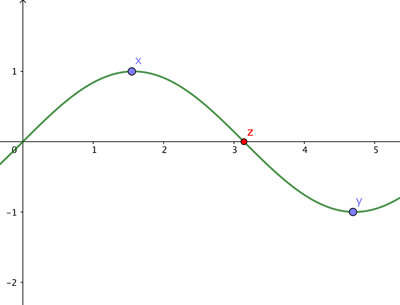
Illustration of the intermediate value theorem. If t(x)>0 and t(y) and t is continuous, then there is a point z between x and y such that t(z)=0.
Thus, since $f(-x)0$, there must be a point $y$ on the circle such that $f(y)=0$. So $$f(y) = t(y)-t(-y)=0$$ which means that $$t(y)=t(-y).$$ So the temperature at the point $y$ is the same as the temperature at the point $-y.$The result actually holds for any circle on the Earth, not just the equator. In fact, the result is the one-dimensional case of the Borsuk-Ulam theorem, which says that for any continuous function $t$ from the circle to the real numbers there is a point $x$ such that $t(x)=t(-x).$
The more general version of the Borsuk-Ulam theorem says that for any continuous function $t$ from the $n$-sphere to the set of $n$-tuples of real numbers there is a point $x$ such that $t(x)=t(-x)$.Read more about...