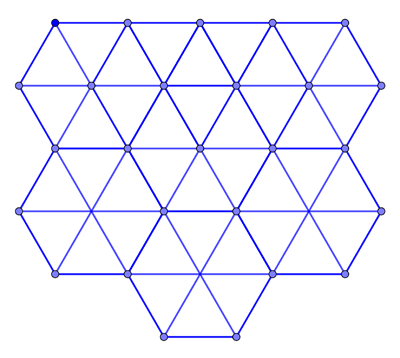
Imagine lots of people in a park, sitting in the Sun. Each person wants to keep at least 2m distance to everyone else, but they want to have as many people as possible at the minimum 2m distance. How should the people arrange themselves to make this happen? And what's the number of people a person will have exactly 2m away from themselves in this arrangement?

Let's start with a single person whom we will call person A. People who want to be 2m away from person A should position themselves somewhere on the circle that has A as its centre and a radius of 2. Let's look at two people on this circle, B and C. Since B and C also want to be 2m away from each other, the triangle formed by A, B and C should be an equilateral triangle with side length 2.

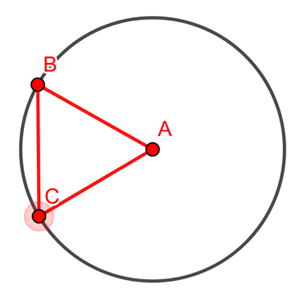
How many such triangles can you fit around A so that they don't overlap? Well, the angles in an equilateral triangle are all 60 degrees. There are a total of 360 degrees available around A, which means that you can fit exactly 360/60=6 equilateral triangle around A. In other words, the number of people that can position themselves 2m away from A and also be 2m from each of their two neighbours on the circle is six.

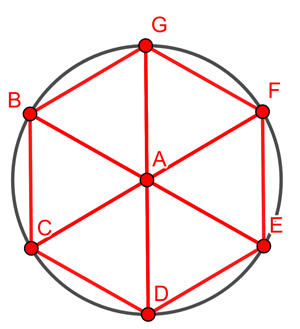
Now exactly the same argument holds for any other person on A's circle. The number of its closest neighbours, exactly 2m away is six, and they should be positioned around the person in the shape of a regular hexagon made up of six equilateral triangles.

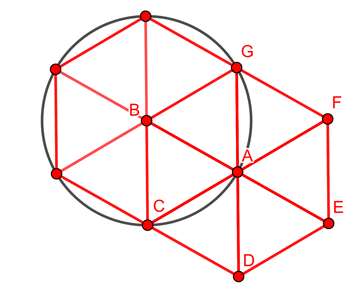
Since this works for every person the answer is that people should arrange themselves on a triangular lattice made up of equilateral triangles. Every person in the lattice is also at the centre of a regular hexagon.