In the first part of this article we found triangular numbers within the first large square in the complement of the blue grid.

Given that every square in the multiplication table is related to every other square (by multiplication or addition) it stands to reason that triangular also numbers feature in all of the other large squares in the complement of the blue grid. To see if they do, let’s look again at the multiplication table for 3 (so ). For now let’s focus on the top row of large squares, and start with the second large square from the left.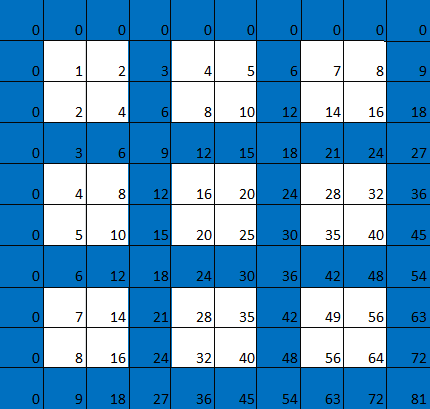

The sum of the numbers within that square is

So that’s 3 times the sum of the numbers in the first white square. Now look at the third white square from the left. The sum of the numbers within that square is

So that’s 5 times the sum of the numbers in the first white square. If you look at the fourth white square from the left, you will find that the numbers within it sum to 7 times the sum of the numbers in the first white square.

Off to the right more generally

Again we begin to see a pattern: the numbers in the large square from the left appear to add to the odd number times the sum of the numbers in the first square. The odd number can be written as and the numbers in the first square add to , so we are claiming that the sum of the numbers within the square from the left is

To prove this, focus on the first row of numbers in the square from the left. These are just the numbers in the top row of the first square (1 and 2) shifted along by In other words, the numbers are and

The numbers in the second row of the square from the left are equal to 2 times the numbers in the first row, so they are and

Adding up all the numbers in the square from the left gives

This is exactly what we wanted to prove.

The analogous result is true for the multiplication table which has multiples of coloured blue, for any positive integer We will leave it up to you to prove it, but if you get stuck you can see our proof here. Hint: In your proof you will have to deal with the sum of the first integers — and for this is handy to know that there's a neat formula for that sum:

Going down

What about the other large squares in the complement of the blue grid, the ones that don’t lie in the first row of large squares? Noticing that there’s a lot of symmetry in the multiplication table, we can hazard a wild guess. Perhaps the sum of the numbers in the large square that’s from the left from from the top is

where is the triangular number?

Let’s check if that’s true for , so

We start with the square that’s third from the left and third from the top. The numbers in this square are giving the sum

In this case so our guess turns out to be true.

Now let’s look at the square that’s third from the left and fourth from the top. The numbers here are which add to

Since now and our guess turns out to be true again.

It's possible to prove that the guess is true in general, not only for , but for all positive integers . We have already encountered the main ideas needed for the proofs, so you can have a go yourself. Or, if you prefer, you can see the proof here.

We have shown that triangular numbers don’t just occur in triangles, but also hide away within the square grid of the multiplication table. Given a triangular number you can find it (or rather its square) in the multiplication table which has multiples of coloured in. And doesn’t just turn up once in this table: every one of the large squares that make up the pattern contains a multiple of . To find out what multiple it is, you simply count what column and row the square in question belongs to.

We hope you have enjoyed this little journey through the secrets of the multiplication table!

About this article

Zoheir Barka, from Laghouat in Algeria, is an amateur and self-educated mathematician. He has a Masters degree in French language from Laghouat University and is currently a French teacher in elementary school.