
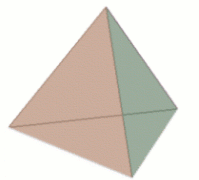
A 3-simplex, otherwise known as a tetrahedron. It has four face, each is a 2-simplex. In a similar way the "faces" of a 2-simplex (a triangle) are 1-simplices (line segments). In this way you build higher dimensional simplices from lower dimensional simplices.
If you love triangles as much as we do, we have great news – you can have them in any dimension you want!
Two-dimensional triangles can be generalised to 0 dimensions, 1 dimension, 3 dimensions or indeed to any number of dimension. Such a generalisation is called a simplex. A 0-simplex is a point, 1-simplex is a line segment, a 2-simplex is a triangle, a 3-simplex is a tetrahedron, a 4-simplex is a pentatope (a four-dimensional object whose five faces are tetrahedrons – don't worry we can't visualise it either), and so on. And these simplices are used to describe and understand different mathematical spaces.
Any two-dimensional space or shape can be built out of 2-simplices (ie, triangles) and these mathematical triangulations adhere to certain rules: the triangles meet either corner to corner or whole edge to whole edge, and they never share more than two corners or one edge. This means you can trace a line of edges in your triangulation, which is itself a triangulation of a 1-dimensional space (a line).

A geodesic sphere
A geodesic sphere is a triangulation of the two-dimensional surface of a sphere. It's true that with its flat surfaces it doesn't look exactly like a sphere, but they are the same in a certain mathematical sense.
Two objects are topologically the same if you can bend, stretch or shrink one into the other without cutting or tearing the object. The classic example is that a coffee cup is the same, topologically speaking, as a donut. Dent one side of your donut, making the dent bigger and bigger until it resembles the coffee cup and shrink the rest of the donut to become the cup's handle. On the other hand, to turn a ball into a donut you'd have to make a hole, something not allowed in topology. So a ball and a donut (or coffee cup) are not topologically the same.

CGI images start off as a mesh of millions and millions of shaded triangles. (Image by Headus, you can read more about the maths behind there work here.)
In this topological sense our geodesic dome is the same as a sphere: you just flatten the curved surface or push out the flat faces to transform from one to the other, all perfectly legitimate in topology. Similarly we can triangulate really complicated surfaces, such as the skin of the killeroo in the image above, or even something stranger like a one-sided Möbius strip.
We know that we can triangulate the vast majority of two-dimensional surfaces because of mathematical techniques developed over the last century. Tibor Radó was a Hungarian soldier who began studying mathematics when he was taken prisoner by the Russians in the First World War. He was taught by fellow prisoner and research mathematician, Eduard Helly. After Radó's escape from the Siberian prison camp, helped by Yupiks (indigenous people of Siberia) as he made his way through the Arctic regions of Russia, he became a professional mathematician. In 1925 he showed that it is possible to triangulate all two-dimensional surfaces you're ever likely to come across.
Triangulations are essential in the story of topology. From a triangulation you can calculate a vital piece of topological information about a surface: its Euler characteristic. This is the number V - E + F where V is the number of vertices (or 0-simplices), E is the number of edges (or 1-simplices) and F is the number of faces (in the case of a triangulation, the faces are 2-simplices). If two objects are topologically the same then they will also have the same Euler characteristic.
You can explore higher-dimensional spaces in this way too. A theorem, similar to Radó's result for two-dimensional surfaces, says that all three-dimensional surfaces can be triangulated using 3-simplices (tetrahedra). These triangulations of three-dimensional surfaces also have an equivalent Euler characteristic: V - E + F - T where T is the number of tetrahedra in the triangulation. From this we can see how we can generalise Euler's characteristic to any dimension, alternately adding and subtracting the number of 0-simplices (corners), 1-simplices (edges), 2-simplices (faces), 3-simplices and so on.
While two surfaces that are topologically equivalent have the same Euler characteristic, having the same Euler characteristic is not quite enough to guarantee that two shapes are topologically the same. To completely pin down the topology of a surface you need a little more information, for example whether it is one-sided, like the Möbius strip, or whether it has an inside and an outside like a sphere.
You can read more about topology on Plus, including its beginnings in the bridges of Königsberg. You can also read more about the Euler characteristic , about our favourite shape, and find out what other exciting places it can take you to.