
Non-linear relationships are tricky relationships. To understand why, let's first look at a linear relationship.
Imagine you want to buy a piece of string. The string costs 2 pounds per metre, so if you buy $x$ metres you pay $2x$ pounds. The relationship between the price $p(x)$ and the length $x$ is given by $$p(x)=2x.$$
This relationship between the length of string, $x$, and the price, $p(x)$, is called \emph{linear} because when you plot $p(x)$ against $x$ you get a straight line. (Equivalently, the equation or function describing this relationship are also called linear.)
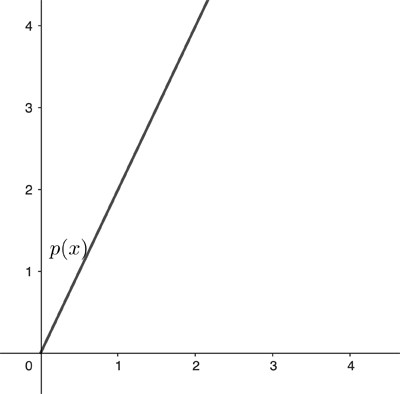
The relationship is pretty straightforward. For example, it's easy to see whether you can afford to increase the length of string by $a$ metres. The increase in price would simply be twice the increase in length, irrespective on the original length $x.$ You can see this using the equation: $$p(x+a)=2(x+a) = 2x+2a.$$
In this example a change in the input to the price function is proportional to the resulting change in the output of the price function (the change in output equals twice the change in input).
Now suppose that, instead of a piece of string, you want to buy a square piece of fabric, priced at 2 pounds per square metre. If the side of the square you want to buy has length $x$ metres, then its area is $x^2$ square metres, so the price of this square is $$p(x)=2x^2.$$
This is a non-linear relationship. When you plot $p(x)$ against $x$ you no longer get a straight line, but a curve.
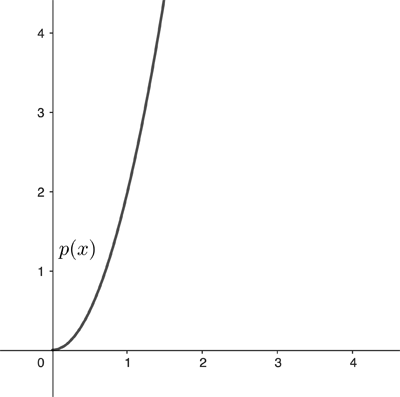
What if you now want to increase the side length of your square by $a$ metres? The square will now have an area of $(x+a)^2$ square metres, so it'll cost $$p(x+a) = 2(x+a)^2= 2(x^2+2ax+a^2) = 2x^2 + 4ax +2a^2.$$
The difference between the price $p(x)$ of the original square and the price $p(x+a)$ of the new square is $$p(x+a)-p(x)= 4ax+2a^2.$$
This is quite a complicated expression involving both the original side length $x$ and the increase $a$. It's no longer possible to quickly work out in your head whether you can afford to buy the larger piece. Specifically, a change to the input to the price function is no longer proportional to the resulting change in the output.
This feature of non-linearity means that it can be difficult making predictions based on non-linear relationships. Indeed non-linear equations can give rise to chaotic systems whose behaviour can be impossible to predict — the weather is an example of a system whose underlying equations are non-linear and exhibit mathematical chaos.
Our equations above were specific examples of linear and non-linear relationships. More generally, the equation of a straight line can be written as $$p(x)=mx+b,$$
where $m$ is the slope of the line and $b$ the point where it cuts the $y$-axis. This gives a linear relationship: if you change the input by some amount $a$, the change in output is always equal to $ma.$
This isn't true for \emph{polynomial} relationships such as $$p(x)=bx^2+cx+d,$$ or exponential ones such as $$p(x)=be^{cx}.$$ These are examples of non-linear relationships.
Even more generally, the concepts of linearity and non-linearity also exist for relationships between more than two variables, or when the variables stand, not for numbers, but other types of mathematical objects, such as functions or vectors. The defining feature of linearity is that changes in output are proportional to changes in input, and of non-linearity that this is not the case. Find out more in the Wikipedia article on non-linear systems.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
