
Brief summary
Imagine something growing over time in such a way that the bigger it is, the faster it grows. Something that may appear to be growing slowly early on (when it is small) grows very fast later on (when it is larger). If the rate at which a quantity grows is proportional to its size , then we have exponential growth. This leads to its most surprising aspect; the explosive nature of exponential growth.
As an example, imagine a standard chessboard with 8 rows of 8 squares, and putting one grain of rice in the first square, two grains in the second square and so on, doubling the amount of rice you put in the next square. Your eighth square – at the end of the first row – will have 256 grains of rice (256=28). But by the end of the second row, your sixteenth square will have over 65 thousand grains of rice.
This is an easy introduction to the concept of exponential growth – you can find a little more mathematical detail here.
What do we mean when we say that something grows exponentially?
As an example of exponential growth, imagine a little biological organism, such as a bacterium. Imagine that a single organism divides into $2$ daughter organisms within the space of an hour. Over the subsequent hour, the two daughter organisms then also divide into $2$ organisms each, leaving us with $2\times 2=4$ organisms. During the third hour, these four organisms also divide into $2$ organisms each, leaving us with $2\times 2\times 2=8$ organisms, and so on.

This is a time-lapse video of an E. coli colony growing on a microscope slide. Credit: Stewart EJ, Madden R, Paul G, Taddei F, CC BY-SA 4.0 DEED.
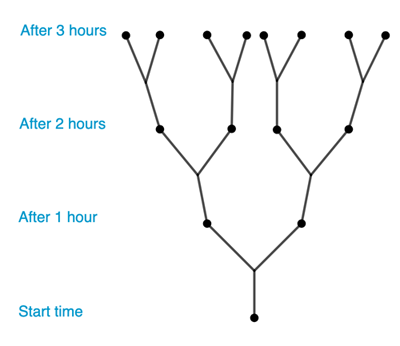
This tree diagram shows how the number of organisms grows over the first three hours.
In general, after the $nth$ hour, there will $2^n$ organisms. The growth in the number of organisms is called \emph{exponential} because we can describe the quantity that changes over time as $2$ raised to the \emph{exponent} $n$. Exponential growth can be very rapid. In our example, within less than 33 hours there will be more organisms than there are people on Earth!
The picture below indicates what happens if we continue our tree diagram above for many generations. We have to make the lines much thinner and rearrange them on the page to make it all fit in. But still, there eventually are so many of them, they form a dense canopy.

This graphic beautifully illustrates exponential growth: the stem splits into two branches, which each split into two branches and so on. Soon there are so many branches, they form a dense canopy.
Exponential growth involves repeated multiplication. We don't come across this kind of growth too often in everyday life. We're much more familiar with repeated addition, that is, calculations of the form $2+2+2+...$ rather than $2 \times 2 \times 2 \times ...$. The growth you get from addition is a lot slower, which is why it's easy to underestimate the speed of exponential growth. (See this video for an illustration of the difference between additive and multiplicative growth.)
An important feature of exponential growth is that it speeds up as time goes on. In our example above, the number of organisms only increases by $1$ during the first hour and by $2$ during the second hour, but you only have to wait for $8$ hours to see an hourly increase of over $100$! This acceleration doesn't happen for additive growth.
Would you like a little more mathematical detail? Then see our slightly longer introduction, which gives you a chance to see the basic mathematical description of exponential growth in action at the end.
This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.
