
Feeling tense about tensors?
Recently we had to learn about tensors for an upcoming article. What are those, you ask? We didn't know at first either. Like some other concepts in maths, they seem confusing at first but actually are just a way of capturing information we are all used to.
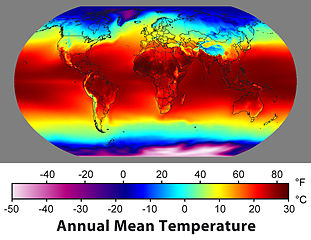
Image created by Robert A. Rohde / Global Warming Art
First of all, let's start with scalars. Scalars are just your ordinary, everyday, real numbers. A scalar field is used to describe something that has a particular value at every point in the space you are considering. For example, a map of temperatures across the UK, or indeed the world, is a scalar field; with a value for the temperature at each point on the map. You can read more about how scalar fields describe dark energy and the Higgs boson.
Then we get to the more dynamic concept of vector fields. A vector field is something that associates a vector (a magnitude and direction) to every point in space. Again, thanks to meteorology we have the familiar example of a wind map as a vector field. Vector fields are incredibly important in maths and physics and, like in our example of a wind map, usually describe how things move. You find out how fluid dynamics uses vector fields to model the movement of tears, wind and waves in Births and deaths in fluid chaos
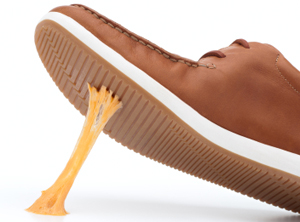
A tensor field
A tensor just extends this definition to one where the value of some property depends on the direction in which you measure it. So where a vector is a magnitude and a particular direction from some point, a tensor gives a magnitude for every direction from that point. A tensor field is something that assigns a tensor to every point in space. Naturally it's harder to picture a tensor field but if you've ever played with a piece of chewing gum you've actually seen one in action. As you pull a piece of gum (or some other rubbery substance) between your fingers, it stretches in tension along one direction but compresses in the other perpendicular directions. So for each point in the gum the stress is a function of direction: in each direction the stress will take a certain value that is a combination of the contributions from these tension and compression stresses.
Tensors are incredibly useful tools, particularly when describing things in higher dimensions. The curvature of multidimensional surfaces (called manifolds) is described with tensors and Einstein used tensors to describe both the curvature and distribution of matter of four-dimensional space-time. You can read more about Einstein and the role of curvature on Plus.
So there you go. Tensors are nothing to get tense about!
Anonymous
I've taken classes in tensors before and needed the "picture" you just gave, because I didn't get what they were about really.
Anonymous
I'm sorry but this isn't correct.
A tensor is a generalisation of scalar, vector, matrix, etc.
A tensor field is a field where each element is a tensor.
So a scalar field is a type of tensor field, a vector field is also a type of tensor field.