Energetic maths: part ii

Usually, thanks to careful planning by the National Grid, and other energy companies, the lights do usually stay on. Sadly, however, this doesn't always happen. On August 14th, 2003 a catastrophe hit the North East coast of America. During a storm, an overgrown tree hit a power cable. The safety mechanisms cut in leading to a local shut down of the power supply to the part of the network closest to the affected cable. Unfortunately, there was a software error in the control room, which meant that the shut down spread and spread. As a result the whole of the North East of America and large parts of Canada were plunged into darkness.

The resulting blackout lasted for about two days, and affected an estimated ten million people in Ontario and 45 million people in eight US states. The event contributed to at least 11 deaths and cost an estimated $6 billion.

Tipping points

So, could this happen again? One of the main reasons for a power failure is a phenomenon called a Voltage Drop and this is directly related to properties of the solutions of a quadratic equation.

Usually a quadratic equation is written as

$ax^2+bx+c=0$

and we want to find the solution $x$ . When we meet the equation at school we are told that it may have one, two or no real solutions. These are given by the famous formula

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$

This formula says that the quadratic equation has two real solutions if $b^2> 4ac$ and no real solutions if $b^2< 4ac$ . To illustrate this we will look at an equation for which $a = 1$ , $b = -2$ . The two solutions are then given by

$x=1\pm \sqrt{1-c}.$

There are two real solutions if $c< 1$ and no real solutions if $c> 1$ . A graph of the two solutions is given below, with the special point $c = 1$ , $x = 1$ (where there is only one solution) highlighted.

A graph showing the two solutions of x²-2x+c=0 for different values of c.

This point is very important as it marks the boundary between when the quadratic equation has two solutions and none. It has various names including a fold point, a saddle-node bifurcation and, most provocatively a tipping point. Tipping points are common, and they are important in many scientific fields,and are also of huge importance in power supply networks.

A nose for trouble

To see this, consider the graph below showing the voltage in a network (shown on the vertical axis) when it has to supply a reactive power Q (shown on the horizontal axis). The curve on the left corresponds to a network with fewer power stations and thus less available power, and the curve on the right to one with more power stations on and thus more available power.

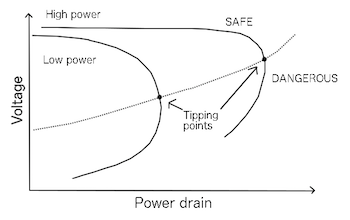
Nose curves – graphs of power versus voltage for smaller and larger networks.

Each of these curves has a very similar shape to that of the solution of the quadratic equation illustrated above, complete with a tipping point. This is of course no coincidence: it turns out that each such curve is given by solving several quadratic equations instead of just one. These curves are given the technical name of nose curves for reasons which should be obvious. (You can find out more about the reactive power and the quadratic equations that result from mathematically describing a network in the next article.)

Each nose curve has, as we might expect, two solutions for a given value of Q before the tipping point. The upper part of the curve represents a stable solution (where slight variations in Q doesn't dramatically change the voltage) in the normal voltage range, which is where we want to operate the power grid. However as the reactive load Q increases a worrying sequence of events occurs. Firstly the supplied voltage starts to drop, and then we get to the tipping point there is no solution at all. What happens at this point is that the grid goes into a very unstable state during which the voltage collapses and all of the lights go out.

It is fair to say that, due to good planning and management by the National Grid Company, the UK has never experienced a widespread voltage collapse. However, it has occurred in both Italy and Sweden as well as in the NE USA, and all because a quadratic equation didn't have a solution. There are other causes of power cuts, for example on 13th March 1989 the particles emitted from a large solar flare so overwhelmed the safety systems of the Quebec power system that a power cut resulted. Quebec also suffered later on from a power cut caused by an ice storm.

Energy matters to all of us, and the challenge of supplying enough energy in a clean and safe way, is one of the greatest challenges faced by humanity. Energy supply networks are already highly sophisticated, and will get more so as the way in which we use and supply electricity is changing rapidly. To deliver a secure supply well into the future will require equally sophisticated mathematics. However, the bottom line is, that to keep the lights on we all need to be able to solve (lots of) quadratic equations.

You can find out more about the quadratic equations that result from mathematically describing a network in the next article.

About this article

Chris Budd.

This article is adapted from one of Chris Budd's Gresham College lectures, part of a series called Mathematics and the making of the modern and future world. The lectures take place in London, are aimed at a general audience and free to attend.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution, Gresham Professor of Geometry, and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin and features in the book 50 Visions of Mathematics ed. Sam Parc.

This is the second of three articles in this series – you can read more in part i and part iii.

This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.