Energetic maths: part iii
Producing electricity securely, safely, reliably and cheaply, has many challenges. Electricity is difficult to store in large quantities, so it usually has to be used as soon as it is generated. We also have a very low tolerance to any interruption in the electricity supply. Other challenges arise from the extreme interconnectedness of the electricity network, which means that a problem in part of the network quickly becomes a problem for the whole network. It turns out that the answer to many of these issues is Maths.
Your electricity bill will usually be given in kilo Watt hours (KWh) – the amount of energy required to supply a kilo Watt for one hour (the rough average power consumption of a typical household). The annual consumption of electricity in the UK is about 360 TWh (a TWh is one Tera Watt hour, which is one billion kilo Watt hours), and is predicted to rise to 730 TWh in 2050. The peak demand is around 70 GW (at any one instant), depending upon the time of day and the day of the week.
Complex networks
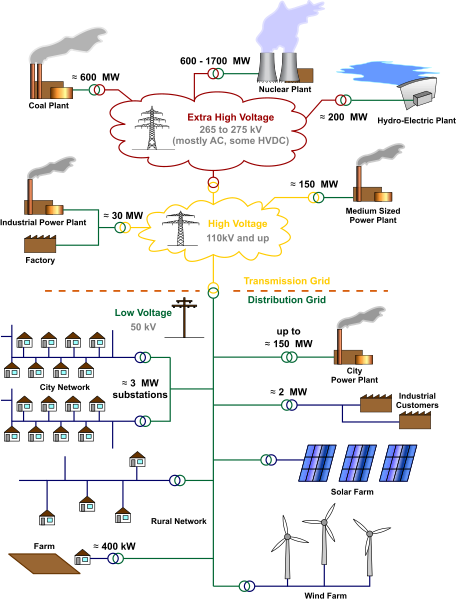
This electrical power is supplied over a network starting, usually, with power being generated at a power station. This is then transmitted over a high voltage network, before being reduced in voltage and distributed to commercial, industrial and residential consumers.
Each junction in a power network is called a bus; buses can be power stations, factories, transformers, switches, points where the network changes, and households. In principle there can be one bus for every household, so there are up to 30 million buses in the UK. This immediately gives you some idea of the scale and the complexity of the electricity supply network.
Between the buses there are connections, such as the high voltage cables that we see proudly marching across the countryside. The cables carry current between the buses, which is kept low by having a high voltage. This is because voltage is inversely proportional to the current for constant power, as $S=VI$ where $S$ is power, $V$ is the voltage, $I$ is the current. Low current leads to much smaller power losses, which is why high voltages are used.
At each bus the network needs to supply a certain amount of power. How much depends upon the usage at that bus: for example the requirements for a factory would be very different for that for a household.
To describe the electricity network mathematically, number each of the $N$ buses in the network with an index $j=1,2,3,\ldots N$. Then we can write $V_j$ for the voltage at the $j$th bus. This voltage is written as complex number, as we saw in a previous article, in order to give two pieces of information: the amplitude and the phase of the waveform of the voltage (the frequencies of the voltage and current waveforms are always a constant 50 Hertz).
Each bus will in turn be connected to many other buses in the network. Typically a current $I_{j,k}$ (again a complex value) will flow between the buses labled $j$ and $k$ in the network. The power $S$ of this current flow is given by \begin{equation} S_{j,k}=Vj I_{j,k}^* \end{equation} where $I_{j,k}^*$ is the complex conjugate of the current. (For a complex number $a+ib$, the complex conjugate is $a-ib$). The total power at the $j$th bus is then the sum of the power for all the connections from this bus to other buses in the network: \setcounter{equation}{1} \begin{equation} S_j=S_{j,1}+S_{j,2}+\ldots +S_{j,N} \end{equation} This power is in turn a complex number and we write $S_j= P_j+i Q_j$. Here $P_j$, the real part of this complex number, is called the real power, which is the power which does work, such as heating your home. In contrast $Q_j$, the imaginary part of the complex number, is called the reactive power. The real power averaged over a complete cycle of the AC waveform results in net transfer of energy in one direction. The reactive power is that portion of power due to stored energy, which returns to the source in each cycle.
Easy as ax2+bx+c
Electrical engineers take all of the power into account when designing and operating power systems, because although the current associated with reactive power does no work at the load, it still must be supplied by the power source. Failure to provide for the supply of sufficient reactive power in electrical grids can lead to lowered voltage levels and under certain operating conditions to the complete collapse of the network and a power blackout, as we saw in the last article.
If the voltage difference between two buses is $V_k - V_j$ then the current $I_{j,k}$ flowing between them is given by Ohm's law. In particular there is (another) complex quantity called the conductance, $\sigma_{j,k}$, which allows us to calculate the current \setcounter{equation}{2} \begin{equation} I_{j,k}= \sigma_{j,k} (V_k-V_j). \end{equation} (In high voltage cables the conductance is usually close to being a purely imaginary number. This is because these cables are designed to have a very low resistance, but usually have some inductance.)
We can now combine the three equations (1),(2) and (3) to find that the total power supplied to the $j$th bus is given by the expression \setcounter{equation}{3} \begin{equation} S_j= V_j \sigma_{j,1}^* (V_1^*-V_j^*) + V_j \sigma_{j,2}^* (V_2^*-V_j^*) +\ldots +V_j \sigma_{j,N}^* (V_N^*-V_j^*). \end{equation} Now, when designing and controlling a power supply network, we know the values of the real and reactive power that needs to be supplied to each bus: $P_j$ and $Q_j$ at the $j$th bus. Therefore, the voltages at each bus must satisfy the equation: \setcounter{equation}{4} \begin{equation} V_j \sigma_{j,1}^* (V_1^*-V_j^*) + V_j \sigma_{j,2}^* (V_2^*-V_j^*) +\ldots +V_j \sigma_{j,N}^* (V_N^*-V_j^*) = P_j+ iQ_j \end{equation}
The important equation (equation 5) allows us to work out the voltages at each bus which are needed to supply the desired amount of real and reactive power. Take a look at it. It is nothing other than a large collection of a type of quadratic equations that describe the voltages.
We can understand the complex behaviour of the grid by looking at the complex solutions of quadratic equations. It is worth noting that an attempt was made a few years ago to stop the teaching of quadratic equations at school on the grounds that they were totally useless and would frighten the students! (More details of this debate are given here.) However, we need to solve quadratic equations if we want to keep the lights on!
About this article

Chris Budd.
This article is adapted from one of Chris Budd's Gresham College lectures, part of a series called Mathematics and the making of the modern and future world. The lectures take place in London, are aimed at a general audience and free to attend.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution, Gresham Professor of Geometry, and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin and features in the book 50 Visions of Mathematics ed. Sam Parc.
This is the last of three articles in this series – you can read more in part i and part ii.
This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.