Being squeamish I've never really liked to think about how exactly wounds heal. But I now have the courage to ponder this miracle of biology, because I can now think about it using maths. Researchers from the University of Pittsburgh have just published a new mathematical model of how some wounds heal.

Rather than looking at external wounds to our skin, their model concerns wounds to the much simpler internal linings of our bodies. These epithelial layers, such as the lining of our digestive tract, are just one cell thick. Holes in this epithelial layer are healed by the surrounding cells moving towards the wound, stretching to close the breach. The cells move across the underlying tissue by extending and elongating their "front" (in terms of direction of travel), moving their nucleus forward, and releasing their back edge from tissue underneath.

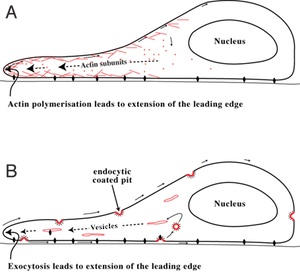
Two models for how a cell may move, both showing the front edge of the cell extending, allowing the nucleus to move forward before releasing the back edge. For more information on cell migration see wikipedia. Image by Bulbeck

The layer of cells around a wound move in a coordinated way, with the cells in the wound edge moving in conjunction with the cells further away from the injury. "There are several hypotheses about how this coordination is accomplished," says Professor David Swigon, one of the authors of the paper. "But we believe that the underlying mechanisms are mechanical in nature, resulting from forces exerted by the cells and the [underlying tissue]."

The cells in the epithelial layer are held together by stretchy proteins. When the cells are close together they push against each other and as they move apart they tug at their neighbours. The cells are also held in place by the underlying tissue, which acts as a traction against the skin cells moving.

The researchers used mathematics to model the movement of the cells by describing the density of cells and the tension and stresses across the layer. In their model epithelial cells move from an area of higher density to one of lower density, with any movement of cells rippling back causing their neighbours to move in response. When there is a hole in the epithelial lining, the push from the cells behind the wound edge causes the edge to move towards the injury. And as the cells near the wound edge spread out and become less dense, they in effect pull more cells with them. Finally the wound closes and the densities of cells, and therefore the tensions within the layer, are back in balance.

When compared with lab observations of wound healing this mathematical model accurately predicted the speed of wound closure, the changing shape of the wound and the density of cells within the skin layer. It agreed with experimental observations that initially the wound edge moves quickly, and then slows down until the wound is fully healed.

One advantage of this approach is that the model resolves into a well known mathematical problem. "The physical laws governing the mechanics of the layer then yield a partial differential equation problem with moving boundary that is known as the Stefan probelm in other contexts," say the researchers. This enabled them to use existing techniques for tackling this class of problem to predict the healing of wounds with their model.

Previous models of cell migration have described the layer of cells as a collection of randomly moving, non-interacting cells. "Our model is based on physical principles of the balance of forces within the moving layer, and accounts for the cohesion of the cell layer," says Swigon. In addition to improving our understanding of cell migration, Swigon and his colleagues believe it can also benefit the medical community.

One such benefit might be more accurate predictions of wound healing time. "We are currently working on a method for determining the time of closure for wounds of various shapes and sizes," says Swigon. The researchers are also conducting experiments in which the migration of cells is inhibited by bacterial toxins, trying to analyse which interactions during cell migration are most affected by these chemicals. "The ability of the model to predict wound-closure times for complex initial wound geometries, including those that lead to a change in wound topology, could be of great benefit in medical applications."

And the next time someone dear to me hurts themselves, I'll be much braver — it's just a complex maths problem that the body is trying to solve. Perhaps even more reassuring than a sticky plaster!