Clocking the schedule

In 2007 the Norwegian Premier League was won by Brann Bergen. Fans were ecstatic and everyone agreed that victory was down to the Brazilian player Alanzinho. Only Alanzinho wasn't playing for Brann Bergen — he played for the rival team Stabaek. So what happened?

Behind Brann Bergen's victory was a phenomenon football fans will be familiar with, though it's not often talked about explicitly. Stabaek, with the help of the talented Alanzinho, had trashed team after team during the tournament. In 22 of the 26 rounds Brann Bergen were lucky to play the trashed team right after Stabeack had. "This was seen as an advantage for Brann Bergen: they could systematically play against a weakened team," says Dries Goossens, Professor of Operations Research at the University of Gent. "Weakened because the [losing team's] game against the previous opponent had resulted in red cards and suspensions, and they had been demoralised by the first defeat. So the schedule made it easy for Brann Bergen to become the champion."

Generally we say that team A gives a carry-over effect to team B whenever team A plays a third team, team X, in one round, and team B then plays team X in the next round. The carry-over effect can result in an advantage for team B, as in the example above, but it can also result in a disadvantage. "You could get a boost as an intermediate team [team X] because you played against a weak team and come to the next team with full confidence," explains Goossens. In this case, team X would benefit and team B suffer. But no matter who profits, it's clear that a tournament should be scheduled to avoid long strings of carry-overs between the same two teams, like the one that occurred in the Norwegian league.

Goossens has been responsible for scheduling the Belgian Pro League, together with Frits Spieksma, since 2006. When they started this job, Goossens and Spieksma were aware of the carry-over effect and decided to see how various other football leagues dealt with it. Given the effort, care, and money that usually goes into anything related to football, the answer is surprising: many European leagues dealt with it the worst way possible.

Spin the clock

Many major leagues, including the German Bundesliga, La Liga in Spain, and the Primeira Liga in Portugal, used a neat and very old geometric method to do their scheduling. This clock method was invented by English mathematician Thomas Penyngton Kirkman in 1850 to solve the so-called schoolgirl problem, which has a similar sudoku-like quality as the problem of scheduling a tournament.

Here is how it works. If your tournament contains n teams (where n is an even number) start by writing the first n-1 letters of the alphabet in a circle. Then write the last letter in the centre of the circle, and connect the letters by lines in the pattern as shown below for the example of n=8 (an analogous pattern works for any even number n):

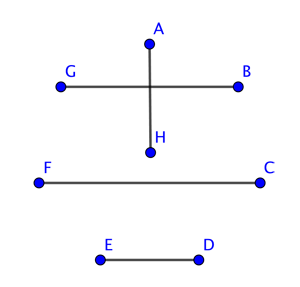
This gives you the pairings of the first round in the tournament. Now keep the letters where they are, but turn the line arrangement clockwise by one letter, to get the following arrangement:

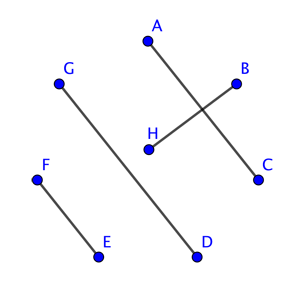
This gives the pairings for the second round. Keep turning the lines by one click until you're done. At the last step your line pattern looks like this:

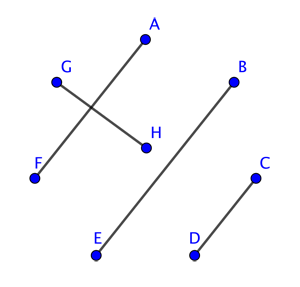
The result is a full schedule over n-1 rounds in which every team plays every other team exactly once and in which there are no clashes.

Round 1	Round 2	Round 3	Round 4	Round 5	Round 6	Round 7
A-H	A-C	A-E	A-G	A-B	A-D	A-F
B-G	B-H	B-D	B-F	C-G	B-C	B-E
C-F	D-G	C-H	C-E	D-F	E-G	C-D
D-E	E-F	F-G	D-H	E-H	F-H	G-H

Once you have this skeleton of a schedule — called a roster — you still need to impose a home-and-away pattern, create the schedule for the return legs of the matches and, importantly, assign the actual teams to the letters in a way that satisfies other constraints you might have, such as teams sharing a stadium not being able to have home matches on the same day. A home-and-away pattern can also be determined using the clock method (see here), but we'll ignore these extra tasks and instead see how the schedule we have created fares with respect to carry-over effects.

As indicated by the colours in the table above, team F gives team A a carry-over effect five times. Given that in this example there are only seven rounds in total, that doesn't bode well. To see how the carry-over effect plays out over the whole tournament, you can create a carry-over table. The entry corresponding to row X and column Y is the total number of times team X gives a carry-over effect to team Y. The carry-over table for our example shows up a very pretty pattern, but it's not a pattern you'd want. There are seven pairs of teams for which one gives the other a total of five carry-over effects.

	Team A	Team B	Team C	Team D	Team E	Team F	Team G	Team H
Team A	0	1	5	0	0	0	0	1
Team B	0	0	1	5	0	0	0	1
Team C	0	0	0	1	5	0	0	1
Team D	0	0	0	0	1	5	0	1
Team E	0	0	0	0	0	1	5	1
Team F	5	0	0	0	0	0	1	1
Team G	1	5	0	0	0	0	0	1
Team H	1	0	1	1	1	1	1	0

(A small technical note: in computing this table we have assumed that the schedule is cyclical, so that a team playing in the last round can give a carry-over effect to a team playing in the first round. This makes sense if the schedule is mirrored for the return legs of the matches, that is, if it is played a second time with the home-and-away pattern reversed. However, even if we hadn't made this assumption, the spirit of the results wouldn't change.)

There seems to be something systematic about the way the carry-over effect weaves through this schedule, so Goossens and Spieksma, together with Erik Lambrechts and Annette Ficker, decided to take a closer look at the theory. What they found, and proved mathematically, is that when it comes to the carry-over effect, you can't do any worse than using the clock method.

That's quite a shocking result. "It's the most common schedule used in football, and also in other sports, but it's the worst thing you can do for that basic fairness issue," says Goossens. In the academic literature the carry-over effect was first mentioned in the 1980s, but for some reason it just hasn't been given much attention. "People are either not aware of it, or if they are aware of it, they don't know the name for it," says Goossens.

Doing their worst

In what way is the clock method the worst you can do? An accepted way of measuring the strength of the carry-over effect over a whole schedule is to add up the squares of the numbers in the carry-over table. (The reason we sum the squares of the numbers in the table is that summing just the numbers themselves would give the same result for each schedule.) In our example above, this carry-over value is 196. Goossens and his colleagues proved that a schedule produced using the clock method always gives the largest carry-over value possible. And conversely, any table that has a maximal carry-over value can be generated with the clock method, for example by changing how the letters are arranged in the circle.

To give you an example of just how bad the clock method can be, consider a tournament with n=20 teams. The best-known schedule (in terms of avoiding carry-over effects) delivers a carry-over value of 380. The clock method delivers a carry-over value of 5548. For n=24 the values are 644 and 10212. Those are huge differences!

Striving for balance

The clock method definitely isn't the way to go. Ideally we'd like a schedule in which the carry-over effects that a team dishes out over the whole schedule are evenly spread among the other teams, that is, a schedule in which every team gives every other team (apart from itself) exactly one carry-over effect. Such a table is balanced. (See here for an example of such a schedule for a tournament with eight teams.) The carry-over value of a balanced table is always $n(n-1)$, where $n$ is the number of teams. By contrast, the carry-over value of a schedule created using the clock method, as Goossens and his colleagues proved, is always $((n-3{)}^2+3)(n-1)$.

Finding balanced schedules, however, is easier said than done. Looking at tournaments containing up to 24 teams, we only know balanced schedules for n=4, n=8, n=16, n=20 and n=22 teams. For the other value of n we either know that a balanced table doesn't exist, or haven't got a clue as to whether it exists or what it is. The table below tells you which option applies for each n. More generally, it's known that a balanced table exists for every n that is a power of 2, but as the examples of n=20 and n=22 show, some values of n that are not powers of 2 also admit balanced tables. It's amazing that a task like football scheduling can uncover unsolved mathematical problems!

n	Best known carry-over value	Balanced?
4	12	Yes
6	60	Doesn't exist
8	56	Yes
10	108	Doesn't exist
12	160
14	234
16	240	Yes
18	340
20	380	Yes
22	462	Yes
24	644	Doesn't exist

There is some good news, however. "As soon as you start deviating from the clock method, it gets better very quickly," says Goossens. "Just a few changes already produce a much more balanced schedule."

To produce alternative schedules Goossens recommends using mathematical methods that have been specifically designed to solve problems that are subject to a number of constraints, such as so-called integer programming. Once such a method has given you a roster, you can combine it with the home-and-away pattern from the clock method schedule (see here). This can drastically reduce the carry-over value of a schedule and still retain some of the advantages of the schedule that was produced by the clock method.

After the 2007 debacle Norway introduced an explicit rule to make sure that schedules are reasonably balanced. In Belgium there isn't an explicit rule, but as long as Goossens is in charge of scheduling, we can be pretty sure that carry-over effects are taken care of. Whether awareness of the carry-over effect will grow around the world and across different sports remains to be seen. But one thing's for sure: having an expert in maths doing your scheduling can only be a good thing.

---

About this article

Dries Goossens is Professor of Operations Research at the University of Gent. He talked to us at a Fairness in Sports and Games workshop which took place at King's College, London, in June 2018. Goossens is a board member of the EURO working group OR in Sports, which also sponsored the Fairness in Sports and Games workshop.

Marianne Freiberger is Editor of Plus.