
Have you heard? The maths of rumour spreading
"A rumour without a leg to stand on will get around some other way." - John Tudor

How fast and wide does gossip spread?
Rumours are everywhere. They circulate around schools, lie at the heart of political campaigns and — at their worst — can leave people fatally misinformed. In the age of social media it has become even easier for gossip to spread, often in the form of what's trending. Amongst other things, this has led to countless death hoaxes that in their time have concerned almost every known celebrity at least once. More sinister perhaps were the famously ill-informed reports on Andrew Wakefield's flawed study of the MMR vaccine, which led to a huge increase in unvaccinated children.
Despite this, the familiar wide-spreading influence of the rumour mill can also be harnessed for potential good. Studying the spread of rumours allows us to understand how misinformation spreads, and can in turn help us to counter the effects. Alternatively, inside knowledge of how rumours work can be used to disseminate information quickly in an emergency, or create effective viral and political marketing campaigns.
Can you unring a bell?
If you've ever been the victim of malicious gossip, you'll know how quickly it seems to spread. When news appears to travel around an entire school or workplace in almost no time at all, it is hard to believe that anybody could be left in the dark — and yet we all have anecdotal evidence that suggests otherwise.
One particularly good tool for explaining the counterintuitive, and seeing if it really is the case, is the mathematical model, and in this instance there is already a group of models to hand. SIR models (Susceptible, Infected, Recovered) are used to study the spread of epidemics and have been adopted and adapted to describe the spread of a rumour; so if someone tells you that a piece of news has spread "like an epidemic" they're closer to the truth than they might think.
Imagine you are in the midst of a class election. To put the electorate off voting for Candidate B, Candidate A has been telling people that their opponent is more invested in his status as teacher's pet than promoting the common good. This is a particularly tactical campaign for a schoolchild, so no-one is cynical about what is being said. The pupils now fall into three categories: those who know and will pass on the rumour (Spreaders); those who know and won't pass on the rumour (Stiflers), and those who don't yet know the rumour (Ignorants). At this point you could argue that a variety of different behaviours will surface in each group, but for simplicity's sake we will limit them to a few basic rules:
- At the start there are only Ignorants and Spreaders.
- All Ignorants will become Spreaders if and when they first hear the rumour
- All Spreaders will tell the rumour to everyone they meet until they come across either another Spreader, or a Stifler — at this point they will decide that the rumour is known and become a Stifler.
- The rumour ends when there are only Ignorants and Stiflers remaining.
By using the very simple definitions and rules shown above, translated into numbers, symbols and equations, and also using equations to describe the rate at which people pass from one category to another, it is possible to estimate the proportion of the pupils who will eventually hear the gossip. Perhaps surprisingly, this will only be about 80% of them (it goes up to around 85% if half the class know the rumour to begin with). You can read the details in the paper On the size of a rumour by Ray Watson, or find out about the SIR model in the context of epidemics in the Plus article The mathematics of diseases.
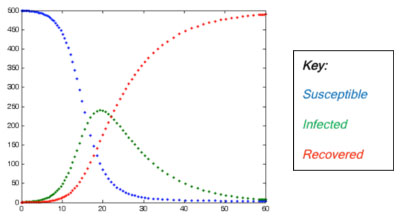
A SIR model at work. The vertical axis shows the number of people in each category as time goes by.
Could this ever be good news for the victim of this particular smear campaign? If it's a believable lie, then probably not, even with approximately 1/5 of voters remaining unbiased. Not-so-counterintuitively, one thing the results show clearly is that, to do as much damage as possible, Candidate A should tell as many classmates as possible. So can you unring a bell? Maybe sometimes you just have to wait for gossip to become old news, but while you're waiting, take comfort in the fact that the bell probably stopped ringing before everybody got to hear.
Around the world in 45.4 days
The SIR model gives some idea of how a rumour might spread, but a more pertinent question for anyone who wants to disseminate information quickly is how fast? If we know that, we can make improvements — to the model and real life — to get the news out even faster.
To do so, it is easier to (temporarily) forget about Stiflers and imagine that eventually everyone will know the rumour. An ideal population would be something like that of a small village, where everyone knows each other and gossip spreads like wildfire.
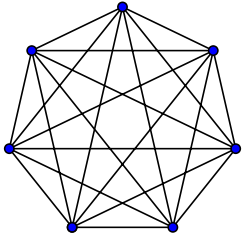
A complete graph with seven nodes.
Mathematically this can be modelled by something called a complete graph. A graph is a collection of points (nodes) joined together by a collection of lines (edges). In a complete graph every node is connected to every other node.
Each point in the graph represents a villager, and the lines depict connections between pairs of villagers. Quite suitably, a collection of points within any network which are all connected (as in a complete graph) is called a clique.
To begin with suppose that only one person is aware of the rumour. Knowing this, you can ask what would happen if any pair of villagers happens to meet in the street, and one has the chance to pass the news on: if they know the rumour, they spread it to the other villager; if not, they don't.
In order to work out how long it takes for a rumour to spread, you need to estimate the probability of any potential exchange between two villagers occurring. As you may have noticed, mathematicians like to keep things (relatively) simple, and in this case that means considering the connections between the villagers, as opposed to considering each individual separately. In other words, it allows you to look at the chance that one particular villager will bump into another and pass on the gossip, as one combined probability which considers both villagers.
Using the probabilities chosen for each interaction — which we take to be all the same — a mathematical model designed by A.J. Ganesh predicts that on average, for $n$ people, everyone will have heard the news after $2\log{(n)}$ units of time. What the time units are depends on how quickly the rumour is passed from person to person; it would go faster between rooms on a hotel corridor, for example, than between houses on a street. (The $2\log{(n)}$ is the expected value, see Ganesh's paper for details.)

Networks can be complex, but they usually contain cliques in which everyone knows everyone else.
So if you wanted to know how long it would take for everyone in the world to find out about your latest crush, and you only managed to keep the secret for a day, then you should have on average $2\log{(7,260,711,000)}$ or 45.4 days to plan your next move (7,260,711,000 was the estimated world population in 2014 according to the World Bank). That is assuming that you are equally close to each of the 7,260,711,000 other people on this planet, and they're all pretty tight too. More reasonably, if you wanted to know how quickly the news would spread amongst your peer group — or clique — you might find the answer given by the formula to be a little closer to home.
A common (and often valid) criticism of many mathematical models is that they are too simplified to describe real life well. Though that could be argued for the examples given here, it is not always the case, or indeed, always an issue. While these particular models were chosen for their simplicity, they still give some idea of the way that rumours spread. It is also true that many more complicated models are used every day to inform everything from advertising campaigns to so-called gossip algorithms which let lots of computers share information quickly.
As someone who'd never really considered it before, I was certainly surprised to find that when you search for "rumour spreading" on the internet, along with advice sites, you are hit by a wave of mathematical studies. Recently, such studies have even started to consider detecting the source of a rumour. You didn't hear it from me, but with insight like that, even internet anarchists may have to start thinking carefully about what they say online.
Further reading
You might also want to read the article What do you think? which explores mathematical models of opinion formation.
About the author

Martha Bozic is 18 years old and about to begin studying mathematics at Durham University. She is especially interested in finding ways to share her enthusiasm about maths with others.
Comments
William Muñoz
This is great information to spread (in a sarcastic way) as a rumor! Excellent write-up knowledge is power!