How did you vote in the brexit referendum? Whichever way it was, your decision was probably influenced, not only by information from the media, but also by the opinions of the people around you. No person is an island: the opinions that prevail in a society emerge from lots and lots of interactions between individual people.

Opinions emerge from interactions between many people.

At the European Congress of Mathematics, which took place in Berlin last week, Bertram Düring presented some work which explores this fact. "We're interested in modelling and analysing emergent behaviour in systems that consist of many interacting individuals," he explains. "For example, the formation of opinions in a society, or the formation of prices in a financial market. We want to understand how certain patterns emerge in such a system and how this whole process works."

Societies (or financial markets) contain far too many people (market participants) to track their behaviour individually, so at first sight it's hard to imagine how to attack the problem Düring talks about. But there's a precedent from an entirely different area. Gases, such as the air in your room, contain far too many molecules for us to track their individual behaviour, yet we still understand their bulk behaviour. For example, there is a famous equation named after Ludwig Boltzmann which (if you manage to solve it) tells you how many molecules you can expect to find in a given region of space, and travelling with a particular velocity, at a given moment in time. To derive the equation, you start with some basic assumptions of how individual molecules move and what happens when two of them collide.

"People are not particles," says Düring. "So we don't use statistical physics and apply it to people. What we do is to try and model the interactions between individuals, translated into a mathematical language. We don't want to follow exactly what every individual thinks, but we want to look at society at an aggregate level. And this where the mathematical tools that were developed [in statistical physics] come into play. We try to derive an equation which describes the formation of opinions in the whole of society."

People and particles

During explaining Toscani's model at the ECM in Berlin.

In 2006 the Italian mathematician Giuseppe Toscani came up with such an aggregate model of opinion formation. The idea is that when two people meet and talk about a particular issue or product, they usually come away with altered opinions. That's a bit like particles in a gas, which, after they collide, come away with altered velocities: they change their speed and their direction of travel.

In analogy to Boltzmann's ideas, Toscani derived an equation that tells you the distribution of opinion in a society: how many people hold opinions with a given value of the opinion variable at a given moment in time. That's the kind of thing you want to know if you are trying to understand how opinions evolve.

Underlying Toscani's model are some basic assumptions about what happens when two people meet and exchange opinions. But how do you describe this interaction mathematically? It's interesting to have a quick look at Toscani's approach, even if you don't understand the equations (see box) in detail. Toscani represented each individual's opinion about a particular issue or product (say brexit, or a new type of mobile phone) by a number on a continuous scale from -1 to +1. For example, -1 might mean "I absolutely want out of the EU", 1 might mean "I definitely want to stay in it", and 0 represents the undecided.

"Sociology tells us that after [two people interact] there is often some sort of consensus: our opinions tend to get closer to each other," explains Düring. Toscani's expression contains a component that represents this compromise process. But since personal contact isn't the only thing that makes our opinions, the expression also contains a component that represents an individual's self-thinking: the way they might change their ideas, for example in response to information from the media. The two components aren't the same for all individuals, rather they reflect the fact that people with extreme opinions tend to be pig-headed: how open an individual is to changing their mind depends on the strength of opinion they already have. Those expressions (see the box) form the basis of Toscani's model and lead to a Boltzmann-like equation for the opinion distribution.

Trends and territories

The maths behind this gets quite complex, but the assumptions about human behaviour aren't: the model is still simplistic in that respect. An aspect it ignores, for example, is one of my own personal frustrations, namely that people tend to pay less attention to my opinions than they do to those of certain other people I know. But Düring and his colleague Marie-Therese Wolfram have extended Toscani's model to take account of just that phenomenon.

"We can also have additional variables which model the details of the consensus process, for example how persuasive individuals are," says Düring. "This could be seen as a characteristic of opinion leaders: this is a group of people within society who have a very strong influence on the common people in the dissemination of opinion."

Similarly, it's possible to add a variable representing where in a country an individual lives — looking at the results of the recent referendum, or even the last general election, that's clearly an important factor too.

Once you have developed a mathematical model, your next task is to see what it tells you for particular starting assumptions. You can choose the parameters in the model (in Toscani's model that would be things like the compromise parameter $\gamma$) in a way you think reflects particular real-life situations, and then see what the model predicts. Düring and Wolfram have found some interesting results, in particular when it comes to the relationship between opinion and geographical location. A particularly striking phenomenon happened in presidential elections in the US over the last few decades. Democrat and Republican voters clustered geographically, and the clustering intensified over the years, leading to a deep political division between the various counties. In 2008 the journalist Bill Bishop suggested that the clustering reflects a trend for US citizens choosing to live near people who are politically like-minded. A worrying idea, since such a trend would lead to even more confrontation in US politics. The trend is exemplified by the state of Arizona:

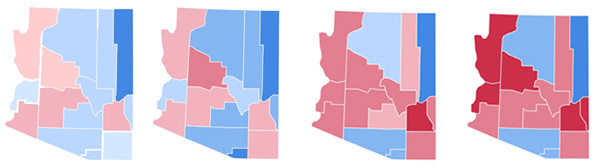
Results of the presidential elections in Arizona in, left to right in 1992, 1996, 2000 and 2004. Republicans are red and Democrats blue. The colour intensity reflects the election outcome in per cent, i.e. dark blue corresponds to Democrats 60–70%, medium blue to Democrats 50–60% and light blue to Democrats 40–50%. Similar colour codes are used for the Republicans. Image adapted from Wikimedia Commons, used under Creative Commons Attribution-Share Alike 3.0.

Düring and Wolfram ran their model including the geographical variable, assuming that people tend to be influenced by people who are geographically close to them, and that they feel drawn to counties that are controlled by the political party they support. They started their model with the proportion of Democrat and Republican supporters like that of 1992, and then let it evolve in time. The result is a political map quite similar to the real one. The exception is the county of Navajo, but that should come as no surprise. Much of its area is covered by the Navajo, Hopi and Fort Apache Indian reservations, to which people wouldn't move as freely as they would to other locations.

Distribution of Democrats (left) and Republicans (right).

Models like Düring and Wolfram's could be used to test suggestions like Bishop's more extensively, but they also find wider applications. They could be used in conjunction with polling to predict likely outcomes of elections and referenda, and also in the worlds of marketing and finance. "There's a fast-growing literature in this area of emergent phenomena," says Düring. "We already have a better understanding of how consensus works in a society. We can't say that we understand everything, and probably we will never completely understand human behaviour. But we're not trying to understand how individuals think, we are just trying to understand how opinion disseminates through society."

One important task that lies ahead is to learn from real-life data what the various parameters in such models should be. This will involve, not only sophisticated mathematical tools, but also insights from the social sciences. And the relationship between maths and the social sciences isn't one-way. "In this century where we are able to store and acquire a lot of data, I think there's a stronger drive to make science even more quantitative. Results in the social sciences tend to be qualitative — when we want to use these results in our models we have to translate them into a more mathematical and quantitative language. I think the process could also go the other way, with the social sciences taking up a more quantitative approach. This is a fairly new field so I expect there to be some new and unexpected results in the future."

About this article

Düring and Wolfram have published their work in the paper Opinion dynamics: inhomogeneous Boltzmann-type equations modelling opinion leadership and political segregation.

Marianne Freiberger is Editor of Plus. She interviewed Bertram Düring at the European Congress of Mathematics in Berlin in July 2016.