
Loo-Q: Clearing aisles and relieving passengers
Suppose you're on a plane with a very narrow aisle and only one toilet. If you need the loo, you could just get up and stand in a physical queue. But that means you can't keep watching your movie. And, more importantly, you'll also block the aisle and the drinks trolley won't be able to get through. To avert this crisis in the skies, we propose the LamportPlus Loo-Q system!
Clear aisles, fair queues, no negotiations required
No one is thinking clearly on a long flight, and no one wants to get into complex negotiations for how queues should work, particularly when people are busting for the toilet. The solution we need is something that can do the following:
- No queue forms in the aisle – the drinks trolley can always get through;
- Fair is fair – requests for the toilet are granted in the order in which they are made;
- Everyone who has requested the loo will eventually get to go (well, at least up until the point the plane begins its descent for landing);
- Finally, perhaps the most vital thing is that there is no need to talk to anyone. And you get to stay in your seat watching your movie for as long as possible.
To solve this problem for us the passengers, and to do it as easily and cheaply as possible for the airlines, our Loo-Q program just needs to be added to the in-seat entertainment system. Then each seat will run its own queue and no central computer is necessary to coordinate things. Loo-Q is a distributed system: the entertainment system in each seat runs a separate process, communicating with the other processes (ie, seats) via messages. (You can read more about distributed systems in Distributed systems and ambiguous histories.)
For simplicity we need to make a couple of assumptions:
- For any two seats $S_i$ and $S_j$, the messages from $S_i$ to $S_j$ are received in the order they are sent, and every message sent will eventually be received. (You could make sure of this by introducing message numbers and acknowledgement protocols – but we're keeping it simple here by making this assumption).
- Every seat can message every other seat.
The algorithm
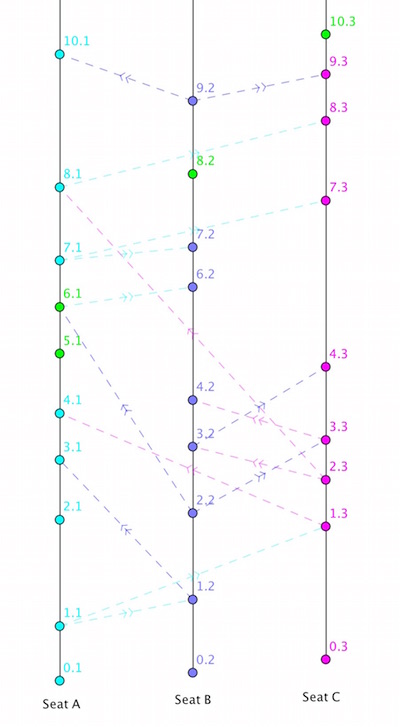
The spacetime diagram for an example of the Loo-Q system in action! You can see the example in full here.
The Loo-Q algorithm is based on the example in Leslie Lamport's paper Time, clocks, and the ordering of events in a distributed system, that is one of the most cited papers in computer science. The Loo-Q system works by every seat maintaining its own local queue, $Q_i$ for seat $S_i$. The local queues work according to the rules listed below. The actions of each rule form a single simultaneous event, and we use Leslie Lamport's logical clocks to make sure we don't violate causality.
Rule 1: If you need the loo you press your Loo-Q button. Your seat, $S_i$, increases the time on its local clock $C_i$ by 1, and sends the timestamped message "$C_i: S_i\mbox{ needs loo}$" to all the other seats. Your seat also adds this message to its own local queue: $Q_i$, which is ordered by the timestamps on the messages, the earliest coming first in the queue.
Rule 2: If your seat, $S_i$, receives a message "$C_j: S_j\mbox{ needs loo}$" from seat $S_j$, it must obey Lamport's rules for logical clocks. Your seat must increase the time on its local clock $C_i$ by at least 1, so that it is greater than the timestamp on the message: $C_i>C_j$. Your seat adds the message from the seat $S_j$ to your seat's own local queue, $Q_i$ (respecting the order of the timestamps). And it sends a timestamped message back to $S_j$, "$C_i:\mbox{ request received}$".
Rule 3: Your Loo-Q button, for seat $S_i$, will go green when it's your turn to go to the loo. This happens if:
- There's a "$t: S_i\mbox{ needs loo}$" request at the front of your local queue $Q_i$ (so no other timestamped requests come before it); and
- Your seat, $S_i$, has received a message from every other seat timestamped later than $t$. (So either a receipt message – Rule 2, a request message – Rule 1, or a release message – Rule 4).
Rule 4: When you've finished with the loo and returned to your seat, your seat increases its local clock $C_i$ by 1 and turns your Loo-Q button off. Your seat removes your request "$t: S_i\mbox{ needs loo}$" from your local queue $Q_i$, and sends a "$C_i: S_i\mbox{ has finished}$" message to all other seats.
Rule 5: If your seat, $S_i$, receives a "$C_j: S_j\mbox{ has finished}$" message, it increases its local clock, $C_i$, by at least one, so that $C_i>C_j$. It removes any "$t: S_j\mbox{ needs loo}$" message from its local queue, $Q_i$. (So it's no use trying to rig the system by queueing up future visits to the loo by repeatedly pressing your Loo-Q button, they're all deleted when you've finished your first visit.)
Rule 6: If your seat, $S_i$, receives a receipt message "$C_j: S_j\mbox{ request received}$", it again increases its local clock, $C_i$, by at least one, so that $C_i>C_j$.
You can see a worked example, showing the Loo-Q system in action for three of the seats on a plane, here.
Clear aisles and relieved passengers
You might ask: Why go through all this palaver? It will be well worth it if it meets the specifications we set for our Loo-Q system:
- No queue forms in the aisle – the drinks trolley can always get through;
- No queue jumping – requests for the toilet are granted in the order in which they are made;
- Everyone who has requested the loo will eventually get to go (well, at least up until the point the plane begins its descent for landing);
- No need to talk to anyone – you get to stay in your seat watching your movie for as long as possible.
No queue forms in the aisle: You only get up for the loo if your Loo-Q button goes green. Rule 3 says this only happens if:
- The message "$t: S_i\mbox{ needs loo}$" is first in your local queue, $Q_i$; and
- Your seat has received a message from every other seat with a timestamp later than $t$.
- A receipt of your loo request – indicating their queue is synchronised with yours, and you're good to go to the loo; or
- Their request for the loo, in which case:
- If their request is timestamped later than yours, then your position is unchanged and you are good to go to the loo; or
- If their request is timestamped earlier than yours then you get bumped from the front of your local queue and you'll have to wait until they've finished, at which point they'll send you a finished message timestamped later than your request.
So your button only goes green once everyone requesting the loo earlier than you has been to the loo (Rule 3) and has returned to their seat and sent their finished messages (Rules 4 and 5). No queue forms in the aisle.
The Loo-Q system is fair, requests for the toilet are granted in the order in which they are made: Again, the second part of Rule 3 guarantees this.
Everyone who has requested the loo will eventually get to go (up to the point the plane begins its descent for landing): Everyone who goes to the loo has to return to their seat (so the drinks trolley can get through), so their Loo-Q button will eventually turn off, their finished messages will be sent and their request will be removed from all the local queues. So, given enough time, each request will eventually reach the front of their queue and pass Rule 3.
No need to talk to anyone – you get to stay in your seat watching your movie for as long as possible: This final specification is satisfied thanks to the wonder of the distributed nature of this algorithm. Hooray for distributed algorithms and hooray for Leslie Lamport and his logical clocks!
You can see a worked example, showing the Loo-Q system in action for three of the seats on a plane, here.
About this article
This article is part of our Stuff happens: the physics of events project, run in collaboration with FQXi. Click here to see more articles and videos about the role of events, special relativity and logical clocks in distributed computing.
Rachel Thomas is Editor of Plus. She interviewed Leslie Lamport in September 2016 at the Heidelberg Laureate Forum.