Clocks: What does that word make you think of? A traditional clock face with the hour, minute and second hands ticking past thanks to the power of cogs and springs? The miracle clock in your smart phone that maintains its accuracy and resets to the local time when you travel overseas thanks to a time server on the internet? Or the vibrations of a cesium atom defining the internationally accepted measurement of a second (one second is 9,192,631,770 cycles)?

Time is relative

All of these things, all clocks, are really just a way of assigning a number to an event, representing the time that event occurred. As we saw in the last article, Violating Causality, time is personal. In Einstein's special theory of relativity, the time at which things occur, and indeed the order in which things occur can vary for different observers. And in distributed systems (as we saw in the article Distributed systems and ambiguous histories), while the timeline of history is clear-cut for a particular process, it can be ambiguous for events that happened in different processes. Both of these things mean that the events in a distributed system, and the events in spacetime, are only partially ordered by the notion of "happened before".

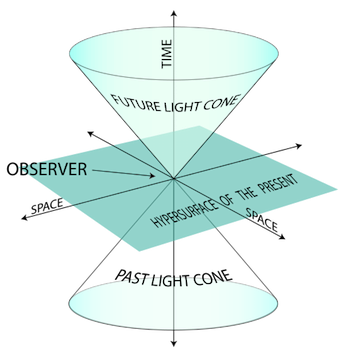
Only the events in the past light cone can effect us (the observer, represented in a simplified spacetime where space is two-dimensional and time is one-dimensional), and we can only effect events in our future light cone. (Image by K. Aainsqatsi CC BY-SA 3.0)

What is certain, in special relativity at least, is causality, the relationship between events that can influence each other. (Remember that in special relativity an event is a point in spacetime, having three coordinates specifying its location in space and one coordinate specifying its location in time.) As nothing moves faster than the speed of light, an event A can only effect an event B if a signal, a flash of light, sent from event A could reach the spatial coordinates of event B, before event B occurs. This defines what's called the future light cone of an event (similarly a past light cone), consisting of all those points in spacetime that a light beam could reach if it was emitted from A.

Within the future and past light cones of A spacetime is totally ordered by the notion of "happened before". The order in which events occur is unambiguous, causality has solved the problem. (Note that comparing event A to events outside its light cones can lead to ambiguity, headaches and dizziness – so this is not recommended.) There still may be a bit of stretchiness within the light cones as far as the time at which events occurred, depending on different observers, but the order of the timelines is clear.

Clocks to the rescue

When Lamport read a paper by Bob Thomas and Paul Johnson in 1975 he realised that the way they described their distributed system meant that a "violation of causality" was possible. "That is to say one operation [in the distributed program] that happened before another, would have been executed as if they had occurred in the opposite order," says Lamport.

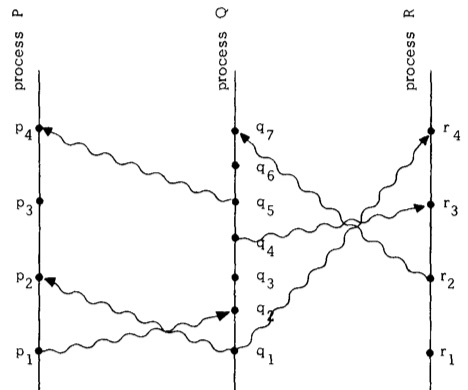A spacetime diagram of a distributed system made up of three processes P, Q and R.

This is possible because the events in a distributed system are only partially ordered. For example, in our spacetime diagram of the distributed system of the processes P, Q and R, it isn't clear if the event $p_4$ happened before event $r_1$ or visa versa – they are concurrent. Our distributed program might assume the operation at $r_1$ is executed first, but as the two events are concurrent it is possible that they happen in the opposite order. Lamport realised the solution was to take the partially ordered set of events and impose a total order.

Your first instinct might be to say that an event A happened before an event B if A happened at an earlier time than B, and you can just rely on real time, measured by a real physical clock, to decide this. But, says Lamport, it is sometimes necessary to make sure a system runs correctly only in terms of what can be observed inside that system – so you might have to do without real clocks. "And even if you do have real clocks, they may not be perfectly accurate or perfectly synchronised."

Instead, to totally order the events Lamport defined a new type of clock, a logical clock, which allowed him to define a total ordering on any distributed system. "These are not clocks keeping real time, they're just counters, but you can use them as time," says Lamport. "And you can use that clock ordering to order all the events in the distributed system and get a linear ordering of them, [a global timeline] that preserves causality. The order is there, recording the history of everything that happens."

Local time

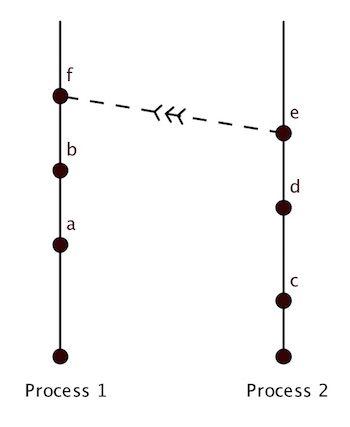
A distributed system consisting of two processes, who's individual histories are shown as vertical lines with time going up. The message sent from one process to another is indicated by a dashed line.

To understand Lamport's algorithm for implementing these logical clocks, consider a distributed system consisting of two processes $P_1$ and $P_2$, each consisting of a sequence of events. At each location, that is, for each process, there is a local clock that "ticks" (moves forward by 1) between events. As we'll see, the value of the clock might change more than once between events, so the changing of the value, the ticking, doesn't itself constitute an event.

"The basic rule for maintaining these clocks is that, first of all, whenever an event happens at a place [within a process] that local clock gets advanced, so you don't have two events at the same place happening at the same time."

The total order on the behaviour of the distributed system is created by creating a global history of all the events that have occurred, across all the different processes. This is done by ordering all the events according to the times on their local clocks.

In order for this to be a total order, so that any event has a clear and unambiguous place in the timeline, no two clocks at different places can ever show the same time. To ensure this, the values of a local clock has a decimal place at the end that identifies the clock's location.

So the initial value of the clock $C_1$ for process $P_1$, when the process starts, would be $C_1(\mbox{start})=0.1$. And each time an event happens within $P_1$, without any interaction from $P_2$, the clock advances by 1 tick: $$ P_1: C_1(\mbox{start})=0.1 \rightarrow C_1(\mbox{event a})=1.1 \rightarrow C_1(\mbox{event b})=2.1. $$ Similarly for process $P_2$: $$ P_2: C_2(\mbox{start})=0.2 \rightarrow C_2(\mbox{event c})=1.2 \rightarrow C_2(\mbox{event d})=2.2. $$ You can see how encoding the location of each processor as a decimal place in each local clock results in the two local clocks never showing the same time.

At this point the global history (the sequence of events as described by the global clock $C$) of our distributed system would be: $$ \begin{array}{ll} & C(P_1\mbox{ start})=0.1 \\ \rightarrow & C(P_2\mbox{ start})=0.2 \\ \rightarrow & C(\mbox{event a in }P_1)=1.1 \\ \rightarrow & C(\mbox{event c in }P_2)=1.2 \\ \rightarrow & C(\mbox{event b in }P_1)=2.1 \\ \rightarrow & C(\mbox{event d in }P_2)=2.2 \end{array} $$

Asking the time

So far the processes have not interacted. But if they never interacted we wouldn't have a distributed system, just two processes doing entirely disconnected work side by side. In a distributed system the processes send messages to each other, possibly influencing future events in the system.

When a process sends a message, say $P_2$ sends a message to $P_1$, that counts as an event for that process, $P_2$. So $P_2$'s local clock would advance by 1 and the message sent would be timestamped with this new local time. So picking up where we left off... $$ P_2: C_2(\mbox{event d})=2.2 \rightarrow C_2(\mbox{send message to }P_1)=3.2 $$ and the message sent to $P_1$ would be timestamped with the value 3.2.

"The other part of [the rule for maintaining these clocks], the part that Johnson and Thomas missed, is that when you receive a message you have to advance your clock so it's both later than its previous value and later than the value attached to the message you've just received," says Lamport.

When a process receives a message, this also counts as an event in that process. So when process $P_1$ receives the message from $P_2$, timestamped with the global time $C=3.2$, it must advance its local clock, and here is where Lamport's great insight comes in.

Picking up where we left off for $P_1$: event $b$ had just occurred at time $C_1=2.1$. When $P_1$ receives the message, it needs to advance its local clock $C_1$. If $P_1$ advances its clock by 1, the local time at $P_1$ would be $C_1=3.1$, but this would be less than the time, $C=3.2$, timestamped on the message. If we said $P_1$ received this message at a time of $C=3.1$, that would put it earlier in the global history of the distributed system than the time $C=3.2$ when $P_2$ sent the message – $P_1$ would have received the message before it was sent! So $P_1$ must advance its clock $C_1$ by 2: making the local time $C_1=4.1$, later than the time attached to the message, and in the global history putting the event of receiving the message after the time that the message was sent.

So the local history for the process $P_1$ would continue on as follows: $$ P_1: C_1(\mbox{event b})=2.1 \rightarrow C_1(\mbox{receive message from }P_2\mbox{ timestamped }C=3.2)=4.1. $$ And so the whole global history of our distributed system would be: $$ \begin{array}{ll} & C(P_1\mbox{ start})=0.1 \\ \rightarrow & C(P_2\mbox{ start})=0.2 \\ \rightarrow & C(\mbox{event a in }P_1)=1.1 \\ \rightarrow & C(\mbox{event c in }P_2)=1.2 \\ \rightarrow & C(\mbox{event b in }P_1)=2.1 \\ \rightarrow & C(\mbox{event d in }P_2)=2.2 \\ \rightarrow & C(P_2\mbox{ sent message to }P_1)=3.2 \\ \rightarrow & C(P_1\mbox{ received message from }P_2)=4.1 \end{array} $$

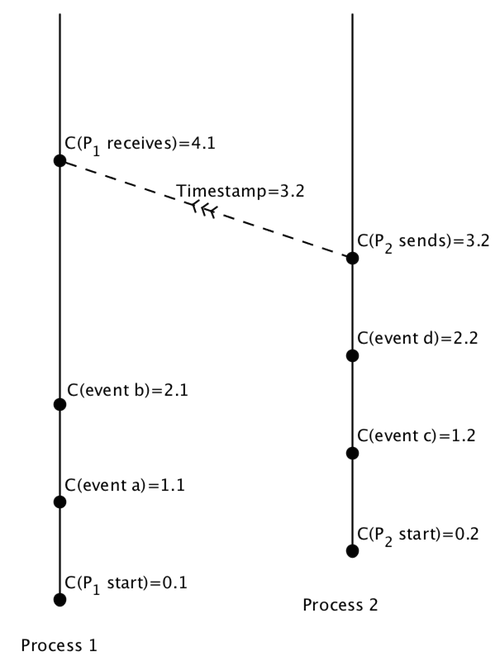
The spacetime diagram of our system, ordered by Lamport's logical clocks

History is written

"That's the whole algorithm," says Lamport. And with these simple rules Lamport was able to totally order any distributed system, creating unambiguous timelines that ensure that causality is never violated.

His paper Time, clocks, and the ordering of events in a distributed system introduced a new rigorous way of approaching distributed computation and is one of the most cited papers in computer science. Although Lamport recalls two contrasting reactions to the paper when it was first published: "Some people thought that it was brilliant, and some people thought that it was trivial. I think they're both right."

"I realised that being able to totally order the events gave you the power to implement anything you wanted in a distributed system," Lamport says. The impact of Lamport's work was recognised in 2013 with the Turing Award, considered the Nobel Prize of Computer Science, and we all benefit from his work every day. "The Internet is based on distributed-systems technology, which is, in turn, based on a theoretical foundation invented by Leslie [Lamport]," says computer scientist Bob Taylor, one of the pioneers of the Internet. "So if you enjoy using the Internet, then you owe Leslie."

You can see Lamport's logical clocks algorithm working in detail in this example.

About this article

This article is part of our Stuff happens: the physics of events project, run in collaboration with FQXi. Click here to see more articles and videos about the role of events, special relativity and logical clocks in distributed computing.

Rachel Thomas is Editor of Plus. She interviewed Leslie Lamport in September 2016 at the Heidelberg Laureate Forum.