Maths in a minute: Algebraic varieties

Intuitively, an algebraic variety is a geometric shape defined by a certain type of equation. A simple example is a straight line. As you might remember from school, the equation

$y=2x+1$

describes a line of slope $2$ which intersects the vertical axis of a standard Cartesian coordinate system at the point $(0,1)$ . All the points in the plane whose coordinates $(x,y)$ satisfy the equation lie on this line, and vice versa.

Similarly, the equation

$x^2+y^2=1$

describes a circle of radius 1 around the point $(0,0)$ in our coordinate system. (This follows from Pythagoras’ theorem, see the figure below).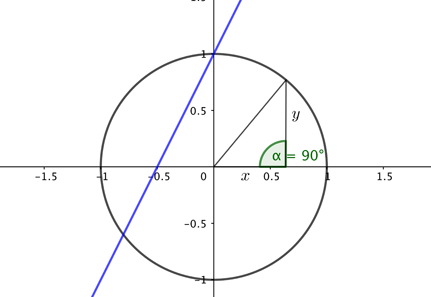

The blue line has equation y=2x+1 and the circle has the equation x²+y²=1.

The fact that algebra and geometry tie together in this way is really quite marvellous. We take it for granted today, but the connection was only spotted in the 17th century, when the French mathematician René Descartes developed the Cartesian coordinate system, which is named after him, reportedly while lying in bed (read more here).

The circle and the line are both examples of algebraic curves in the Euclidean plane: curves that are defined by algebraic equations. Going up a dimension, we can also consider algebraic surfaces. The sphere in 3D Euclidean space that is centred on the point $(0,0,0)$ and has radius $1$ is an example. In analogy with the circle in the dimension below, it's given by the algebraic equation

$x^2+y^2+z^2=1.$

As you might already expect a plane in 3D space is another example of an algebraic surface.

But we don't need to stop here: more complicated polynomial equations, perhaps defined over other classes of numbers (for example complex numbers), give rise to the general notion of an algebraic variety. Algebraic curves and surfaces are examples of algebraic varieties, but in general algebraic varieties can be much more complicated: they can even exist in higher dimensions which can't be visualised. That's not something that deters mathematicians, however, because they've long developed a way of doing geometry even when they there are too many dimensions to imagine (find out more in this short article).

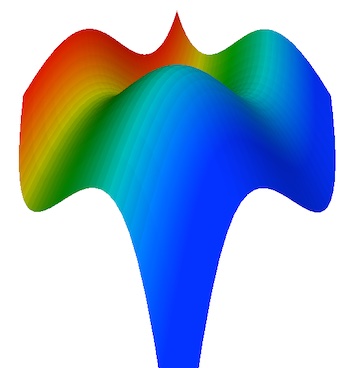
This surface is defined in a three-dimensional coordinate system by the equation z=x³+y³+1.

The area of maths that studies geometry using algebra is called algebraic geometry. A lot of mathematical effort has gone into classifying algebraic varieties: sorting them into families of varieties that are all alike in some way. The Fields Medal, one of the most prestigious prizes in maths, has been awarded for work in this area a number of times. One example is the work of Caucher Birkar, who won a Fields Medal in 2018. You can read about it in this article.

In this context there’s an interesting observation to be made. To illustrate it, suppose you’re looking at the family of all straight lines that pass through the point $(0,1)$ in a Cartesian coordinate system (this family includes our line above). Each such line is defined by its slope. This can be any number between $0$ (corresponding to a horizontal line) to infinity (corresponding to a vertical line). The slope can be positive (so the line is sloping upwards) or negative (it slopes downwards). Thus, every line in our family can be indexed by a unique number between minus infinity and plus infinity. Conversely, every number between minus infinity and plus infinity indexes a unique line in our family.

The numbers that lie between minus and plus infinity, our index set, themselves line up to form a line. This means that our family of algebraic curves (lines through $(0,1)$ ) is described by a set of indexes which itself can be viewed as an algebraic curve. Something similar can also be true for more complex algebraic varieties: entire families of them can be indexed by sets of objects that themselves can be viewed as algebraic varieties. This self-referential nature of algebraic varieties provides a useful tool for studying and classifying them.

For a more technical definition of algebraic varieties, see Wikipedia.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.