
The Fields Medal 2018: Caucher Birkar

Caucher Birkar has been awarded a Fields medal for his contributions to a field of maths called algebraic geometry. The area does exactly what its name suggests: it tries to understand geometric objects using equations that describe them.
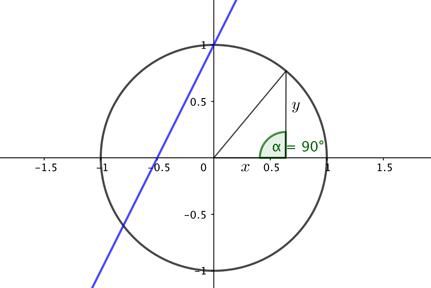
It's an idea you might be familiar with from school. The equation
$y=2x+1$ describes a line of slope $2$ which intersects the vertical axis of a standard Cartesian coordinate system at the point $(0,1)$. Similarly, the equation $x^2+y^2=1$ describes a circle of radius 1 around the point $(0,0)$ in our coordinate system. (This follows from Pythagoras' theorem, see the figure).
The circle and the line are both examples of algebraic curves in the Euclidean plane: curves that are defined by algebraic equations.
Going up a dimension, we can also consider algebraic surfaces. The sphere in 3D Euclidean space that is centred on the point $(0,0,0)$ and has radius $1$ is an example. In analogy with the circle in the dimension below, it's given by the algebraic equation $$x^2+y^2+z^2=1.$$ As you might already expect a plane in 3D space is another example of an algebraic surface.
But we don't need to stop here: more complicated polynomial equations, perhaps defined over other classes of numbers (for example complex numbers), give rise to the general notion of an algebraic variety. Algebraic curves and surfaces are examples of algebraic varieties, but in general algebraic varieties can be much more complicated: they can even exist in higher dimensions which can't be visualised. That's not something that deters mathematicians, however, because they've long developed a way of doing geometry even when they there are too many dimensions to imagine.
Given the infinite zoo of algebraic varieties that exists, a good idea is to try and classify them into families, just as one would classify a collection of butterflies. Going back to our simple example above, you might want to classify them according to the type of their shapes: things that are like planes go into one family, things that are sphere-like go into another, and so on.
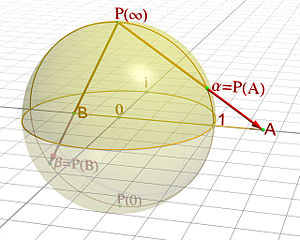
The stereographic projection relates each point of a sphere (apart from the one right at the top) to a point on its equatorial plane: for each point p on the sphere (apart from the one at the top) draw the line that connects it to the point right at the top. That line will intersect the equatorial plane at some point q. Image: Jean-Christophe Benoist.
But you might also allow yourself a little more flexibility. The projection shown in the figure on the left shows how a sphere minus a point can be turned into a plane: for each point p on the sphere, apart from the North pole at the top, draw the line that connects p to the North pole. That line intersects the equatorial plane at some point q. In this way every point p on the sphere (apart from the North pole) can be moved to a point q on the plane, so our projection transforms the sphere minus one point into a plane. So it seems that the plane and the sphere are distantly related after all, and we might keep this in mind when classifying algebraic surfaces into families.
The projection we've just considered is an example of a birational map. Birational maps are defined in a much wider context and can be used to link up more complicated algebraic varieties than just spheres and planes. And there are good reasons for why we might link them up in this way. One is that not all algebraic varieties are as nice and smooth as the planes and spheres we thought about above. Some have singular points; loosely speaking pointy cusps. At least when you are dealing with algebraic varieties of a certain type (technically over a field of characteristic 0), the flexibility of birational maps allows you to link such a singular variety to a smooth projective variety without any singular points. Being able to "resolve" varieties in this way is a very useful tool, so there really is some sense in considering varieties that are birationally related as being part of the same family.
Birkar works in the area of birational geometry which is all about classifying algebraic varieties in this way. In particular, mathematicians hope to show that every (projective) algebraic variety is birationally related to a particularly nice kind of variety that is made up of three basic building blocks. For the simplest types of varieties (of complex dimension one) this was already shown by the mathematician Bernhard Riemann at the end of the nineteenth century. Dimension two was sorted out the beginning of the twentieth century. Dimension three only followed suit a long time later, between the 1970s and the 1990s. Dimensions four or greater still pose major problems, however, and it's in this area that Birkar has made major contributions. The aim is to show that something called the minimal model programme, an algorithm designed to transfer a variety into one of the three nice building blocks mentioned above, really does work.
Birkar was born in 1978 to farmers in the Kurdistan Province of Iran, and went to school during the turmoils of the war between Iran and Iraq. "[War-ridden] Kurdistan was an unlikely place for a kid to develop an interest in mathematics", commented Birkar in his acceptance video shown at the ICM opening ceremony in Rio. It was his brother who taught him higher level maths that he didn’t encounter at school, and eventually he studied maths at the University of Tehran. In 2000 he moved to England where he was eventually granted refugee status and completed his PhD. He is now a Professor at the Department of Pure Mathematics and Mathematical Statistics at the University of Cambridge. This makes him our neighbour, so we're particularly proud of his amazing achievement. Congratulations Caucher Birkar!
This content was produced in a collaboration with the London Mathematical Society. With kind support from the Institute of Mathematics and its Applications.

