Maths in a minute: Random walks
In mathematics a random walk (also called a drunkard's walk) is a succession of random steps.
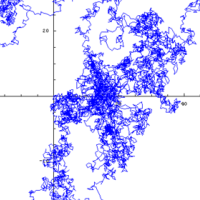
You can generate a random walk quite easily by placing yourself in the middle of your garden or local park. Pick a random direction and walk one step in that direction. Then pick another direction at random and walk one step in that direction. And so on. The result, traced on a map, will look something like this:
10,000 steps of a random walk generated on a computer. Image: Zweistein~commonswiki, CC BY-SA 3.0 DEED.
Similar random motion occurs in nature, for example with particles suspended in a liquid or gas. This was first observed in 1827 by the botanist Robert Brown, while looking through a microscope at pollen immersed in water. It's therefore called Brownian motion. The process described above, transposed into three dimensions and phrased in the language of maths, gives a mathematical model of Brownian motion.
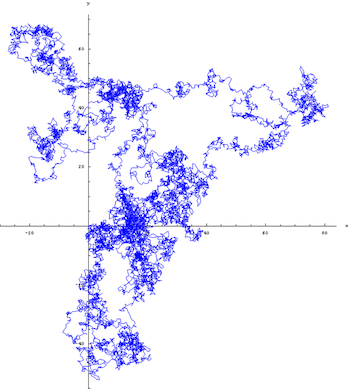
Variations on the theme above can lead to interesting models of other natural processes. Imagine that at each stage you don't only choose the direction at random, but also the distance you travel into that direction (so it's not just one step). However, you rig your random number generator in such a way that short distances are more likely to be picked than longer ones.
The paths that result from these rules look like Brownian motion interspersed with long distances travelled in one direction only. That's because, even though long distances are less likely to be picked than shorter ones, they are still likely enough to get picked occasionally.
1,000 steps of a Lévy walks generated on a computer.
These kinds of random walks are called Lévy walks, and are similar to what you see when you let your dog off the lead in a park. It'll sniff out a small patch, then dash off in a random direction to sniff out another patch, and so on. Indeed, a seminal paper published in 1999 suggested that Lévy walks provide the best strategy for searching for things that are sparsely distributed in space, like interesting tidbits a dog might be looking for in a park. The suggestion is that dogs, as well as many other animals that have been observed to move in this way, have evolved this behaviour as an optimal foraging strategy, although the theory remains controversial. You can find out more in this article.
Another variation are reinforced random walks, where steps are more likely to be taken so as to follow paths that other "walkers" have taken before. This can be used to model, for example, the ants who lay down trails of pheromones which attract other ants. In a self-avoiding random walk it is not allowed to take steps that would lead to the path crossing itself. Self-avoiding random walks play an important in the study of chain-like structures such as polymers (find out more in this article).
In summary, random walks are great for modelling motion, be it of particles, animals, or even people. They are great for mathematical exploration — it's quite easy to construct your own random walks and play around with the results you get, but understanding their overall structure can quickly bring you up against some hard maths. The patterns you see emerge when playing with random walks can be surprising and beautiful (you may even hit upon a fractal). If you like to play with freedom and constraint, then random walks are for you!
This article forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
