
Maths takes flight at the Science Museum
We have several images of the week this week! And they all come from the beautiful design for the new maths gallery that will open at the Science Museum in London in 2016. The first is the inspiration that Zaha Hadid Architects used for the layout of the gallery. It's the turbulence field of an aircraft which captures how the air moves around it. This is mathematically described by the Navier Stokes equations, which apply in many different situations, from modelling the weather to understanding how blood flows. (You can read more about the Navier Stokes equations in Universal pictures and turbulence in Understanding turbulence.)
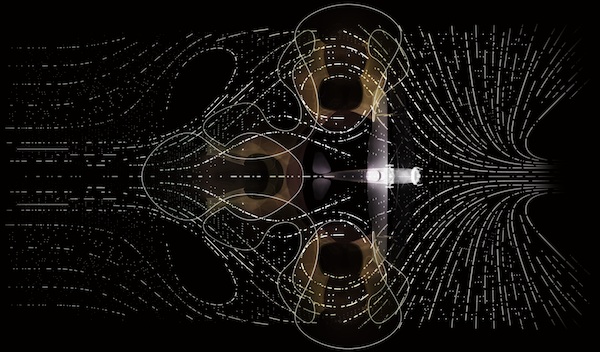
A top view of the turbulence field around the Handley Page aircraft, one of the main exhibits in the new maths gallery (Image courtesy of Zaha Hadid Architects)

The Handley Page Gugnunc in flight
The plane that will hang in the centre of the gallery is a Handley Page Gugnuncs. This experimental plane was designed for the Guggenheim Safe Aircraft competition in 1929 which aimed to find planes that could fly safely at slow speeds and with short takeoffs. The research beind the plane profoundly advanced aviation technology and understanding at the very beginnings of civilian air travel. (You can read two brilliant articles from the 1930s about the competition and the aircraft itself.)
Behind the plane are three minimal surfaces (surfaces with the smallest possible area that satisfy some constraints) that are based on the shapes of the vortices in the turbulence created behind the plane in flight. The equation defining these $$ \begin{array}{l} a_1 sin(x)sin(2y)sin(3z) \\ + a_2 sin(2x)sin(y)sin(3z)\\ +a_3 sin(2x)sin(3y)sin(z)\\ +a_4 sin(3x)sin(y)sin(2z)\\ +a_5 in(x)sin(3y)sin(2z)\\ +a_6sin(3x)sin(2y)sin(z)=0 \end{array} $$
The design or the Handley Page exhibit in the new maths gallery
is a complicated looking combination of familiar sine functions that is governed by six different parameters. By varying the values of these parameters, the $a_i$, the surface bends and twists producing a whole family of different shapes. Some of these will be created will be created in physical form to provide the support display cases used throughout the galleries. You can play with these surfaces yourself or just watch their creation in the video below.
It is thrilling to see such a striking, beautiful and mathematical design for the gallery. But of course the real strength will be the exhibits themselves. These will span 400 years of science and mathematics with objects ranging from hand-held mathematical instruments from the renaissance to modern technology. We all know that maths is the language of the universe and we can't wait to see what stories we'll find in the new maths gallery when it opens in 2016.
You can find out more about the gallery at the Science Museum