
Universal pictures
Parts of this interview are also available as a podcast.
"At first mathematics and photography were completely separate things to me," says Peter Markowich. "But then, when I was looking through my pictures one day, I realised that behind many of them there is a mathematical story to tell. I started to look at the pictures in terms of the mathematics that describes them. And then it all came together."

Sunset in a dune field, Sossus Vlei, Namibia. Photo: Peter Markowich.
Markowich is Professor of Applied Mathematics at the University of Cambridge, and specialises in the applications of partial differential equations, or PDEs. Terrifying though they may sound, these equations are bread and butter objects for anyone who uses maths to solve real-life problems. This is because they describe change: "Partial differential equations relate physical variables, like mass, energy and velocity, to their variation with respect to more elementary variables, like time and position."
Change is what characterises most things in the world: motion is a change in position over time, growth is a change in size over time, etc. Mathematical descriptions of physical systems are therefore typically phrased in terms of rates of change — derivatives in maths speak. A differential equation is an equation involving the derivatives of a function, and solving it amounts to finding the function itself. See here for a little more detail.
Turbulence

Iguassu Falls, border of Brazil and Argentina. Photo: Peter Markowich.
Turbulence in liquids and gases is an extremely complex phenomenon. "What is turbulence? It's basically a mixture of all scales," explains Markowich. "When you think of [water flowing smoothly down a channel] you observe just one scale: the average velocity of the flow. With a turbulent flow the situation is completely different. When you measure the velocities at locations that are very close to each other, you get completely different values. There are great problems in the numerical simulation of turbulence, because you can't restrict to one scale or two scales, you have to cover all of them."
Despite this complexity, scientists believe that turbulence is described to a reasonable level of accuracy by a very famous set of PDEs, known as the Navier-Stokes equations. When trying to describe the motion of a liquid or gas, what you're after are the velocity $v(x,y,z,t)$ and the pressure $P(x,y,z,t)$ of the liquid at point $(x,y,z)$ in space and at time $t$. The Navier-Stokes equations, named after the physicists Claude-Louis Navier and George Gabriel Stokes, are a set of coupled PDEs that relate changes in velocity, changes in pressure and the viscosity of the liquid. To find the functions $v$ and $P$, you have to solve these equations.
But that's no easy feat. Exact solutions to the equations — solutions that can be written down as mathematical formulae — exist only for simplified problems that are of little or no physical interest. For most practical purposes, approximate solutions are found through computer simulations — essentially through educated guess-work — that require immense computing power.
The Navier-Stokes equations
At a point (x,y,z) in space, the velocity v(x,y,z) has three components (u,v,w), one for each co-ordinate. The pressure of the liquid is P(x,y,z). Take a deep breath. Here are the equations: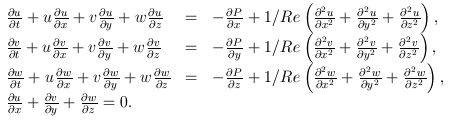
The parameter Re in the equations is called the Reynolds number and measures the viscosity of the liquid.
Differential equations have a habit of being hard to solve, but with the Navier-Stokes equations there is an additional problem that makes numerical difficulties pale into insignificance: no-one knows if exact mathematical solutions even exist in all three-dimensional cases involving an incompressible liquid. And if they do exist, we still don't know if they involve oddities, such as discontinuities or infinities, that don't square with our intuition of how a liquid should behave.
This might seem strange, even scary, given that the equations are used all over the place, all the time — meteorology and aircraft design are just two examples. The fact is that, in the cases we can compute, approximate solutions do seem to give an accurate description of the motion of fluids. What we don't know is what, if anything, the model given by the Navier-Stokes equations tells us about the exact nature of fluid flow.
"Many things could happen," says Markowich, "The theorem [that there exists a physically reasonable solution] could be true, or it could be false. In that case we have to re-think our model, or our intuition of nature." But even if the theorem turned out to be false, this would not render existing methods to model aerofoils or space craft useless overnight. "In practice, things are done by numerical computations. Very often we do observe very large velocity fields, and they could correspond to mathematically infinite ones. But people know how to deal with large velocity fields that occur locally. I don't think [the theorem being false] would change a lot in an engineering context. But it may very well change our conception of fluid flow." (You can find out more about computational fluid dynamics here.)

Plane taking off from Rio de Janeiro's City Airport. Photo: Peter Markowich.
At the moment, mathematicians are divided over the answer to the problem. "If you ask my guess," says Markowich, "I would say there is a 50:50 chance that the theorem is true — I just don't know. People have tried every available technique to solve the problem. Progress has been made, but it's very slow. My feeling is that if we do not develop completely new techniques, we will not see a solution."
It's these immense difficulties that have turned the understanding of the Navier-Stokes equations into one of the seven Millennium Problems posed by the Clay Mathematics Institute. Whoever proves or disproves the existence of finite and smooth solutions is set to earn a million dollars.
You can find out more about the Navier-Stokes equations and other Clay Millennium problems in the Plus article How maths can make you rich and famous.
Spots and stripes
When it comes to animal patterns, nature regularly outdoes herself. In this area too, it's PDEs that best describe what's going on. "The basic idea behind this is that cells migrate towards certain parts of the animal skin," says Markowich, "The migration is controlled by chemical sensing: the cells sense a chemical that tells them where to go, and that generates the pattern."

Giraffe coat. Photo: Peter Markowich
Interestingly, the mathematical model which describes this process was devised by the father of modern computer science, Alan Turing. "Turing wrote down a system of what we now call reaction-diffusion equations. He observed that, if you tune the parameters correctly, the solutions resembled animal skin patterns."
Turing was looking at systems comprising of two components that can react with each other and diffuse. Let's imagine that these two components are chemicals living in the skin of an animal embryo. One of them is an inhibitor, which suppresses the production of both itself and the other chemical, and the other an activator, which promotes the production of both chemicals. At any time $t$ and any point $x$ on the embryo, the concentrations of the activator and inhibitor are given by $A(x,t)$ and $I(x,t)$ respectively. Of course, these concentrations change over time due to new production (a reaction) and diffusion. The changes of concentration of activator and inhibitor over time can be written down as partial differential equations involving the derivatives of both $A$ and $I$ with respect to time.

Australian salt water crocodile. Photo: Peter Markowich
Initially (when $t=0$), the two chemicals are in equilibrium - their concentrations do not change over time. The amount of activator and inhibitor is just right so that the reaction and diffusion rates exactly balance. The situation is an unstable equilibrium, however, and the slightest nudge knocks the system away from this equilibrium.
Animal pattern equations
For the sake of simplicity, imagine the embryo as a one-dimensional line and look at the concentration of each of the two chemicals at each point x along the line. Here are the equations:
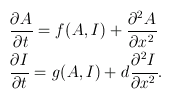
The first term on the right-hand side of each equation describes how much activator/inhibitor is being produced. These terms are functions of activator and inhibitor concentrations because they both affect the reaction rate.
The second term in each equation is a second derivative describing how quickly the gradient of activator/inhibitor is changing. These terms give the rate of diffusion.
The extra term, d, on the right-hand side of the second equation is the diffusion coefficient — how much quicker the inhibitor diffuses than the activator. The inhibitor being a faster diffuser was shown by Turing to be pivotal in driving the process of pattern generation.
Once the system is knocked off its equilibrium poise, a snowball effect sets in as activator and inhibitor react and diffuse. If the parameters that govern the diffusion of each component are just right, then we end up with a polarisation: the symmetry of the uniform concentration is broken into roughly evenly spaced regions of, for example, high activator. If the activator also promotes the generation of a pigment in the skin of the animal, then this pattern can be made visible.
Turing was studying two-component systems in general, rather than animal patterns in particular, but once he saw that his solutions resembled them, he came up with the theory we just described. "Now these chemicals have actually been found in animals," says Markowich, "So the theory that was originally purely descriptive might become biologically founded." But even if the model is not confirmed biologically, there are applications: these days computer programmers use Turing's reaction-diffusion equations to generate realistic looking animal coat patterns in real time.
You can find out more about Turing's model in the Plus article How the leopard got its spots.
Down the river
In the late eighteenth century the French civil engineer Gaspard Monge was considering the unglamorous problem of how to best shift a pile of building rubble into a hole. "He was trying to figure out how to do this in an optimal way," explains Markowich, "Start shovelling on the left side, or the right side? It turned out that, mathematically, finding the optimal way was a pretty hard job."

Branching river, South Eastern Australia. Photo: Peter Markowich
Since Monge's original calculations, the theory of optimal mass transportation has come a long way, not just mathematically, but also in terms of its applications. It was revolutionised during the second world war by the Russian mathematician Leonid Kantorovich. "After another twenty years it became clear that there is a deep connection between optimal transportation theory and partial differential equations. Solving the optimal transportation problem is equivalent to solving a very complicated, fully non-linear PDE."
Optimal transportation principles have been used to model the branching of rivers, trees, and the veins within a leaf, and they have even been applied to urban planning. In each case, something is transported somewhere else in an optimal way: water in rivers, nutrients and water in trees and leaves, and people or resources in the case of urban planning. "The mathematical tools that solve all these problems, be it the original Monge application, or nutrient distribution in leaves, or the optimal construction of cities, are very similar. Of course reality is much more complicated [than assumed in the theory], but still we can learn a lot from these rather simple mathematical models."

Urban planning (or lack of it) in Quito, Ecuador. Photo: Peter Markowich
People
Human behaviour is one of the few aspects of life that hasn't yet been properly explored by PDEs. But, as Markowich explains, that's in the process of changing. "This is based on what I think is a very clever recent idea, and that is applying principles of statistical physics to human interaction. Think of a gas, for example air. How is transport in a gas effected? Basically, a gas is collision driven: atoms in a gas collide. In some sense they collide as billiard balls do. If you observe two atoms, they go into a collisional event with certain velocities and come out of it with other velocities. But you can relate the outgoing velocities to the incoming velocities in a very clear way."

Opinion forming on the Zocalo, Mexico City. Photo: Peter Markowich
The behaviour of atoms in a gas is described by the Boltzmann equation of gas dynamics. What you're after in this context is a distribution function $f(x,p,t)$, which gives you, at each time $t$, the number of atoms with position $x$ and momentum $p$. In the late nineteenth century, the Austrian physicist Ludwig Boltzmann, based on ideas of James Clerk Maxwell, developed an equation describing the evolution of this distribution function — its change over time — in terms of atom collisions and other forces acting on the gas. "Now if you think of human interactions, you can imagine that things like opinion forming is driven by pairwise interactions between individuals," says Markowich. "We meet and discuss something, and generally we come out of a discussion with slightly changed opinions. So you can build a theory of opinion formation based on microscopic 'collisions'. What comes out, not too surprisingly, is a Boltzmann-type equation, which models the evolution of opinions in human society."
The Boltzmann equation
The Boltzmann equation is $$\frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} \cdot \frac{p}{m} + \frac{\partial f}{\partial p} \cdot F = \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}}$$ The function $F(x, t)$ describes the force field acting on the particles, and $m$ is the mass of the particles. The term on the right hand side describes the effect of collisions between particles.
"Of course, there are many things that have to be taken into account. We know that opinions are influenced by external forces, like the presence of media or of strong leaders. But all this can be built into the model, and what comes out is pretty reasonable." These models have been tested against reality and performed quite well. In fact, models like these are now being put to practical use. "I have been to UCLA recently and there was a working group of mathematicians, sociologists, a psychologist, and the police, working on crime modelling in LA. How do the gangs behave, how do they diffuse, how does crime spread, and so on. In the last ten years mathematics has also started to hit the sociological sciences."

Opinion forming in Isfahan, Iran. Photo: Peter Markowich
Erotic art
Telling the mathematical story behind an image is one thing. Quite another is using mathematics to reconstruct a damaged image, and this is something Markowich himself has been working on. "It's an interesting story. There is a wall fresco from the late medieval period which was rediscovered about thirty years ago in an old house in Vienna. The house originally belonged to a rich Jewish merchant who had the fresco painted. The image contains some pretty [explicit] sexual connotations. Two hundred years later the house was bought by the catholic church, who didn't like that idea." Rather than destroying the fresco, however, the new owners glued a plaster wall over it. And when this wall was removed, parts of the fresco came off with it.

Part of the Neidhart frescoes. Photo courtesy Andrea Baczynski.
"The question that arises is how to restore the fresco. Of course there is classical restoration work done by artists who paint into it physically. The idea we had was to use modern techniques of image processing." Central to this is again the concept of diffusion. Think of a black-and-white digital image made up of a number of pixels, each with co-ordinates $(x,y)$. Each pixel comes with a numerical greyvalue $u(x,y)$. Those pixels that lie in a hole in the picture, where information is missing, are white. Now think of diffusion as migration of information from one pixel to its neighbouring pixels. The diffusion equation, applied to regions containing holes, can model the evolution of the system over time. Eventually, the holes are filled in, based on a "best guess", using information from neighbouring pixels. Loosely speaking, the grayvalues inside the holes are constructed by averaging the grayvalues located around the holes. This is the naive approach, but, using more complicated equations, it can be made more sophisticated and also applied to colour images.
The diffusion equation
Let $u(x,y,t)$ denote the greyvalue of the pixel with co-ordinate $(x,y)$ at time $t$ of the diffusion process. The diffusion equation is $$\frac{\partial u(x,y,t)}{\partial t} = \frac{\partial^2u(x,y,t)}{\partial x^2} + \frac{\partial^2u(x,y,t)}{\partial y^2}.$$
"Of course no mathematical technique can predict with 100% certainty what was in a hole in a fresco. There's no way to make sure you deduce exactly what the artist had put in, but there are good indications. You use the surrounding information in a mathematically consistent way." The fresco in question has already been physically restored, but Markowich and his team are aiming for more general applications. "There are other frescoes, which may not even be touched by the restorators because they are too valuable. Here the idea would be that in the same room as the unrestored frescoes, you have computers running, which generate virtual restorations on screens. People will be able to play with the simulations; they will be able to change parameters that change the virtual restoration. This software will also help artists with physical restoration work, because they can play with various possibilities."
Universal PDEs
By now you've probably come to appreciate the immense versatility of PDEs. It's this versatility that Markowich exploits in his own work, and that of his research group at Cambridge. He has recently been awarded an eight million dollar grant by a foundation in charge of constructing the new King Abdullah University of Science and Technology (KAUST) in Saudi Arabia. "The foundation gives grants to leading scientists in leading universities in the world to pursue their own interests in their own institutions. The idea is that these scientists bring something back to KAUST. So we will travel to KAUST, speak to people there and help them with recruitment, etc."
"My research group will concentrate on two problems. The first is mathematical modelling in nanotechnology. In PDE terms, this means quantum mechanics. The other is reaction-diffusion and kinetic equations in the biological sciences. It turns out that in mathematical terms, both areas are related. This shows the power of mathematics through abstraction."
So are there any major advances on the horizon? "Mathematics is hard work, and it's done every day on a continuous basis. It's not a strike of genius once every half year. So we're thinking of continuous work and if something big comes out eventually, then we'll be happy."
About this article
Peter Markowich is Professor of Applied Mathematics and Head of the Applied Partial Differential Equations Research Group at the University of Cambridge. You can see more of his images and their connection to mathematics in his talk entitled Applied PDEs: a visual approach, or in his recent book with the same title.
Plus would like to thank Carola-Bibiane Schönlieb, one of Markowich's doctoral students, for her contributions to the section on medieval frescoes.
Marianne Freiberger is Co-Editor of Plus.