
Moss blows smoke rings

The low-growing Sphagnum moss, otherwise known as peat moss. (Image courtesy of Joan Edwards)
What do you if you are only 1cm high and need to get your spores more than 10 cm above the ground so that they are spread by the drifting winds? You blow spore rings.
Peat moss covers 1% of the Earth's land surface and is a vital part of the carbon cycle, potentially storing more carbon than any other type of plant. But this ground-hugging plant needs to get its reproductive spores into the turbulant winds that blow high above it, in order that they spread far and wide.
The spore capsules of the moss are spherical when wet, with the spores sitting in the top of the capsules on a pocket of air. But on sunny days the capsule dries out and shrinks down to a cylinder, about 5/8 of the original volume, squashing the air pocket inside the capsule.

As the spore capsules dry out their shape changes from sphere's to cylinders, until the round cap pops off and the capsule explodes (Image courtesy of Joan Edwards)
Boyle's law says that the number you get when multiplying pressure of a gas by its volume remains constant, and so as the volume of the air pocket in the spore capsule is decreased, the air pressure is increased. In this case the air pressure inside the shrunken capsule is about 400kPa higher than the pressure outside it, about the same as inside a champagne bottle. Eventually the pressure inside the capsule becomes so great, the capsule blows its top and shoots the spores out on a puff of compressed air. The force of the air burst (which is the air pressure times the cross-sectional area of the capsule), accelerates the spores at about 320,000 m/s2.
"The spores are too small to move rapidly through the air," says Professor Joan Edwards, one of the authors of a paper recently published in Science "This feature is a huge advantage to the spores once they achieve height — because this means they can stay 'afloat' in the air and be carried by long distances. But they have to get high first, and this is where the vortex ring is critical."
If the spores were launched individually, like a ball shot out of a cannon, they would quickly decelerate due to air resistance and gravity. An individual spore launched with an initial velocity similar to the that at which the spores leave the capsule (around 13 m/s), they would only reach about 7mm above the ground, way below the 10cm height needed to be picked up by the wind. (You can read more about this sort of trajectory in 101 uses of a quadratic equation: Part II.)
But the sudden release of air and spores through the round capsule opening creates a vortex ring, just like a smoke ring. When the moving ball of air released from the capsule hits the still air outside, the top layer peels around and under, drawing more air in to create a donut shape. Vortex rings often create a mushroom cloud as they draw more air into the centre of the vortex. Indeed the famous mushroom clouds of atomic bombs are created from the vortex ring of fire, smoke and debris produced by the explosion.
"Vortex rings are formed by a sudden symmetrical impulse," says Edwards. "In Sphagnum the capsule builds up 4-5 atmospheres of pressure, so eventually when it literally blows its top, the air rushes out and forms a vortex ring"
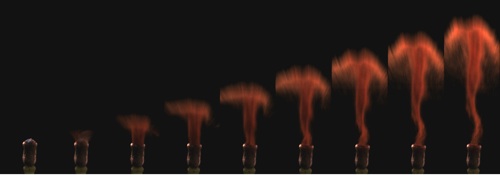
Still frames from a movie of an exploding capsule, the explosion creating a mushroom cloud of spores topped by a vortex ring. (Image courtesy of Clara Hard, Joan Edwards and Dwight Whitaker )
The motion of fluids, such as air, can be described mathematically. One of the solutions of the idealised fluid equations (equations describing the motion of frictionless fluids) is a steadily moving vortex ring. In an ideal fluid, the ring would hold together and carry on moving forever, but in the real world things like friction would gradually slow the vortex ring down and cause it to dissipate. (You can read more about mathematical descriptions of fluid flows in Daniel Bernoulli and the making of the fluid equatio and Understanding turbulence.)
The coherent structure of the vortex ring means that energy is lost more slowly than it would be in a less organised flow, and the vortex ring can travel a long way before breaking up. "Another nice example is that of smoke rings," says Peter Haynes, Professor of Applied Mathematics at the University of Cambridge. "If you blow smoke without succeeding in forming a ring then it doesn't get very far. If you succeed in forming a ring then it propagates a long way."
"The key point is that a vortex ring is a coherent structure (i.e. an organised flow which hangs together) which naturally propagates," says Haynes. "The other important ingredient is that the fluid in the neighbourhood of the vortex ring is carried along with it — in the peat moss case this fluid includes the spores, so the spores can travel long distances." The vortex ring carrying the spores travels much higher than the spores would reach if launched ballistically at similar speeds, reaching heights of up to 20cm.
Jellyfish and squid are known to use vortex rings to propel themselves through water, but this is thought to be the first time plants have been observed producing them. It is thought that blowing spore rings has enabled the ancient moss to compete against other plants who have the added advantage of height.
Comments
Anonymous
Do the spores really accelerate at 320,000 m/s^2
This is much faster than the speed of sound. Also, is s^2--square seconds? If so, this doesn't sound like a speed sort of unit. I would have expected meters per second.
I teach high school science. My AP Environmental Science class just visited a spaghnum bog and your article fits really nicely with our discussion. I'd also like to use this information in a nature column I write, but wanted to check on that speed--isn't that orders of magnitude faster than the speed of sound--is this possible? I have no idea.
Thanks!
Marianne
You are confusing acceleration and speed. Acceleration is measured in metres per second per second.