December 2009
Doubling the cube using origami — proof
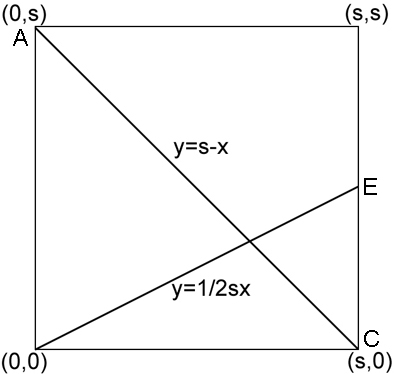 Figure 1
Figure 1
First we show that the first three steps amount to dividing the height of the square into three equal parts. Place the square in a coordinate system with corner  at the point
at the point  . See figure 1. Now the line from
. See figure 1. Now the line from  to
to 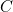 has equation
has equation 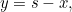 where
where  is the side length of the square. The line from
is the side length of the square. The line from  to
to  has equation
has equation 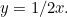 So the two lines meet at a point with
So the two lines meet at a point with  -coordinate satisfying
-coordinate satisfying 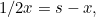 so
so 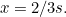 The
The 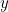 -coordinate of the intersection point is therefore
-coordinate of the intersection point is therefore 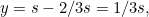 as required.
as required.
The construction claims that the side length 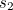 of the new cube is
of the new cube is 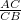 times the side length
times the side length 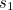 of the given cube. Now since
of the given cube. Now since ![$s_2 = \sqrt[3]{2}s_1$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0004.png) , we have
, we have ![$\sqrt[3]{2}s_1 = \frac{AC}{CB}s_1,$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0005.png) so we need to show that
so we need to show that ![$\frac{AC}{CB}=\sqrt[3]{2}.$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0006.png)
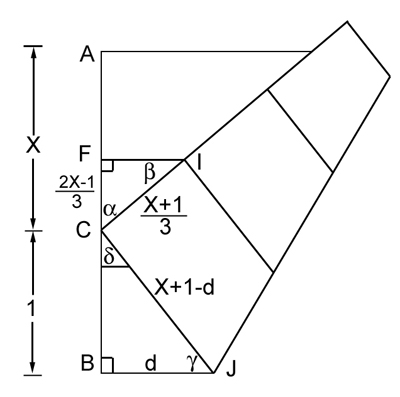 Figure 2
Figure 2
Firstly, we can assume that the length 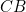 is equal to 1, as we can scale the image as we like without affecting the proportions. We'll write
is equal to 1, as we can scale the image as we like without affecting the proportions. We'll write 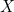 for the length of the line segment
for the length of the line segment 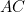 , so the side length of our square is equal to
, so the side length of our square is equal to 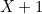 . See figure 2. The line segment
. See figure 2. The line segment 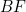 corresponds to two thirds of a side of the square and therefore has length
corresponds to two thirds of a side of the square and therefore has length 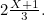 This implies that the length of the line segment
This implies that the length of the line segment 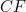 is
is 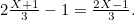 We write
We write 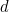 for the length
for the length 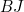 . Since the line segment
. Since the line segment 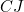 is part of the bottom edge, its length is
is part of the bottom edge, its length is 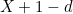 . There is a right angle at
. There is a right angle at  , so by Pythagoras' theorem we have
, so by Pythagoras' theorem we have 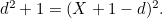 This means that
This means that 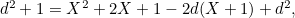 and therefore
and therefore 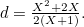 Now consider the two right-angled triangles
Now consider the two right-angled triangles 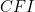 and
and 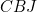 . Considering the 180 degree angle formed at
. Considering the 180 degree angle formed at 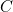 by the vertical edge of the square, we get
by the vertical edge of the square, we get
The angles of the triangle
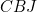
add up to 180 degrees, so
So the triangles
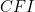
and
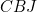
have two equal angles: the right angle and the angle
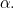
This means that they are
similar. Therefore, the ratios of corresponding sides of the two triagles are equal. Observing that the side
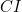
of the triangle
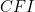
is a third of the side of the square and therefore has length
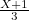
, we get
Substituting the expression for
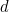
above gives
so
so
This proves the result.
Return to main article

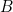 at the point
at the point 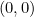 . See figure 1. Now the line from
. See figure 1. Now the line from 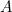 to
to 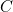 has equation
has equation 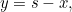 where
where  is the side length of the square. The line from
is the side length of the square. The line from  to
to  has equation
has equation 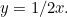 So the two lines meet at a point with
So the two lines meet at a point with  -coordinate satisfying
-coordinate satisfying 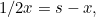 so
so 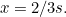 The
The 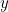 -coordinate of the intersection point is therefore
-coordinate of the intersection point is therefore 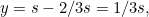 as required.
as required.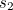 of the new cube is
of the new cube is 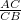 times the side length
times the side length 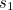 of the given cube. Now since
of the given cube. Now since ![$s_2 = \sqrt[3]{2}s_1$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0004.png) , we have
, we have ![$\sqrt[3]{2}s_1 = \frac{AC}{CB}s_1,$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0005.png) so we need to show that
so we need to show that ![$\frac{AC}{CB}=\sqrt[3]{2}.$](/MI/803a8af8b6f4c73e4a7ee286dfe5abfd/images/img-0006.png)

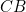 is equal to 1, as we can scale the image as we like without affecting the proportions. We'll write
is equal to 1, as we can scale the image as we like without affecting the proportions. We'll write 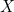 for the length of the line segment
for the length of the line segment 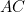 , so the side length of our square is equal to
, so the side length of our square is equal to 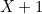 . See figure 2. The line segment
. See figure 2. The line segment 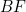 corresponds to two thirds of a side of the square and therefore has length
corresponds to two thirds of a side of the square and therefore has length 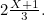 This implies that the length of the line segment
This implies that the length of the line segment 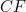 is
is 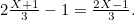 We write
We write 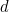 for the length
for the length 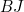 . Since the line segment
. Since the line segment 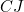 is part of the bottom edge, its length is
is part of the bottom edge, its length is 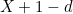 . There is a right angle at
. There is a right angle at 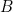 , so by Pythagoras' theorem we have
, so by Pythagoras' theorem we have 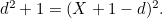 This means that
This means that 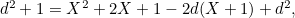 and therefore
and therefore 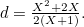 Now consider the two right-angled triangles
Now consider the two right-angled triangles  and
and 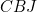 . Considering the 180 degree angle formed at
. Considering the 180 degree angle formed at 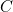 by the vertical edge of the square, we get
by the vertical edge of the square, we get ![\[ \alpha =180-\delta -90 = 90-\delta . \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0020.png)
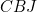 add up to 180 degrees, so
add up to 180 degrees, so ![\[ \gamma = 180 -90 - \delta = 90-\delta = \alpha . \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0021.png)
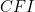 and
and 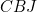 have two equal angles: the right angle and the angle
have two equal angles: the right angle and the angle 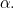 This means that they are similar. Therefore, the ratios of corresponding sides of the two triagles are equal. Observing that the side
This means that they are similar. Therefore, the ratios of corresponding sides of the two triagles are equal. Observing that the side 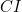 of the triangle
of the triangle 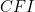 is a third of the side of the square and therefore has length
is a third of the side of the square and therefore has length 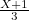 , we get
, we get ![\[ \frac{d}{X+1-d}=\frac{\frac{2X-1}{3}}{\frac{X+1}{3}}=\frac{2X-1}{X+1}. \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0025.png)
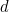 above gives
above gives ![\[ \frac{X^2+2X}{X^2+2X+2}=\frac{2X-1}{X+1}, \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0026.png)
![\[ X^3+3X^2+2X=2X^3+3X^2+2X-2, \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0027.png)
![\[ X^3=2. \]](/MI/e57455168a10bc889dee7a93541b9172/images/img-0028.png)