
Play to win with Nim
Some games are all about luck. Your winning chance depends on the roll of a die or the cards you've been dealt. But there are other games that are only about strategy: if you play cleverly, you're guaranteed to win.
A great example of this is the ancient game of Nim. Whatever the state of the game, there is a winning strategy for one of the two players. And a very cute form of addition tells you which of the two players it is.
The rules of Nim
The traditional game of Nim is played with a number of coins arranged in heaps: the number of coins and heaps is up to you. There are two players. When it's a player's move he or she can take any number of coins from a single heap. They have to take at least one coin, though, and they can't take coins from more than one heap. The winner is the player who makes the last move, so there are no coins left after that move. (Some people play the game the other way around, with the last person to make a move losing the game, but we'll ignore that version for the moment.)
It's clear that there is no luck involved here. You can work out the best move to make by cleverly predicting the sequence of moves that would follow it.
As an example of how the game works, suppose there are three heaps with three, four and five coins respectively. Here is how the game could develop:
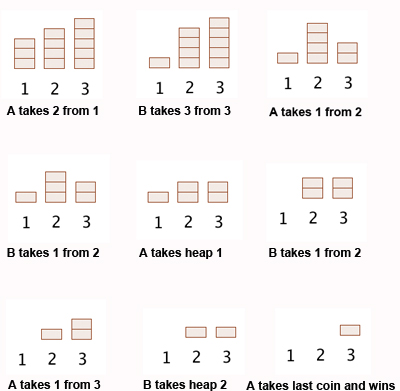
A game of Nim starting with heaps of sizes 3, 4 and 5. Player A wins.
The question we're interested in is this: given a particular configuration of heaps and coins, is there a winning strategy for one of the players? That is; is one of the players guaranteed to win if he or she plays the right moves?
Let's start by playing with some examples. Suppose the two players are called A and B, and suppose that A goes first. Suppose there are two heaps with a coin each. Then clearly, player B is guaranteed to win: A has to take one of the two coins, leaving B to take the last one.
Now suppose that there are two heaps, one of which contains two coins and the other one. Now player A has a winning strategy: take one of the coins in the two-coin heap. This leaves two heaps with a coin each and B to go next. And as we saw in the previous example, this means that A will win.

Who's got the winning strategy?
Let's do one more: suppose that there are two heaps with two coins each. Now player B has a winning strategy. If A takes an entire heap, then B should take the remaining heap and win. If A takes only one coin of one of the heaps, then we are in the same situation as in the previous example, with B to go first. Therefore, B is guaranteed to win if she takes one coin from the two-coin heap.
From this series of examples you can't help but feel that there is some sort of pattern here: that there should be some sort of clever trick that tells you for a given arrangement of coins and heaps whether there is a winning strategy for one of the players. The American mathematician Charles Bouton (1869-1922) felt the same and set himself the daunting task of analysing the game completely. In 1902 he found the trick — and it's subtle! To figure out whether there is a winning strategy and for which player, you first need to...
Go binary
The secret is to write the sizes of the heaps as binary numbers (if you already know how to do this, skip this part.) To see how to do this, let's first remind ourselves of how the ordinary decimal way of writing numbers works. Let's take the number 4302 as an example. The digit 4 in this number doesn't stand for the number 4, rather it stands for 4000, or 4 x 1000. Similarly, 3 doesn't stand for 3 but for 300 = 3 x 100, 0 stands for 0 x 10, and 2 stands for 2 x 1. So 4302 means
4 x 1000 + 3 x 100 + 0 x 10 + 2 x 1.
Similarly, 7396 stands for
7 x 1000 + 3 x 100 + 9 x 10 + 6 x 1.
What do the numbers 1000, 100, 10 and 1, which appear in these expressions, have in common? They are all powers of 10:
1000 = 103
100 = 102
10 = 101
1 = 100.
To write a number in decimal notation, you first write it as a sum of consecutive powers of 10 (with the largest power on the left) and then pull out the coefficients of these powers. We can do the same with powers of 2 rather than 10. For example, the binary number 110 stands for
1 x 22 + 1 x 21 + 0 x 20 = 4 + 2 +0 = 6 (written in decimal).
And the binary number 10001 stands for
1 x 24 + 0 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 16 + 0 + 0 + 0 + 1 = 17 (written in decimal).
You can convince yourself that a binary number only consists of the digits 0 or 1: when you write a number as a sum of consecutive powers of 2, no other coefficients are necessary.
Adding the Nim way

One of the first ever gaming computers, called Nimrod, was designed to play the game of Nim and exhibited at the 1951 Festival of Britain.
The secret to finding the winning strategy hinges on writing the sizes of the heaps (the number of coins in each heap) in binary, and then adding those numbers up — but not using the ordinary way of adding numbers, but something appropriately called Nim addition.
To add some given binary numbers using Nim addition, you first write them underneath each other, as you might for ordinary addition. Then you look at each of the columns in turn. If the number of 1s in a column is odd, you write a 1 underneath it; if it's even, you write a 0 underneath it. Doing this for each column gives a new binary number, and that's the result of the Nim addition.
As an example, let's Nim-add the binary numbers 10, 11, and 100 (which stand for the decimal numbers 2, 3 and 4):
| 1 | 0 | ||
| 1 | 1 | ||
| 1 | 0 | 0 | |
| | |||
| 1 | 0 | 1 | |
So the result, which is called the Nim sum, is the binary number 101. Nim addition is not the same as ordinary addition: the binary number 101 is 5 in decimal, which is not equal to the ordinary sum 2+3+4 = 9.
Who wins?
When Charles Bouton analysed the game of Nim, he figured out two facts which hold the key to the winning strategy.
Fact 1: Suppose it's your turn and the Nim sum of the number of coins in the heaps is equal to 0. Then whatever you do, the Nim sum of the number of coins after your move will not be equal to 0.
Fact 2: Suppose it's your turn and the Nim sum of the number of coins in the heap is not equal to 0. Then there is a move which ensures that the Nim sum of the number of coins in the heaps after your move is equal to 0.
It is not too difficult to prove that these to facts are always true (see for example this article) but you can also convince yourself by playing around with heaps of coins.
Now suppose you are player A, so you go first. Also suppose that the Nim sum of the number of coins in the heaps is not equal to 0. Your strategy will be this: if possible always make a move that reduces the next Nim sum, the Nim sum after your move, to 0. This would then mean that whatever player B does next, by fact 1 the move would turn the next Nim sum into a number that's not 0.
Let's have a go, keeping track of the Nim sums in a table:
| Player to move next | Nim sum | Can this be reduced to 0? | Next Nim sum |
| A | not 0 | Yes | 0 |
| B | 0 | No | not 0 |
| A | not 0 | Yes | 0 |
| B | 0 | No | not 0 |
| A | not 0 | Yes | 0 |
| ... | ... | ... | ... |
This ping-pong between zero and non-zero Nim sums means that you are guaranteed a win! If player B were to win, she would have to make a move that leaves over no coins at all. That is; she would have to make a move that results in a zero Nim sum which, as we can see, is impossible. Your moves, on the other hand, always reduce the Nim sum to zero. And at some point in the game, the zero Nim sum will correspond to there actually being zero coins left — you've won.
This shows that if the Nim sum of coins in the heaps at the start of the game is not 0, then player A has a winning strategy. The strategy is to always make a move that reduces the next Nim sum to 0. (You can check that this is the strategy played by player A in the example at the beginning of this article.)
If the Nim sum of coins in the heaps at the start of the game is equal to 0, then player B has a winning strategy. Whatever player A does on the first move will result in a non-zero Nim sum when it's B's turn. And by the same reasoning as above, this means that the winning strategy is now in B's hands.
Nim addition rules the world

Computers are binary machines.
Nim addition is clearly very useful when you're playing Nim, but that's about it, right? Wrong! It turns out that much of our everyday life depends on this curious way of adding up numbers.
Computers are binary machines. All the information they store, including numbers, is translated in to strings of 0s and 1s. But computers not only store information, they also perform logical operations, based on yes/no answers. For example, given a user name and a password, they need to ask the questions "is the user name correct?" and "is the password correct?" and depending on the answers decide whether or not to let the person entering them log in. Note that this operation takes two inputs (user name correct? password correct?) and returns one output (login yes or login no).
Writing 0 for "no" and 1 for "yes", these logical operations can also be turned into operations involving 0s and 1s. Luckily, it turns out that any logical operation you might ever want to perform can be made out of six basic ones. You simply have to compose them in the correct way.
One of these basic operations is called XOR. It also takes two inputs, each of which can be a 0 or a 1, and returns one output, which can also be a 0 or a 1. Here is the table of outputs XOR returns for a given combination of inputs:
| XOR | ||
| Input | Output | |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
A closer look at this shows that XOR is exactly the same as Nim addition of the digits 0 and 1:
| Nim addition | ||
| Input | Output | |
| 1 | 1 | 1+1 = 0 |
| 1 | 0 | 1+0=1 |
| 0 | 1 | 0+1=1 |
| 0 | 0 | 0+0=0 |
So, many of the operations your computer performs every day are based on Nim addition — without it, things would be very different. You can find out more in the Plus article A bright idea.
About the author
Marianne Freiberger is Editor of Plus.
About this article
This article was inspired by content on our sister site Wild Maths, which encourages students to explore maths beyond the classroom and designed to nurture mathematical creativity. The site is aimed at 7 to 16 year-olds, but open to all. It provides games, investigations, stories and spaces to explore, where discoveries are to be made. Some have starting points, some a big question and others offer you a free space to investigate.
Comments
Anonymous
Marianne,
I enjoyed your article about Nim. Did you know that the game still works if the rule for winning is reversed?
Here is a variation that I use when introducing the game of Nim to a novice. I lay out the piles (usually in the arrangement 2,3,5,7) and explain the rules of play. I then make the bold (and slightly risky statement) that I can always win, whether I move first or you move first and whether the winning player takes the last piece or the losing player takes the last piece. Once the player make those decisions and the game is underway, I get my Nim sum to zero as soon as I can and then play along until a minimum position is reached, such as 3,2,1 or 2,2. Then, I offer to let you reverse the rule about who wins, if you wish. With a little thinking, it's clear that I can win under either rule but my last move must have a Nim sum of one if rule is that the person who takes the last one loses.
It's a great way to introduce a little bit of maths!
If it seems that the person would be overwhelmed by a discussion of binary numbers, I have them visualize each of the piles of markers as being divided into powers of 2. Then you want to play such that after your move each such sub-pile must have a matching partner. For example, with the starting pattern of 2, 3, 5, 7 this becomes 2, 2+1, 4+1, 4+2+1. This is easier for some people than binary numbers.
==Gordon Stallings==
Anonymous
With a 2-3-5-7 configuration, it would seem you have to go first to win. You start the game unbalanced--three groups of 2, two 4's and four 1's. When you go first, you are able to get the Nim sum to zero. After that, assuming the other person knows what she's doing, I don't see how you could win. Every move after your move, the opponent could restore the sum to zero.
A separate Nim question: At the end you are down to 1-1-2. At this point, to get the Nim sum to zero, one must eliminate the row of two it would seem. But that is of course a losing strategy if in order to win, you must not be the one to remove the last coin. Yet, if you employ the winning strategy of leaving the opponent 1-1-1, the Nim sum is no longer zero, which is supposedly what is needed to ensure victory. Any explanation? This is not a logic problem I'm putting out there--I don't know the answer.
Anonymous
If your victory condition is to take the last piece of the board you will always want to follow the strategy of having your move leave the board with a Nim sum of 0. Therefor 1-1-2 --> 1-1 would be the winning move, which is in accordance of the winning strategy.
If however your victory condition is for your opponent to have to make the last possible move, then you have to break the winning strategy in the very end. You will want to stay in control of the board by using the winning strategy up to a point, where you can set up a board in which your opponent's only possible moves leave the board with Nim sum 0 (basically whichever move he could possibly take has to leave the board with a Nim sum of 0). Therefor 1-1-2 --> 1-1-1 is the winning move, as your opponent is forced into a position, where he can not help himself but leave the board with Nim sum 0, which in the end means that he has to pick up the last piece.
Dave Radford
Yes, but you have to be in control at that point to pull it off. If you start with a non-zero Nim sum, and your opponent goes first, provided she doesn't err, you will never be in control.
Walter Holliday
If a person going first always takes out the 3 leaving 2,5,7, your opponent will always lose unless you make a mistake.
Anonymous
If to win, you need to be the one that doesn't take the last counter then the answer is to change 1-1-2 to 1-1-1 so your opponent takes 1, reducing it to 1-1-0, and then you take 1, reducing it to 1-0-0, and your opponent takes the last one, letting you win.
David Hurlburt
There is a simple case where the NimSum= 0 and I can make a move where the NimSum is, again, 0. So the logic is flawed.
Sebastiaan de Jonge
"There is a simple case where the NimSum= 0 and I can make a move where the NimSum is, again, 0."
>> Which case is that?
Anonymous
No such case exists.
sweisser
Fyi, here is an error in the binary notation for 4302 in the first section under "Go Binary." The calculation should read "3 × 100," not "3 x 1000."
Marianne
Thanks for spotting the error, we have fixed it.
Phil
Hello. What is the NIM sum of each row wherein the 1st row contains 3 items the 2nd contains 4 and 3rd contains 5? When calculating the sum, are you calculating horizontal or vertical? Thank you.
Kurt Piersol
This process gets much more fascinating when the victory condition is not known at the start of the game. The game of Whim is identical to Nim, except that one additional class of move is allowed. At any point, once per game, either player can sacrifice his move to set the win condition, which is then permanent. This has the fun side effect of both choosing the win condition and changing the turn order, forcing an additional move by the opposition. I'd be curious to hear your thoughts on Whim. It looks to me like almost identical analysis can get you most of the way to winning Whim, however, the ability to switch turn order and set the win condition means you must pick a suitable time to do that. That's hard to do, because you opponent might beat you to the punch.
aMor
Thanks for posting Whim as a variation on Nim. I will try it out!
W. Aviril Harriman
This is a very interesting Nim variant. I have figured out a strategy for winning. But you have to memorize a few numbers. Well, 23 numbers, to be exact. And here they are:
2 13 45
112 144 155 222 233 247 256 346 357
1113 1145 1223 1246 1257 1333 1347 1356
2245 2344 2355
These numbers assume a layout of 2 3 5 7 = 17 stones. Here's how to win: 1) If your opponent presents you with a balanced board (every power of 2 in each group has its mate in another group), pass your turn and name the object of the game (miserè or standard). It doesn't matter which object you call unless you're very close to the end.
2) If your opponent presents you with an unbalanced board (most of the time), you should take a normal turn and present them with an unbalanced board. The configuration should be one of the 23 numbers above.
If no one calls an object by the time one player presents the other with a single pile of two stones, we have a problem. The active player can simply take the two stones and end the game -- without anyone calling an object! This leaves the outcome in limbo. So I propose that when the game comes down to a single pile of two stones, the active player may simply play according to the normal rules, i.e., take one stone or take both stones or pass their turn and call an object. But if the player chooses to take both stones, their opponent still gets another go. Since there are no more stones left on the table, the opponent's choice is simple: pass and call miserè or pass and call standard. If they call standard, they lose because the other player has already taken the last stones. If they call miserè, they win for the same reason.
I hope you all have fun with this game.
Wyon Stansfeld
another variation on Whim is to add and extra possible win condition - getting the most stones, or plums or peices, whatever you want to call them. I am working on this for a computer program but I have no idea if it works yet
Krenil
What about winner if piles are 2,3,6?
Walter Holliday
If you leave you opponent with 2,3,6 he can’t win unless you make a mistake. The game is much simpler than all this math.
W. Aviril Harriman
She most certainly can win by removing 5 from 6.
Jason
We've played it by having 5 piles and a total of 15 matchsticks. 1st pile has 1 matchstick, 2nd pile has 2 matchsticks and so on. Heap sizes of 1, 2, 3, 4, 5. So it should look like this:
|
||
|||
||||
|||||
Just wondering if there's a method of winning with the same rules as this article has.
Exer
remove a piece from the last pile
W. Aviril Harriman
Begin by removing a single matchstick from row 1 or row 3 or row 5.
Cwr
What would be the NIM solution for a game where taking the last pieces loses and the heaps are 1,3,5,7,9? I’m struggling with the last row because the first four rows are at Nim sum zero which leaves nothing to cancel out the last row of nine.
Hugh Janus
As you say, the first four rows are NIM sum zero, so if you remove the entire row of 9, you are in a winning position
Hugh Janus
If the first 4 rows have NIM sum zero (which you're right, they do) then removing the entire row of 9 leaves the other player with just the 4 zero sum rows.
Ginja
Like you said, there’s only one thing preventing this from having a Nim sum of zero, and it’s that last row of 9. So, remove the row of 9 on your first turn, and now you’ve reached a winning position.