
The powers of the multiplication table
Multiplication tables date back to Babylonians from over 4000 years ago. The earliest decimal examples appeared in China in around 300BC, constructed using bamboo strips, and could be used to multiply whole and half integers up to 99.5. One of the earliest examples we'd recognise is the Table of Pythagoras included by Nichomachus in his Introduction to Arithmetic from around 100AD.

One of the earliest examples of a decimal multiplication table, constructed using bamboo strips, from around 300BC in China
Today, at school the times table is a device students use to learn multiplication through rote rehearsal and rapid-fire memory drills. Although some view mastery of the times table as an achievement in itself, really it gives students a sturdy foundation to lay mathematical brick. Let's take a dip in deeper waters and explore some amazing patterns that reveal the powers hidden in the multiplication table.
Triangles and squares
In a sea of integers, the red numbers on the main (Northwest to Southeast) diagonal of the multiplication table are clearly square numbers – the counting numbers raised to the power of 2.
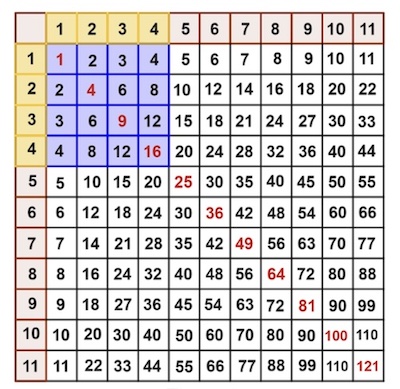
In the Plus article Triangular number patterns, the authors unveiled that the multiplication table also gives us triangular numbers (numbers that can be represented by a pattern of dots arranged into an equilateral triangle). Summing up the numbers in each square lattice starting in row 1 and column 1, gives us the triangular numbers squared.
Summing up the numbers in the square lattices starting in row 1 and column 1 give us the triangular numbers squared.
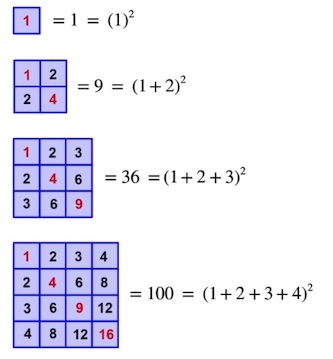
Not only can triangular numbers be unearthed in the multiplication table, it can give us square numbers as well. We saw in the same Plus article that when multiples of a number $k$ are coloured blue (see below), the sum of the numbers in a square lattice enclosed by these blue multiples also involves a triangular number. The sum of the numbers in the square lattice is equal to $(2m-1)(2n-1)T_{k-1}^2$, where $m$ and $n$ identify the square lattice by counting from the top and left respectively, and $T_{k-1}$ is the $k-1^{st}$ triangular number.
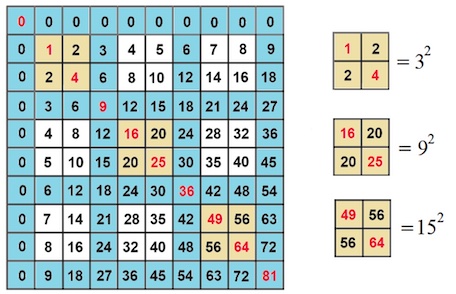
We can see that the sums of the square lattices enclosed by the blue multiples on the main (Northwest to Southeast) diagonal (coloured in yellow below) are also square numbers. This can easily be proven by taking the original sum formula from the article and modifying it. We will only use $m$ in the formula because the vertical and horizontal positions are the same. $$ (2m-1)(2m-1)T_{k-1}^2 = ((2m-1)T_{k-1})^2. $$
Splitting squares
If we wade into other square lattice formations of different size and geography in the times table, we can find more square numbers. A square lattice that hinges on the main (Northwest to Southeast) diagonal always seems to generate a corresponding square number based on the sum of the shared column and row labels. The sum of the square lattice consisting of the single square from row 2, column 2 is $2^2=4$. The numbers in the square lattice at the intersection of rows and columns 3 and 4 add together to give $(3+4)^2=49$, and the sum of the numbers at the intersection of rows and columns 5, 6 and 7 is $(5+6+7)^2= 324$.
The multiplication table, with the labels for the rows written down the left side, and the labels for the columns written across the top.
This even seems to hold when a square lattice is constructed by intersecting non-consecutive rows and columns. If we take the intersection of the rows and columns 1, 4 and 8 , the sum of the (split) square lattice is $(1+4+8)^2 = 169$.
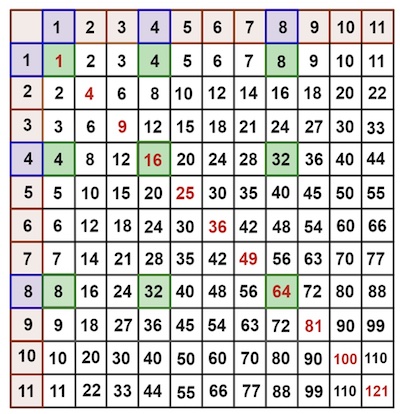
There's some mathematical insight as to why this works with three integers $a$, $b$ and $c$ chosen from the multiplication table to define the lattice, and we can come up with a general formula that works for any three numbers. In our example above the sum of the numbers in the square lattice is: $$ \begin{array}{rl} & 1\times 1+1\times 4+1\times 8 + 4\times 1+4\times 4+4\times 8 + 8\times 1+8\times 4+8\times 8 \\ = & 1(1+4+8) + 4(1+4+8) + 8(1+4+8) \\ = & (1+4+8)(1+4+8) \\ = & (1+4+8)^2. \end{array} $$ And more generally $$ a(a+b+c) + b(a+b+c) + c(a+b+c) = (a+b+c)^2. $$ The sum of the numbers in the square lattice created by intersecting the same set of rows ($a$, $b$ and $c$) with the matching set of columns ($a$, $b$ and $c$), gives you the square of the sum of the row/column labels $(a+b+c)^2$. Can this extend to four numbers, five numbers, and beyond?
Squares of squares and squares of cubes
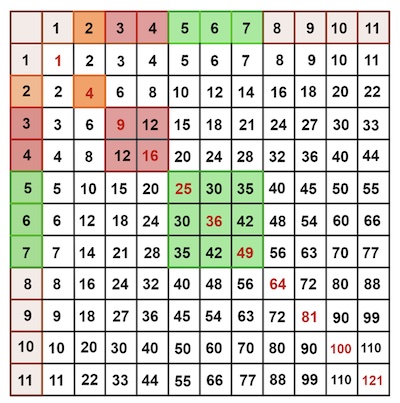
Because of this knowledge we can unearth some extraordinary patterns. For example, you can quickly show (perhaps with some lego!) that the sum of consecutive odd numbers (starting from 1) equals a square. Let's look at intersecting rows labeled with consecutive odd numbers with the matching columns.
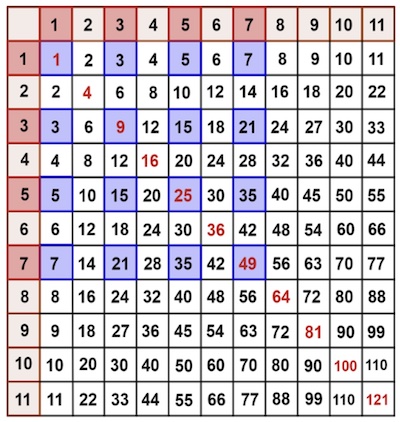
The sum of the row/column labels will be a square number, as this is the sum of consecutive odd numbers which we know is a square. And the square of the sum of the row/column labels will be a square of a square number: that is a number raised to the fourth power. So we can harvest positive integers that are raised to the 4th power from the multiplication table using this particular lattice formation.
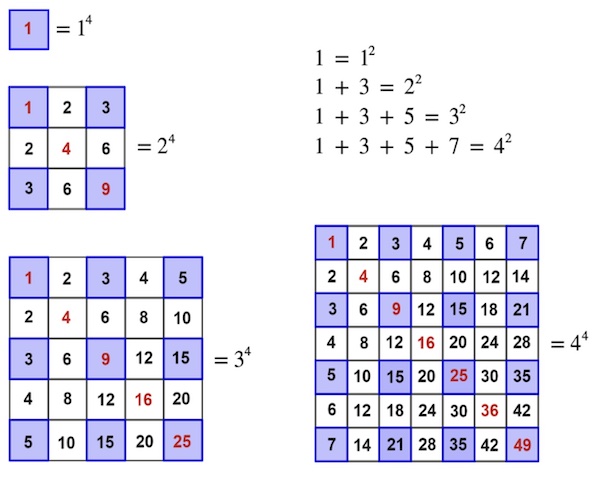
The sums of the blue squares in the intersection of the consecutively odd numbered rows and columns gives you numbers that are raised to the 4th power.
We can use another interesting result, that a cubic number (a number raised to the power of 3) can be written as a sum of consecutive odd numbers. For example, $1^3=1$, $2^3=8=3+5$ and $3^3=27=7+9+11$. So if we choose square lattices that are the intersection of these consecutive odd numbered rows and columns, the sum of the numbers in those square lattices will be the square of a cubic number, that is a number raised to the power of 6. The green squares below are the intersection of rows and columns 3 and 5, and their sum is $(3+5)^2=(2^3)^2=2^6$. And the yellow squares are the intersections of rows and columns 7, 9 and 11, so their sum is $(7+9+11)^2=(3^3)^2=3^6$.
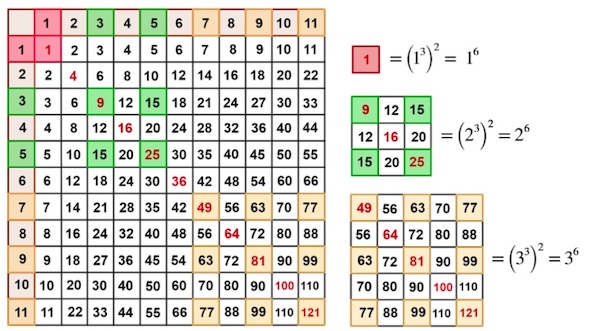
Mathematics teachers are always looking for novel ways to introduce the concepts of multiplication, exponents, and algebra. If we think outside of the box, we find that the multiplication table is more than just a device to memorise your times tables. If we choose to dive deep into the crystal blue waters, we will discover many mathematical treasures in her seabed.
Further reading
Read more on Plus about triangular numbers and where you can find them in the multiplication table.
About the article

Tony Foster is Executive Director and GED Math instructor for Amarillo Area Mental Health Consumers and helps people with mental illness find purpose in life. He is also an amateur mathematician, and his interests include Pascal's Triangle, infinite series, and combinatorics. His findings have been published in Mathematics Teacher journal, the Mathematical Gazette, and Interactive Mathematics Miscellany and Puzzles.

Sai Venkatesh is a Mathematics enthusiast and a passionate teacher. He teaches middle school and senior school students at Step By Step School, Noida, India. He believes in students enjoying Mathematics just like they enjoy any art form.