Maths in a minute: Triangular numbers

A triangular number is a number that can be represented by a pattern of dots arranged in an equilateral triangle with the same number of dots on each side.

For example:

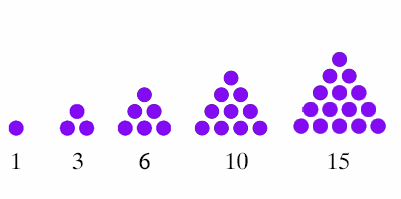
The first triangular number is 1, the second is 3, the third is 6, the fourth 10, the fifth 15, and so on.

You can see that each triangle comes from the one before by adding a row of dots on the bottom which has one more dot than the previous bottom row. This means that the $nth$ triangular number $T_ n$ is equal to

$T_ n=1+2+ 3+...+n.$

There’s also another way we can calculate the $nth$ triangular number. Take two copies of the dot pattern representing the $nth$ triangular number and arrange them so that they form a rectangular dot pattern.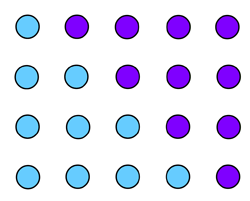

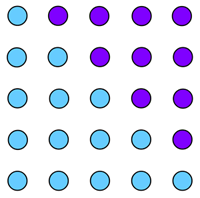
This rectangular pattern will have $n$ dots on the shorter side and $n+1$ dots on the longer side, which means that the rectangular pattern contains $n(n+1)$ dots in total. And since the original triangular dot pattern constitutes exactly half of the rectangular pattern, we know that the $nth$ triangular number $T_ n$ is

$T_ n=\frac{n(n+1)}{2}.$

Note that with this consideration we have proved the formula for the summation of $n$ natural numbers, namely

$1+2+ 3+...+n=\frac{n(n+1)}{2}.$

Triangular numbers have lots of interesting properties. For example, the sum of consecutive triangular numbers is a square number. You can see this by arranging the triangular dot patterns representing the $nth$ and $(n+1)st$ triangular numbers to form a square which has $n+1$ dots to a side:

Alternatively, you can see this using the formulas for the consecutive triangular numbers $T_ n$ and $T_{n+1}$ :

$T_ n+T_{n+1} =\frac{n(n+1)}{2}+\frac{(n+1)(n+2)}{2}=\frac{(n+1)(2n+2)}{2}=(n+1)^2.$

What is more, alternating triangular numbers (1, 6, 15, ...) are also hexagonal numbers (numbers formed from a hexagonal dot pattern) and every even perfect number is a triangular number.

Triangular numbers also come up in real life. For example, a network of $n$ computers in which every computer is connected to every other computer requires $T_{n-1}$ connections. And if in sports you are playing a round robin tournament, in which each team plays each other team exactly once, then the number of matches you need for $n$ teams is $T_{n-1}.$ These two results are equivalent to the handshake problem we have explored on Plus before.

We would like to thank Zoheir Barka who sent us the first draft of this article. We will publish a lovely article by Barka about triangular numbers soon. In the mean time, you can read Barka's article about beautiful patterns in multiplication tables here.