Schrödinger's equation — in action

In the previous article we introduced Schrödinger's equation and its solution, the wave function, which contains all the information there is to know about a quantum system. Now it's time to see the equation in action, using a very simple physical system as an example. We'll also look at another weird phenomenon called quantum tunneling. (If you'd like to skip the maths you can go straight to the third article in this series which explores the interpretation of the wave function.)

The particle in a box.

Suppose you have a particle bouncing back and forth between two walls in a box. Assume that the particle moves in one dimension only, along the $x$-axis, between vertical, impenetrable walls at $x=0$ and $x=L.$ There are no forces acting on the particle inside the box, so its potential energy is zero here: $V(x,t)=0$ for $0L$) because it would need an infinite amount of energy to get there. This means that $\psi=0$ for $x0$ and $x>L.$ And since $\psi$ is continuous at the boundary of the box, we deduce that $\psi$ is also equal to zero at $x=0$ and $x=L.$ The first condition, $\psi = 0$ at $x=0$, means that $$0 = A \cos{0} + B \sin{0} = A,$$ so we can ignore the cosine term in (2) and our equation becomes \begin{equation}\psi = B \sin{\left(\sqrt{\frac{8 \pi^2 mE}{h^2} }x\right)}\end{equation} The second condition, $\psi=0$ at $x=L$, means that $$0=B \sin{\left(\sqrt{\frac{8 \pi^2 mE}{h^2}} L\right)},$$ so either $B=0$ or the sine term is zero. The former would imply that $\psi$ is zero everywhere — this clearly can't be the case as we know that the particle is somewhere in the box. So we deduce that $$\sin{\left(\sqrt{\frac{8 \pi^2 mE}{h^2}} L\right)} =0.$$ Now $\sin{y}=0$ if and only if $y$ is a multiple of $\pi$, so we have $$\sqrt{\frac{8 \pi^2 mE}{h^2}} L = 0, \pi, 2 \pi, 3\pi, ...$$ In other words $$\sqrt{\frac{8 \pi^2 mE}{h^2}} L = n\pi$$ for $n$ a positive integer. This tells us that the energy of the particle can only have discrete values \begin{equation}E_n = \frac{n^2 h^2}{8mL^2},\end{equation} for $n=0, 1,2,3,...$ The number $n$ corresponding to the energy level $E_n$ is called the quantum number of $E_n$. The quantum number $n=0$ corresponds to zero energy — but it also gives a wave function $\psi_0$ which is zero everywhere in the box, which would mean the particle cannot be anywhere in the box. Thus, the quantum number $n=0$ is also ruled out, so the permissible energy levels are \begin{equation}E_n = \frac{n^2 h^2}{8mL^2},\end{equation} for $n=1,2,3,...$

Wave-particle duality is a central concept in quantum mechanics.

The fact that the energy spectrum is discrete, ie that not all energies are permitted, and in particular that zero energy is not permitted, are results you don't get out of classical mechanics — in fact, they fly in the face of conventional wisdom, which holds that quantities such as energy should vary continuously: "nature does not make jumps" according to Gottfried Leibniz. Classical physics also tells us that the lowest energy state of a system (also called the ground state or the vacuum) should have zero energy. But these strange quantum results tally with the experimental observations of quantum systems, for example the discrete energy spectrum of the hydrogen atom.

The value of the constant B can be found by normalising the wave function. Recall that $$|\Psi(x)|^2 = |\psi(x)^2 e^{-(2 \pi i E/h)t}| = |\psi(x)^2||e^{-(2 \pi i E/h)t}|.$$

Now $e^{-(2 \pi i E/h)t}$ is a complex number, which can also be written as $$e^{-(2 \pi i E/h)t} = \cos{\left( -(2 \pi i E/h)t\right)} + i \sin{\left( -(2 \pi i E/h)t\right)}.$$ The modulus $|e^{-(2 \pi i E/h)t}|$ of this complex number is therefore $$\cos^2{\left( -(2 \pi i E/h)t\right)} + \sin^2{\left( -(2 \pi i E/h)t\right)}=1,$$ by the familiar trigonometric identity. Therefore we have $$|\Psi(x)|^2 = |\psi(x)^2 e^{-(2 \pi i E/h)t}| = |\psi(x)^2||e^{-(2 \pi i E/h)t}| = |\psi(x)^2|.$$ Now recall that $|\Psi(x)|^2$ is the probability density function for finding the particle at location $x$ at time $t.$ In other words, the probability that the particle is somewhere in the box is given by $$\int^L_0 |\Psi(x)|^2dx = \int^L_0 |\psi(x)|^2 dx.$$ Since we know for sure that the particle is somewhere in the box we have $$\int^L_0 |\Psi(x)|^2dx = \int^L_0 |\psi(x)|^2 dx = 1. $$ Substituting our expression for $\psi(x)$ from equation (3) we have $$\int^L_0{B^2 \sin^2{\left(\sqrt{\frac{8 \pi^2 mE}{h^2} }x\right)}dx}=1.$$ Using the fact that $$\int \sin^2{(ax)} dx = -\frac{1}{2a}\sin{(ax)}\cos{(ax)}+\frac{x}{2},$$ we can work out that $$B=\sqrt{\frac{2}{L.}}$$

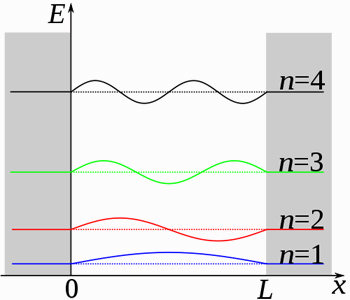
The particle in a box: the position of the particle is shown on the x-axis and the energy on the y-axis. The permitted energy levels for the first four quantum numbers are shown as horizontal dotted lines. The wavefunctions are shown superimposed on the diagram at the corresponding energies. Image: Papa November.

Now $$\psi(x) = \sqrt{\frac{2}{L}} \sin{\left(\sqrt{\frac{8 \pi^2 mE}{h^2}} x\right).}}$$ Substituting the possible values $E_n$ for $E$ from (4) we get infinitely many wave functions $\psi_n(x)$ (one for each quantum number, ie permitted energy level): $$\psi_n(x) = \sqrt{\frac{2}{L}}\sin{\left(\frac{n\pi x}{L}\right)$$ for $0 x L$ and $$\psi_n(x) = 0$$ elsewhere. This gives us another surprising result: for any value of $n$ that is bigger than 1 we can find a value of $x$ that lies within the box for which $|\psi(x)|^2 = 0:$ if $x = \frac{kL}{n}$ for some integer $k n$, then $0
Since $|\psi(x)|^2=|\Psi(x)|^2$ is the probability density of finding the particle at the point $x$, this means that there are places in the box where the particle can never be found! Thus we've seen how Schrödinger's equation produces some very weird results that contradict our classical intuition. So why do we not see things like the discrete energy levels in macroscopic objects like billiard balls? The lowest permitted energy occurs for the quantum number $n=1$ and $$E_1 = \frac{h^2}{8mL^2}.$$ Planck's constant $h$ is very small, $h=6.626068 \times 10^{-34} m^2kg/s.$ So for a large object, $m$ and $L$ will be comparatively huge. This means that $E_1$ will be so incredibly small that an object with energy $E_1$ becomes indistinguishable from one at rest. This is why in the macroscopic world a zero energy level does appear to be possible. Now let's compute the difference between two adjacent energy levels $E_n$ and $E_{n+1}$ for a quantum number $n$: $$E_{n+1}-E_n = \frac{(n+1)^2 h^2}{8mL^2} - \frac{n^2 h^2}{8mL^2} = \frac{h^2((n+1)^2-n^2)}{8mL^2} = \frac{h^2(2n+1)}{8mL^2}.$$ As the mass $m$ and the size $L$ of the box get large, this difference tends to zero. So for large objects the permitted energy levels are so close together that it's impossible to distinguish them from the energy levels that are not permitted — the energy level appears to vary continuously.

Quantum tunneling

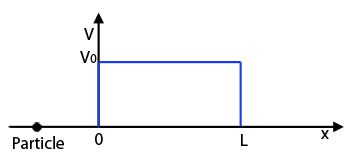
Quantum tunneling: The vertical axis shows the potential energy of the particle, which is equal to V₀ for x greater than 0 and less than L and zero elsewhere.

Now let's change our set-up a little. Let's still assume that our particle moves along the $x$-axis. But this time suppose that the potential energy $V$ is zero for $-\infty x \leq 0$ and for $L \leq x +\infty$ but non-zero between $0$ and $L$. So $V=V_0\neq 0$ for $0 x L.$ This is a potential barrier: classical physics tells us that if the particle is moving right along the negative $x$-axis towards 0, it can only penetrate the region between $0$ and $L$ if its energy $E$ is greater than $V_0.$ It's a bit like a ball of mass $m$ rolling along and encountering a hill of height $H$: if it has enough energy to move to the top of the hill, then its potential energy there will be $V_0 = mgH,$ where $g$ is acceleration due to gravity. If its energy is less than $V_0$ the ball will never make it to the top. Only in our example the hill has a vertical slope because the potential energy jumps discontinuously between 0 and $V_0$ at $x=0$ and $x=L$, and it is flat on the top because the potential energy is constant for $0 x L.$ It turns out that in quantum mechanics the particle can make it to the top, and even the other side, of the "potential hill" even if its energy is less than $V_0$. We won't go into the details here but solving Schrödinger's equation (assuming $E

Generally the term quantum tunneling refers to any situation in which a particle overcomes a potential barrier that it should not be able to overcome according to classical physics. Quantum tunneling does occur in nature, for example in when uranium decays to thorium in a form of radioactive decay known as alpha decay. Here the atomic nucleus emits an alpha particle (which consists of two protons and two neutrons and is structurally identical to a helium nucleus). According to classical physics, the process of emitting the particle should be impossible, as it requires more energy than the atom has available. It's through quantum tunneling that the atom accomplishes the feat.

The big question raised by all this mathematics is what Schrödinger's equation tells us about physical reality. How should we interpret its solution, the wave function? This is what we'll explore in the third article.

Read the final article Schrödinger's equation, what does it mean?

About the author

Marianne Freiberger is Editor of Plus. She would like to thank Jeremy Butterfield, a philosopher of physics, Nazim Bouatta, a Postdoctoral Fellow in Foundations of Physics, and Tony Short, a Royal Society Research Fellow in Foundations of Quantum Physics, all at the University of Cambridge, for their help in writing these articles.

Comments

Wonderful site and content

Marianne,

This is a wonderful site and content. All students of math and physics should read this kind of material.

Many thanks! Keep up the good work!!

Raj

Schrödinger's equation, what does it mean?

Finally an article meant to teach.....Thank You Marianne Freiberger
Too many articles just go through the derivation of Schrodinger's Equation.

Jack H

Planck's constant

Question for Marianne:

Is it possible that h/2 is the fundamental quantum size? If we define a new Planck's constant (call it hs) such that hs = h/2, and plug that into the Schroedinger Equation, does that change the usefulness of the equation (or add any other complications to any aspect of physical laws or quantum mechanics)?

I have a reason for asking that, which we can discuss if your answer is no.

Planck's constant

Interesting thought, perhaps even 1/4 ? I am interested in discussing this.

Question about equation 5

Thx for a very fine article. Very clever math! But I've been stumped by magicians who were as clever. The particle must know the location of L before he/she/it can leave x=0, or he/she/or it will not know when to pop back into reality. How does he/she/or it manage that? What was Schrodenger smoking? :>)

Thomas