
Schrödinger's equation — what does it mean?
In the first article of this series we introduced Schrödinger's equation and in the second we saw it in action using a simple example. But how should we interpret its solution, the wave function? What does it tell us about the physical world? We went to speak to Tony Short and Nazim Bouatta, both theoretical physicists at the University of Cambridge, to find out.

This picture was taken at the 5th Solvay conference in 1927. Wolfgang Pauli is fifth from the left in the back row, Werner Heisenberg 6th from the left in the back row, Louis de Broglie is 7th from the left in the middle row, Max born 8th from the left in the middle row, Niels Bohr 9th from the left in the middle row, Max Planck is second from the left in the front row and Albert Einstein is fifth from the left in the front row.
Schrödinger's equation is to quantum mechanics what Newton's second law of motion is to classical mechanics: it describes how a physical system, say a bunch of particles subject to certain forces, will change over time. In classical mechanics what you're after are the positions and momenta of all particles at every time $t$: that gives you a full description of the system. In quantum mechanics the information about the system is contained in the solution to Schrödinger's equation, a wave function $\Psi.$ The square of the absolute value of the wave function, $|\Psi|^2,$ is interpreted as a probability density. For example, with our particle in a box $|\Psi(x)|^2$ gives the probability density for finding the particle at position $x.$ But it is also possible to solve Schrödinger's equation for many particle systems and to find wave functions for other observable quantities, for example the momenta of the particles.
Where are all the waves?
So what, exactly, does quantum mechanics tell us about physical reality? Schrödinger's equation grew out of the idea that particles such as electrons behave like particles in some situations and like waves in others: that's the so-called wave-particle duality (see the first article of this series). One question that comes up immediately is why we never see big objects like tables, chairs, or ourselves behave like waves.
As a heuristic argument, recall de Broglie's relationship between the wavelength $\lambda$ and the momentum $p$ of a "matter wave": $$\lambda=h/p,$$ where $h$ is Planck's constant. (Again see the first article of this series.) The momentum $p$ of an object is its mass times its velocity. One consequence of quantum mechanics is that no object is ever completely at rest, so $p$ will never be zero. But Planck's constant $h$ is so incredibly small, $h=6.626068 \times 10^{-34} m^2 kg/s,$ that even the tiniest bit of mass and velocity make the wavelength $\lambda$ vanishingly small as well. So small that we usually don't perceive the waviness of macroscopic objects. (We say "usually" here because this general argument does not always apply: there are situations in which quantum effects do become perceptible at a macroscopic scale.)
A wave is not a wave
The next question is how to interpret the wave function. Unlike a classical description of a physical system, the wave function does not give us definite information about the location of a particle at a given time t — it only gives us the probability of finding the particle in a given location at time t. We normally use probabilities to quantify our ignorance: if I say a coin has a fifty-fifty chance of coming up heads or tails, then this simply reflects the fact that I don't yet know how it will come up after the next throw. So perhaps the probabilities given by the wave function measure our ignorance in a similar way: as the particle is moving around in a box, say, it's somewhere definite all the time, only we just can't tell where until we make a measurement. De Broglie did indeed pioneer such a deterministic approach. It was later developed by David Bohm and has become known as the pilotwave or causal interpretation of quantum mechanics, or as Bohmian mechanics. But it's a minority view. Most physicists believe that experiments like the double slit experiment suggest that a particle really can become delocalised in space. "There is a sense in which the particle is in all these different places at once, but the worry about saying this is that there still is only one particle," says Short.
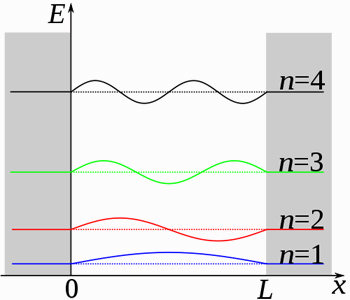
The particle in a box: the position of the particle is shown on the x-axis and the energy on the y-axis. The permitted energy levels for the first four quantum numbers are shown as horizontal dotted lines. The wavefunctions are shown superimposed on the diagram at the corresponding energies. Image: Papa November.
So perhaps the wave function describes a physical wave in space along which the particle is spread out like goo — we never see this particle goo because somehow it contracts to one point when we make a measurement. That's an idea to banish from your head straight away! In our particle in a box example, the solutions to Schrödinger's equation, $$\psi_n(x) = \sqrt{\frac{2}{L}} \sin{\left(\sqrt{\frac{npx}{L}}\right),}$$ for $n = 1,2,3,4, ..$ do indeed describe waves along which the particle "goo" might conceivably be spread out. But this picture collapses once you have several particles. Suppose, for example, there are three of them. In this case the wave function is a function of many variables (three coordinates for the possible positions of each of the three particles and time) and in general it is not possible to break it up into components corresponding to each particle. Now you can't even plot this "wave" because you'd need more than three dimensions to do it. In general the wave function doesn't describe a physical wave because it isn't a function defined on physical space. Rather, it's defined on configuration space: it takes as input all the possible configurations of locations the particles could be in and it returns a value related to the probability that you will find the particles in the given configuration at the given time.
The fact that you cannot always neatly separate the wave function of a many-particle system into individual components illustrates another weirdness of quantum mechanics: that two particles that have once interacted, so that the system they form is described by a single wave function, can remain mysteriously linked even when they have moved light years apart. This mysterious connection is called quantum entanglement. When something happens to one of the entangled particles, a corresponding thing happens to its distant partner, a phenomenon Einstein described as "spooky action at a distance".
But while the wave function generally doesn't represent a straightforward wave in three-dimensional space, the question remains whether there is some sort of physical wave associated to it. Several physicists, including de Broglie, Schrödinger and Bohm, believed that there should be, but although their efforts to find one still continue today, they have not resulted in theories that enjoy mainstream approval.
Others, including Wolfgang Pauli, Werner Heisenberg and Niels Bohr were against this realistic picture and regarded the wave function as a mere mathematical tool to provide probabilities. Indeed, they argued that questions such as "where is the particle when we are not looking" are meaningless: science cannot describe nature per se, but only our knowledge of it. So the only kind of questions we can answer are questions about possible outcomes of measurements. And that's precisely what the wave function gives us. This view is known as the Copenhagen interpretation of quantum mechanics. It's in stark contrast to the intuition classical physics is based on: that there exists an objective reality even when we're not looking and that science can describe that reality.
The measurement miracle
Whether there's a physical wave or not, the big question that remains is what happens when we come along and make a measurement. We will only ever find the particle in one spot, yet Schrödinger's equation tells us nothing about why this should be the case, or where that spot should be. Its solution only gives us probabilities. And there is another aspect of the equation which illustrates this tension with reality even more forcefully: it's a linear equation. This means that if some wave function $\Psi_1$ is a solution and some other wave function $\Psi_2$ is also a solution, then the sum $\Psi= \Psi_1 + \Psi_2 $ is a solution too. But $\Psi_1$ and $\Psi_2 $ could correspond to vastly different situations, for example $\Psi_1$ might correspond to the particle being on the Moon (so it's zero for all locations that are not on the Moon) and $\Psi_2$ might correspond to the particle being on Earth (so it's zero everywhere apart from on Earth). Since the sum $\Psi_1 + \Psi_2$ is also a solution, there is a sense in which the particle is in both places at once. When this happens we say that the particle is in superposition of the two states $\Psi_1$ and $\Psi_2$.
"When we do an experiment we don't see all these superimposed solutions, we see only one of them," says Bouatta. "This is in tension with the equation. When you look only to the equation you don't understand what happens at the measurement." There is no consensus among physicists as to how this measurement miracle comes about. "Most people probably don't commit to an interpretation, they just say we're not sure," says Short. But there are several schools of thought that try and provide an answer.
Collapsing waves
One of them asserts that when a measurement is made, the particle somehow "decides" where it is going to be. The corresponding wave function then simply collapses. In our particle in a box example, the wave function was non-zero at many places in the box, reflecting the fact that there's a non-zero probability of finding the particle at these places. Once we have opened the box and found the particle in a definite location, it's definitely nowhere else, so the wave function now has a single non-zero value at that location and is zero everywhere else — if you plot it, which you can in this simple example, it will have a single spike at the non-zero location. When we make a measurement an instant later, the particle is very likely still in the immediate vicinity, so the wave function spreads out a bit, but still has a single peak. Over time it will spread out more and more.
One problem with the collapse approach is how distant parts of the wave function "know" that a measurement has been made and thus that they are supposed to collapse. For example, suppose a particle is in superposition between two locations, as described above, and that one of these locations is on the Earth and the other on the Moon. If an observer on Earth now detects the particle, the Moon wave function has to vanish instantaneously. But Einstein's theory of relativity says that no message and no signal can travel faster than light.

Sir Roger Penrose is one of the scientists who have toyed with the idea that consciousness might be necessary to collapse the wave function. Image: Festival de la Scienza.
The collapse idea also raises another question: what is a measurement? Some physicists, including Eugene Wigner and Roger Penrose, have toyed with the idea that a measurement requires an observer and that it is the consciousness of the observer that causes the collapse (which then begs the question of whether a snail, say, has enough consciousness to collapse a wave function). But this approach has largely fallen out of favour. Instead, a measurement is defined as an interaction between the system you're measuring and the measuring device. "For example, an interaction could be: if the particle is on the right, move the pointer on my device to the right and if it's on the left, move the pointer to the left," says Short. "You can model this easily in normal quantum theory."
The challenge for advocates of the collapse approach is to come up with models that describe the workings of the collapse — how exactly does it happen and what causes it? There's a minority view that help may come from the one force that physicists haven't yet been able to reconcile with quantum mechanics: gravity. Finding a unified theory of quantum gravity is the holy grail of modern physics and some people believe that it might shed light on the collapsing behaviour. But this is a highly speculative approach.
Many worlds
As it stands, the idea that the wave function collapses after a measurement needs to be postulated as an extra rule of quantum mechanics. Pulling a new law of nature out of a hat like that isn't a very satisfactory solution for purists — but there is another approach: perhaps all the possible outcomes of a measurement are equally real. "The idea is that there are different worlds that are all real and in each of them the particle is in a different position," explains Short. The problem then becomes how to interpret the probabilities given by the wave function. "You can regard it as a kind of weight you ascribe to each world. If you pick a world at random you're most likely to pick [one with a bigger probability]."
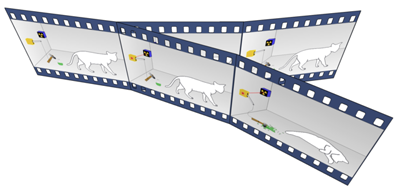
Schrödinger devised a famous thought experiment in which a cat in a box is in superposition of two states: dead and alive. But when you open the box to observe the cat you only ever find it in one of these states. According to the Everett interpretation, when you make the observation the world splits into two branches: in one of them the cat is dead and in the other alive. Image: Dc987.
This is already pretty weird when you're only thinking of tiny little particles. But what about us, the observers? If you include them in this many worlds view, you get the so-called Everett interpretation of quantum mechanics (named after the physicist Hugh Everett). "Suppose you have a little microscopic particle that could be here or there, and then I look at it," says Short. "A collapse model would say that this really decides the issue, the particle makes up its mind and I see it over here or I see it over there, but there still is only one truth to what I see. But macroscopic objects are made up of particles, so there is no reason to believe they should obey different laws of physics. And if you apply [to me, as an observer,] the same laws of physics that you apply to microscopic objects, what you find is that you get this superposition of 'the particle is here and I saw it here' and 'the particle is there and I saw it there'. The Everett interpretation says, well maybe this is what happens. It seems pretty crazy because there are then two copies of me seeing different things. But each of these people, if you ask them if they saw something reasonable, will say yes."
The obvious question now is why we're never aware of these other copies of ourselves. But there's a straightforward answer. Two separate worlds could only interfere with each other if their wave functions were non-zero in the same region in configuration space — that's the possibility space containing all the different configurations of the particles that make up you, the particle you're observing, the measuring device, and so on. But this means that the two copies of you must have identical memories. "In order for two [copies of you] to get mapped into the same state in configuration space, you essentially have to unwind everything in their brain," says Short. "If they have any memory then they're not going to the same place in configuration space because that memory is part of them. If their brain is different, then they can't meet." So only complete amnesia would enable you to meet and merge with yourself. If you're suffering from that, you probably wouldn't notice the merger; and even if you did nobody would believe your incoherent ramblings anyway.
The Everett interpretation may lose out on common sense appeal, but you can argue that it gains in terms of mathematical simplicity. "People say that it seems completely unreasonable, parallel worlds and all this craziness, but actually it's very simple: all you do is take Schrödinger's equation and keep it all the way up to the macroscopic level. Everett simply drops the second law [which postulates the collapse of the wave function] completely," says Short. And Bouatta suggests that we shouldn't push our common sense perception of the world too far. "We have an intuition of our every day life — chairs, tables, birds, etc — and we try to apply this to all different regimes in the Universe: the largest scale but also the smallest scale. But why should the world at every scale be described by our common sense, everyday-life intuition? The consequences of Everett may seem a bit strange, but one may argue that this is the most conservative approach to quantum mechanics because you don't have to [introduce new] laws."
Collapse models and the Everett view are among the most prominent interpretations of quantum mechanics, but there are others too. The truth is that we simply don't know yet what really goes on in the physical world and how to interpret the mathematical formalism that describes it so well. What seems certain is that we have to radically expand our view of the world, but this wouldn't be the first time: who would have believed a thousand years ago that the Earth is just a tiny spherical speck in a vast expanding Universe?
But if you still can't help being weirded out by all this, take consolation from a famous quote that has been attributed to Richard Feynman: "Anyone who claims to understand quantum theory is either lying or crazy."
You might also want to listen to our podcast, Does quantum physics really describe reality, featuring Roger Penrose and John Polkinghorne.
About this article
Nazim Bouatta is a Postdoctoral Fellow in Foundations of Physics at the University of Cambridge.
Tony Short is a Royal Society Research Fellow in Foundations of Quantum Physics at the University of Cambridge.
Marianne Freiberger is Editor of Plus. She interviewed Bouatta and Short in Cambridge in May 2012. She would also like to thank Jeremy Butterfield, a philosopher of physics at the University of Cambridge, for his help in writing these articles.
Comments
Anonymous
Three excellent papers, ready to be presented at under-graduation level in a diff. eq. course.
Specially the second one, it is the kind of elementary exposition that I regret not to find in Wikipedia.
Roberto Baldino
UERGS, RS, Brazil
Anonymous
I believe this to be misguided. The notion of wave-particle duality and the abstract mathematical solution to particle location probability is widely misunderstood, often incorrectly associated even by practising nuclear physicists. Experimentation show that there is indeed incidences where atomic particles behave like waves and sometimes like electrons such as in the primary dual slit experiment which exposed the problem. However, the wave-function of any given system ( a particle) is entirely a maths construct which yields usable results. These equations were originally applied to classical systems (sound waves, fluid motions, etc.) but by 'tweaking' them (taking the square of any primary classical wave function) it was realised they are applicable (usable) to describe multiple probabilities of where a particle may be positioned.
What this spawned was the notion of wave function collapse-a concept which has no practical proof and remains nothing more than an abstract. Alternate theories exist (each of about 5 concepts move in and out of 'fashion') which avoid the abstract idea of wave function collapse which itself is only a phrase which really is only applicable to the equation, not to the physical particle. We seem to be a world where the issues involving application of abstract wave functions to describe not-understood physical matter (as modelled by the notion of atoms and atomic structure) are being assigned to the physical systems our equations are good at predicting outcomes and making assumptions that the physical world owns the properties of the equations. They don't. No one on the planet with any real insight would suggest the wave function is 'real'. mol smith
Anonymous
When Erwin Schrödinger formulated his wavefunction equation, he was modeling a single particle that is presumed to have a position, (x,y,z) at every instant of time, t.
I don't understand what it means to apply Schrödinger's wavefunction formulation to a multi-particle system in which an ensemble of particles each have their respective positions at some given time, t. What is "system time" for a distributed system?
As I understand Relativity, one of the first things we learn is that there is no such thing as "system time" for a distributed system. Events separated in space cannot be said to be occurring simultaneously, because the notion of simultaneity breaks down in Einstein's model. Each particle in a distributed system is aging at its own idiosyncratic rate, according to its own clock. Modern atomic clocks can now measure the difference in timekeeping from moving a precision atomic clock just a few centimeters up or down in a gravitational gradient.
If there is no such thing as a common system time that pervades the universe, what does it mean to adapt Schrödinger's wavefunction to reckon a distributed system? What is John Bell supposed to plug in for time when computing his inequality?
Suppose Alain Aspect conducts his experiment at dawn on the day of the new moon — the day of spring tides. Suppose his apparatus is aligned east-west, so that one photon goes east, in the direction of the sun and the moon, while the twin photon heads west, in the direction away from the sun and the moon. There is a measurable gravitational gradient along their axis sufficient to produce spring tides on the planet. Do we still want to say that time ticks equally for the two photons? Suppose we let the two photons continue in their respective directions for 8 minutes, so that when one photon has reached the orbit of Mercury, the other photon is somewhere out near the Asteroid Belt. Now what? Does anybody really know what time it is?
Anonymous
'Some physicists, including Eugene Wigner and Roger Penrose, have toyed with the idea that a measurement requires an observer and that it is the consciousness of the observer that causes the collapse (which then begs the question of whether a snail, say, has enough consciousness to collapse a wave function).'
This is an instance in which the hegemonic, atheist paradigm seems to be an obstacle to the advancement of scientific understanding. The consciousness of a snail or any non-human animal would be of a different kind to that of a human being, which is evidently unique. I believe Eugene Wigner established in more than one way that we have a special place in the universe.
Sedumjoy
I believe you are confusing consciousness with measurement. A favorite pass time of quantum mechanics. The double slit experiment outcome has nothing to do with consciousness in the experimental sense of the word. When the measuring device is turned on then the wave pattern no longer appears but the particle appears in one spot or the other. There could have just as well been a timer turning on the measuring device while you were not in the room and the same thing would have happened. That being said consciousness does enter the picture but in a very subtle and unexpected place. Free will is usually tied to consciousness and if you don't believe in free will then there is no enigma because you could argue the universe conspired to set up the results knowing what your action was going to be. BUT if you believe in free will that the quantum enigma exists in the sense of the type measurement will predict a wave or a particle outcome. This is were consciousness meets QM.
Anonymous
OK, I get what Schrodinger's equation does. What equation is used to provide the information for how energy leaves the atom?
Anonymous
Are quantum fields ontologically real or are just a mathematical tool ?
Anonymous
I have a question which is kind of philosophical, since I am from a non-mathematical background.
Background- As I decipher from Schrodinger equation, small particles have discrete energy or quanta. And if we try to pin point their location at any given time, we can only determine a probabilistic position. I deduce that these particles are kind of independent of space-time, and that their space-time fabric at any given point will be probabilistic. In other words, there is no equation to define space-time fabric for small particles. Coming to Einstein's theory of general relativity which says that gravity results for changes in space-time fabric, and has a definitive equation for space-fabric.
Einstein has based his equations assuming a definite and continuous space.
Can you extend/ re-derive einstein's equation of general theory of relativity assuming a probabilistic space-time?
Analogy- Galaxies are moving away from each other. At any given point of time, position of a galaxy in only probabilistic, through we can determine position with a very high probability in this case.
Please can you provide your answer at manish.madnawat@gmail.com too
Thanks
aishleen
Why sigma bond is stronger than pie bond
Sherif Bagura
Sigma bonds are stronger than Pi bonds because electrons in Sigma bonds are localised, meanwhile in Pi bonds the elections are delocalised.
Lee Bloomquist
Hello. I am an outsider-- an engineer reading to keep brain working. As an outsider I feel compelled to interpret your interpretations. The language in this article about possibility seems to be translated into the language of complex numbers and the language of probability into the language of real numbers. As an outsider here is how that makes sense to me: Say that I want the possibility to win a raffle where one needs to be present to win. The possibility of me winning then involves (at least) two possibilities-- the possibility that I will own a ticket and the possibility that I will be present at the raffle. If either is zero, the possibility of my winning then becomes zero, or impossible. The language here is like the multiplication of two numbers-- if either factor is zero then the multiplicative product is zero. Now say that in the middle of the raffle, the rules change and one need not be present to win. In the language of numbers, this is like dividing the product of the two factors by one of the factors-- the factor translated into natural language that "one needs to be present to win." Factor that away from the multiplicative product, and the one factor that remains is the possibility of owning a ticket.
The natural language translation of words about possibility into the language of numbers therefore means the desired type of number to translate such sentences about possibility must be one of the "division algebras"-- real, complex, quaternion, or octonion. But which of these types?
Point: It doesn't matter which I say first in this "product"-- the possibility of being present or the possibility of owning a ticket. So the translation from natural language into the language of numbers must support multiplicative commutativity.
This rules out mathematical language involving the quaternions and the octonions as the language of choice for translating natural language about "possibility"-- because these types of numbers do not commute, multiplicatively.
So we are left for the candidates of translation of natural language about possibility either mathematical language involving the real numbers or mathematical language involving the complex numbers.
OK here is the next step: Logically, something either is a possibility or it is not a possibility. Whereas something may be more or less probable than something else.
Nothing is more or less possible than something else that is possible. Here are all the cases: (a) Both are possible. (b) One or the other is impossible. (c) Both are impossible. In this way natural language involving "possibility" is logical.
(Note: in natural language there are "connotations." Sentences about possibility "connote" information about probability. In this discussion I ignore these connotations.)
Again without these connotations, something can be more or less probable than something else that is probable. But nothing can be more or less possible than something else that is possible.
In terms of language about number, this translates into the "greater than/ less than" relation. Therefore normalized real numbers are appropriate for translating natural language about probability, since real numbers support the "greater than/less than" relation. And since complex numbers do not necessarily support the "greater than/less than" relation, mathematical language involving complex numbers supports translation into natural language about possibilities.
The Born rule is therefore a translation from language about possibilities (complex numbers, i.e., the wave function) into language about probabilities (the real numbers).
TEST: an interpretation of the Schrodinger equation.
Consider a free particle, where there is no energy potential as a function of configuration. In terms of physical displacement "x," there is in the Schrodinger equation a representation of momentum as the partial derivative of the wave function with respect to "x." And then this partial derivative is multiplied by the complex number "i."
I will attempt a translation of the mathematical language into natural language--
A factor multiplying by "i" -> "a possibility exists that"...
A factor of partial derivative of complex numbered function (the wave function) with respect to "x" -> "given a change in position "x," a change in possibility for existence at each location "x" will occur"
Product:
"a possibility exists that given a change in position "x," a change in possibility for existence at each location "x" will occur"
A possibility exists, so it is not necessary. Comparing this to Newton's laws, it is not necessary, but it is a possibility that at some future position "x" the particle in question will hit another particle. In the case of that possibility of hitting another particle, the possibilities for existence for the particle existing at all locations "x" will change.
Or, it is not necessary, but it is a possibility that at some future position "x," the particle in question will enter a field of potential energy depeding on "x." In which case, the possibilities for the particle existing at locations "x" will change.
So far this is just language about momentum. But the Schrodinger equation involves language about energy.
A change in energy, due to an impact with another particle, or due to entering a field of potential energy, means that there is the possibility (depending on changes in "x") of such changes in possibility.
Again, it's not necessary that there be an impact with another particle or that the particle enter a field of potential energy. But according to the Schrodinger equation, these are the possibilities.
http://fqxi.org/community/forum/topic/2420
israel socratus
Physics meets Psychology: determinism and free will.
===…
The Universe as whole is an infinite / eternal continuum: T=0K.
The infinite / eternal state is terrible boring state and therefore
quantum particles have only one will to change their state and
take part in the cosmic time-travel game, using of course these
well known physical-mathematical quantum and classical laws
and formulas to great a new Material World(s).
#
The nature by itself is rational and consists of particles and
their relations with each other. Everything can be explained
in terms of these particles and they relations.
Nature was created from simple to complex, from micro-levels
to macro-levels. At first these very small and thin quantum particles
created simple atom, then complex atom, then cell(s) . . then a monkey,
then a man. All was going according to the Darwin’s theory of evolution.
So, where is the problem between free will and determinism?
The problem is hidden in the border between two worlds:
Quantum and Material.
a)
Material Newtonian world obeys deterministic physical laws
(no place for free will) but Quantum world shows us indeterministic
behavior of particles (there must be freedom of the will)
b)
Newtonian physics explains action (movement) that was be evoked
by external forces. Quantum physics says that the cause of action
(movement) is its inner /own forces/impulses of particles.
Quantum particles have and use own/inner forces-impulses for actions.
c)
Border of determinism and free will can be seen in human beings.
Man want to act in his own subjective (sensual & logical) way and
his quantum particle want to stop and change his mistaken behavior.
Man has free will to choose his way:
a) to go by his own sense and logic . . . . or . . .
b) to go by quantum’s guide.
But usually we are ignored the quantum’s guide and as the
“Bhagavad Gita” says:
“Fools deride Me when I descend in the human form.
They do not know My transcendental nature and
My supreme dominion over all that be.”
/ Chapter 9. Text 11./
#
Inside each of us there is a quantum particle.
Today most scientists say that there isn’t consciousness on the
quantum level. But the quantum particles are indeterministic particles
and the least grain of information comes only from quantum particles
like photons/electrons. And until today there isn’t theory: what electron is.
1)
For example.
Book "What is the Electron?" by Volodimir Simulik . 2005. /
‘ More than ten different models of the electron are presented here. (!)
More than twenty models are discussed briefly. (!)
Thus, the book gives a complete picture of contemporary theoretical
thinking (traditional and new) about the physics of the electron.’
ftp://210.45.114.81/physics/%CA%E9%BC%AE/What%20Is%20the%20Electron%20b…
2)
Why does simple electron have six ( 6 ) formulas:
+E=Mc^2 and -E=Mc^2 , E=h*f and e^2=ah*c,
E=-me^4/2h*^2= -13,6eV and E= ∞ ?
Nobody knows their correlation, how to bind these formulas together.
3)
Robert Milliken, who measured a charge of electron, in his Nobel speech
( 1923) said that he knew nothing about “ last essence of electron”.
4)
“ It is important to realize that in physics today,
we have no knowledge of what energy is.
We do not have a picture that energy comes in little
blobs of a definite amount. “ / Feynman. 1987 /
(energy “in little blobs of a definite amount” is an electron)
Therefore someone said:
“ We know electron by what it does, not by what it is.”
It is very a pity, but electron (and photon) is still an enigma today.
#
Philosopher John Searle wrote:
“ . . ., it looks as if we would have to postulate that inside each of us
was a self, that was capable to interfering with the causal order of nature. . . . .
. . .but it’s certainly not consisted with what we know about how the
world works from physics. And there is not the slightest evidence
to suppose what we should abandon physical theory in favor of such a view”
/ “The freedom of the will”, part (other possible solutions) , by John Searle./
#
In my opinion the other possible solution ( inside each of us there is quantum
particle- electron/photon - owner of self-action) seems crazy today but the
rational logic says that we need to reconsider our view on Physics.
=====…
Book: The Holographic Universe, page 6, by Michael Talbot.
''Science is not always as objective as we would like to believe.''
/ Michael Talbot/
#
"One thing I have learned in a long life:
that all our science, measured against reality, is primitive
and childlike - and yet it is the most precious thing we have."
/Einstein./
======…
Best wishes.
Israel Sadovnik Socratus
=============
Sedumjoy
The top picture of the Solvay conference ...why wasn't Enrico Fermi there, after all wasn't he the "Pope of Physics". Rather strange since he was a key player in Quantum Mechanics
Sedumjoy
I disagree with the author , The Many Worlds Interpretations adds more baggage not simplicity. You have to all of a sudden add an infinite number of new universes. That's a lot of baggage. and a lot of new rules for how many universes are enough. At the quantum scale the states of each and every particle in existence can be said to take alternate universes so how is it decided how many are enough to complete the set for each particle. Add that the fact that the particle may actually be an excitation of a field and then that adds even more baggage or should I say garbage...which is what it probably is.