
Solving crimes with maths: Bloodstain pattern analysis
Countless movies and TV dramas have taught us the importance of crime scene investigation. What's less well-known, though, is the fact that maths has an important role to play in this. In this article we'll explore how basic trigonometry is used in this context.
How do bloodstains tell us where a crime is committed?
Bloodstains provide a lot of clues about what happened on the crime scene. Bloodstain pattern analysis (BPA) is the interpretation of bloodstains at a crime scene to recreate the actions that caused bloodstains. Elements of biology, physics, and mathematics are used to help determine the source of blood and the positions of the victim and perpetrator.
We will be looking at impact stains and passive stains. Impact stains result from blood projected through the air, whereas passive stains result from the effect of gravity on a body. These can result from stabbings, beatings, and gunshot injuries.
When blood droplets strike a surface, the shape of the bloodstain depends on the angle of impact and the distance travelled.
Direction and distance
The shape and tail of the bloodstain indicates the direction the blood was travelling in. Imagine there are three bloodstains on the floor, as shown in the diagram below. Also imagine all these stains came from the same source (e.g. someone being hit over the head).
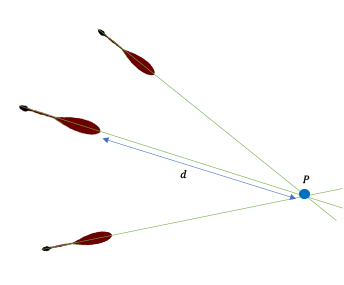
Looking down at three bloodstains on the floor. The source of the blood will be somewhere vertically above P.
The angle of incidence
If blood were to drop vertically down onto a smooth surface, so that the trajectory of the blood makes a 90° angle with the surface, it would create a circular shaped drop. If blood were to drop obliquely to the floor, at an angle less than about 70°, it would form an elliptical shape with a tail.
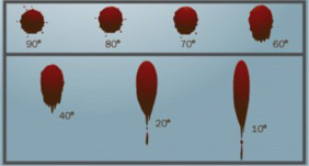
Shape of bloodstain for different angles of incidence.
Investigators can measure the length, $a$, and width, $b$, of the bloodstain:
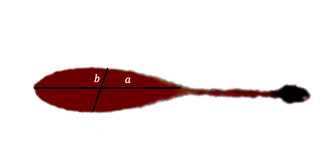
Measuring width and length of the bloodstain.
They can then calculate the angle at which the blood drop hit the surface, which is called the angle of incidence, with the help of a right-angled triangle, using this diagram:
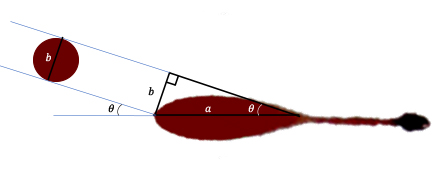
Calculating the angle of incidence.
Here a blood droplet travels towards a surface with the angle of incidence equal to $\theta$. The diameter of the droplet before impact is assumed to be equal to the width, $b$, of the droplet (this may not be exactly true in reality but provides a good approximation). By moving this diameter as shown, we can form a right-angled triangle. The width, $b$, is opposite the angle $\theta$ in this triangle and the length $a$ is the hypotenuse. We therefore have $$\sin{(\theta)} =\frac{b}{a}.$$ Since we know $a$ and $b$ from measuring the bloodstain, we can work out $\theta$ as $$\theta=\sin^{-1}{\left(\frac{b}{a}\right)}.$$
The height of the source
We are now ready to calculate the height of the source of the bloodstains. We can form a right-angled triangle whose sides are the line from one of our bloodstains to the point $P$ we identified earlier, the line that goes vertically up from $P$ at right-angles to the flood, and the line starting at the bloodstain and forming an angle $\theta$ with the floor.
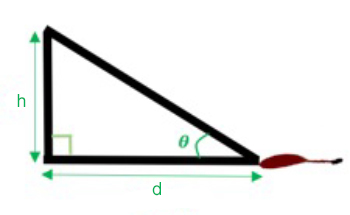
Calculating the height of the source
The height $h$ of the vertical line is given by $$\frac{h}{d} =\tan{( \theta)},$$ so $$h=d\tan{( \theta)}.$$ Since we know the value of $\theta$ and the distance $d$ (see the first figure above), we can work out $h$, the height of the source. If you already know for example, that the blood comes from a victim being hit over the head, this information can indicate whether the person was standing up while this happened, or was beaten while already lying on the floor.
The outputs produced with blood pattern analysis can be used to corroborate witness statements and laboratory findings. It is surprising that something as basic as trigonometry can tell us a lot about what happened at the crime scene.
You may also want to read Solving crimes with maths: Busting criminal networks by Marcia Gomez.
About the author

Marcia Gomez is a recent Maths and Economics graduate from the University of Bath, who is particularly interested in statistics and how maths is used in the real world. She is currently applying her knowledge in the world of finance.
Comments
Mic
How can i measure the distance ?