As we saw in the first part of this article, in 1850 George Gabriel Stokes came up with an efficient way of approximating Airy's function, which helped to understand the supernumerary fringes of the rainbow. But although he had solved the practical problem, Stokes wasn't happy. His approximation to Airy's function was asymptotic, meaning it only worked for sufficiently large positive, or sufficiently small negative, values of the variable $x$. At $x=0$ the approximation shoots off to infinity.

This in itself wasn't the problem. The asymptotic approximation was good enough for the purpose of the supernumerary arcs. What bothered Stokes was that the two parts of his approximation were represented by two very different mathematical expressions. The figure below shows the Airy function (blue) and the approximation (red) together with two expressions for the red function which come from Stokes' approximation (the approximation uses series, and the expressions shown come from just considering the first term of the series).

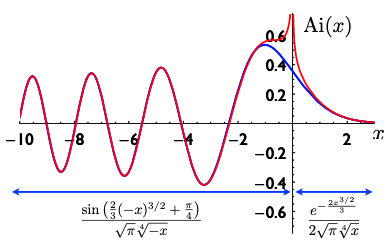
The blue curve is the actual Airy function and the red curve Stokes' asymptotic approximations. The formulae give the descriptions of each part of the approximation. This figure is from a talk by Chris Howls and Adri Olde Daalhuis that was given given at the Isaac Newton Institute.

As you can see, the expression for $x>0$ involves one exponential term while the expression for $x0$ involves a sine function. If you know these functions then this will make sense to you. The red curve on the right of $x=0$ comes down from infinity and rapidly decays towards $0$, which is exactly what you'd expect for an exponential expression with a negative exponent. The red curve on the left of $x=0$ oscillates up and down, and oscillations are what you expect from a sine function.

Now it turns out that (venturing into the land of complex numbers) a sine function can be expressed as a sum of two exponential functions (see the box on the right). Thus, we have one exponential for $x>0$ and two exponentials for $x0$, even though Airy's original function exhibits no such difference for negative and positive values of the variable. "What Stokes wanted to know was, how do you get one [exponential] vanishing if you go from negative to positive, and if you go the other way, how do you get one being born?", says Howls.

Going up a dimension

Now obviously, things get messy at the point $x=0$: there is a singularity where both components of the approximation shoot off to infinity. Arguably anything could happen at infinity, exponential terms could die or they could be born, so maybe the phenomenon isn't so surprising.

However what Stokes had done, which was quite revolutionary at the time, is to consider his approximation to be a function of a complex variable. If you don't know what complex numbers are, you can think of this in terms of going up a dimension. The real numbers merge together to form a line, and a function of a real variable allocates to each real number (i.e. point on that line) another real number. Complex numbers can be taken to represent points on the two-dimensional plane, and a function of a complex variable allocates to each complex number (i.e. point on the plane) another complex number. The real numbers are represented within the complex number as a line sitting inside the plane, so the complex numbers can be viewed as an extension of the real numbers — and a complex function as an extension of a real function. (See here for an introduction to complex numbers.)

The figure below shows the complex plane, as it is called, with the real line sitting within it. A function of a complex variable takes a point on this plane as input and returns another point on this plane as output. We can't plot the graph of such a function because we would need four dimensions: two for the input of the function and two for the output.

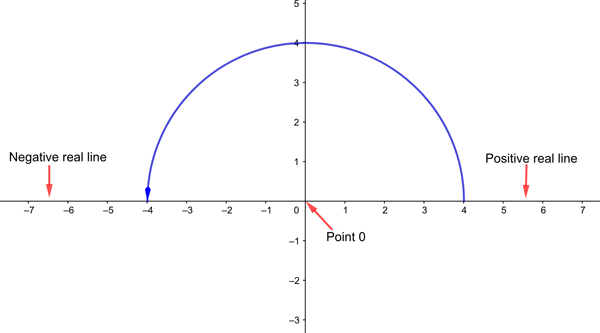
The complex plane with the real line sitting within it, represented by the horizontal axis. To go from the positive part of the real line to the negative one, you don't have to go through the point 0. You can also walk around a semicircle, like the one shown in blue.

Once you are working on the plane, rather than just with the real line, there is more than one way to go from the positive part of the real axis to the negative part. You can avoid the singularity at the point corresponding to the real value $x=0$ by going around it, say in a semicircle (such as the one on blue shown in the figure above). The question is, where and how along this journey could an exponential term be born?

Jumping coefficients

A few years after Stokes's first publication on Airy's function, he came up with a partial answer to this question. The maths here is complicated, so we just give the general gist. Essentially, Stokes was dealing with an asymptotic approximation of a function of a complex variable $z$ which involved the sum of two exponential terms, each multiplied by a coefficient and a divergent series. In other words, he was dealing with something that looked like

\begin{eqnarray*} & A \times (\mbox{exponential term involving $z$}) \times (\mbox{divergent series involving $z$}) \\ + & B \times (\mbox{another exponential term involving $z$}) \times (\mbox{another divergent series involving $z$}).\end{eqnarray*}

Now if the series involved were convergent, then the values of the coefficients $A$ and $B$ would be the same for all points $z$ on the plane. This means that, as long as neither $A$ nor $B$ are equal to $0$, you would always be looking at two exponential terms. But when divergent series are involved more things are possible. Stokes realised that in this case, the coefficients are able to jump in value. In particular, a coefficient could be equal to $0$ in one part of the plane, meaning your asymptotic approximation only involves one exponential term there, and non-zero in another part of the plane, giving you a sum of two exponential terms in that region — which is exactly what happens with Airy's function.

This propensity of coefficients within asymptotic approximations to change their value is what is known as Stokes' phenomenon.

(Indeed, Stokes found that the coefficients in his expression were not only able to jump, they had to jump. One condition the asymptotic approximation should definitely satisfy is that if you start at some value of $z$ on the positive real line and then walk once around the point $0$ describing a full circle taking you back to $z$, then the value of the approximation should also return to the value it took at $z$ when you started. Stokes noticed that the only way this could happen, was if the values of the coefficients jumped. This is related to the fact that his expression contained roots of the complex variable, which are multi-valued — find out more here.)

Stokes lines

Having established that the coefficients have to change their values somewhere on the plane, Stokes set out to see where those jumps occurred. He realised that, if you consider the two terms in the expression

\begin{eqnarray*} & A \times (\mbox{exponential term involving $z$}) \times (\mbox{divergent series involving $z$}) \\ + & B \times (\mbox{another exponential term involving $z$}) \times (\mbox{another divergent series involving $z$}).\end{eqnarray*}

separately, and see what happens to them as the variable $z$ moves along a circle around the point 0, you find that the exponentiations take turns at having a large absolute value and a small absolute value: while one term is superior, the other is inferior and vice versa. (This is related to whether the term in the exponent of the exponential have a positive or a negative real part.)

A jump in the value of a coefficient must not affect the mathematics the asymptotic approximation as a whole needs to satisfy — if a new exponential term is going to come in because its coefficient is switched from zero to non-zero, then this should happen where it's the least noticeable. This is why Stokes figured that a jump could only occur at points where the switching coefficient in question belongs to an inferior term and the superior term is at its largest.

"What Stokes said was, when [the superior term] is at its largest that's where other exponentials could drop in," explains Howls. "In terms of numerical approximation, if you are going to add something in, it's best to add it in at the point where the most dominant term is the largest and the thing you are adding is at its smallest."

In the case of Airy's function, Stokes worked out that the places where a small exponential could be smuggled in was at the lines shown in the diagram below, which are known as Stokes lines. They form angles of 120 and 240 degrees with the positive real line, going anticlockwise.

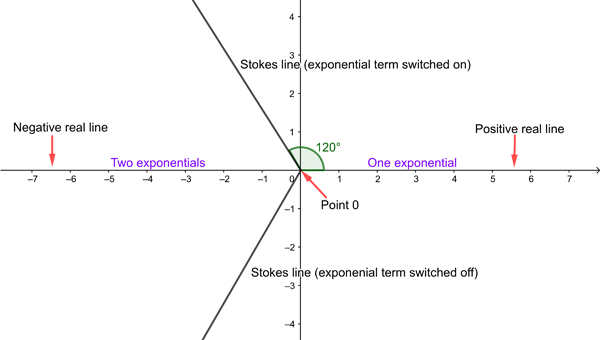
Imagine starting on the positive real line and walking anticlockwise along a circle. As you start off your asymptotic approximation features just one small exponential term, which keeps growing until you reach the Stokes like at angle 120 degrees, where it is maximal. Here the second small exponential is switched on and starts to grow, so that by the time you get to the negative real line both exponential terms are contributing to the value of the approximation. When you reach the second Stokes like at 240 degrees, one exponential is switched off again.

"As you go around [starting from the positive real line] the exponential which is decaying on the positive real line starts growing in magnitude," explains Howls. "By the time you get to the [120 degree Stokes line] it has become exponentially large," explains Howls. "If you then switch on the other small exponential as you cross the Stokes line, and move around to [the negative real axis], they are both of the right order to combine to give you the right sinusoidal behaviour."

More questions

As Stokes himself knew, the phenomenon now named after him did not just occur for Airy's function, but for a whole class of other functions too. Such functions, and their asymptotic approximations, are bread-and-butter in applied mathematics and theoretical physics. When you are applying this type of mathematics to a real-world problem, you really don't want exponentially terms being born without you noticing. "They may be exponentially small in one region, but in another region they can grow again," says Howls. "That's why you have to take them into account."

Stokes had only demonstrated that it's possible for exponential terms to be born, and where they could be born, but he hadn't shown the mathematical workings of exactly how they are born. This question was picked up again over 100 years after Stokes' explanation, and is still being studied today. Find out more in the article The power of small things.

About this article

This article relates to the Applicable resurgent asymptotics research programme hosted by the Isaac Newton Institute for Mathematical Sciences (INI). You can see more articles relating to the programme here.

Marianne Freiberger is Editor of Plus. She interviewed Chris Howls in July 2021.

This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.