
Too big to write but not too big for Graham
Recently, when we were writing our book Numericon, we came across what has now become one of our very favourite numbers: Graham's number. One of the reasons we love it is that this number is big. Actually, that's an understatement. Graham's number is mind-bendingly huge.

The observable Universe is big, but Graham's number is bigger. Image: ESA and the Planck Collaboration.
Our new favourite number is bigger than the age of the Universe, whether measured in years (approximately 14 billion years) or seconds (4.343x1017 seconds). It's bigger than Avogadro's number, a sizeable 6.02214129 x 1023. This is the number of hydrogen atoms in 1 gram of hydrogen, which is called a mole and is the standard unit for measuring an amount of a substance in chemistry or physics.
Graham's number is bigger the number of atoms in the observable Universe, which is thought to be between 1078 and 1082. It's bigger than the 48th Mersenne prime,
257,885,161-1,
the biggest prime number we know, which has an impressive 17,425,170 digits. And it's bigger than the famous googol, 10100 (a 1 followed by 100 zeroes), which was defined in 1929 by American mathematician Edward Kasner and named by his nine-year-old nephew, Milton Sirotta. (This might sound familiar, as Google was named after this number, though they got the spelling wrong.)
Graham's number is also bigger than a googolplex, which Milton initially defined as a 1, followed by writing zeroes until you get tired, but is now commonly accepted to be 10googol=10(10100). A googleplex is significantly larger than the 48th Mersenne prime. You, or rather a computer, can write out the 48th Mersenne prime in its entirety, all 17,425,170 digits of it. But, despite the fact that I can tell you what any digit in the googolplex is (the first is a 1, the rest are all 0), no person, no computer, no civilisation will ever be able to write it out in full. This is because there is not enough room in the Universe to write down all googol+1 digits of a googolplex. As Kasner, and his colleague James Newman, said of the googolplex (in their wonderful 1940s book Mathematics and the imagination which introduced the world to these numbers): "You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way."
Graham's number is bigger than the googolplex. It's so big, the Universe does not contain enough stuff on which to write its digits: it's literally too big to write. But this number is finite, it's also an whole number, and despite it being so mind-bogglingly huge we know it is divisible by 3 and ends in a 7.
A big party
The origins of Graham's number go back to 1928 when a brilliant young mathematician, Frank Ramsey, noticed a surprising thing when he was working on a paper about logic: complete disorder seemed to be impossible. No matter how complicated your system looks, pockets of order of any size are always guaranteed to be there if the system is large enough.
This result, which was just a small part of the particular paper he was working on, was the start of a whole new field of mathematics called Ramsey Theory. This area of maths is often explained with the example of a party. Suppose you're having a party and you want to make sure you invite a good mix of people and decide to keep track of who knows who. Suppose you draw a map of the relationships of all your friends, linking two people with a blue edge if they are friends and with a red edge if they are strangers. Then you might end up with something like this:
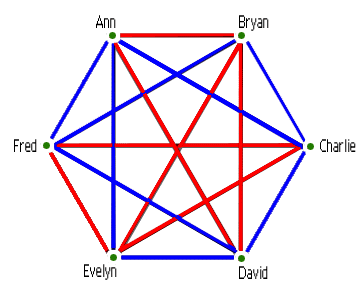
Now this looks pretty complicated and it would take quite a lot of information to describe who is connected by red edges and who is connected by blue edges. But if you zoom in on just Ann, Bryan and David, they are all joined by red edges. This red triangle is an example of order hiding in the messy overall network. The more ordered a system is, the simpler its description. The most ordered friendship network is one that has all the edges the same colour: that is, everyone is friends or everyone is strangers.
Ramsey discovered that no matter how much order you were looking for – whether it was three people who were all friends and strangers or twenty people who were all friends and strangers – you were guaranteed to find it as long as the system you were looking in was large enough. To guarantee yourself a group of three people who are all friends or all strangers you need a friendship network of six people: five people isn't enough as this counterexample shows.
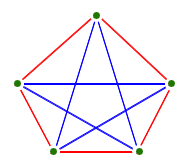
The number of people you need to guarantee that you'll find three friends or three strangers is called the Ramsey number R(3,3). We know a few Ramsey numbers: we've seen that R(3,3)=6, and it has been proved that R(4,4), the number of people you need to guarantee you'll find four friends or four strangers, is 18. But we hit a wall very quickly. For example we don't know what R(5,5) is. We know it's somewhere between 43 and 49 but that's as close as we can get for now.
Part of the problem is that numbers in Ramsey theory grow incredibly large very quickly. If we are looking at the relationships between three people, our network has just three edges and there are a reasonable 23 possible ways of colouring the network. For four people there are six edges and 26=64 possible colourings. But for the relationships between six people there are fifteen edges and we already have to consider an unwieldy 215=32,768 possible colourings. Mathematicians are fairly certain that R(5,5) is equal to 43 but haven't found a way to prove it. One option would be to check all the possible colourings for a network of 43 people. But each of these has 903 edges, so you'd have to check through all of the 2903 possible colourings – more colourings than there are atoms in the observable Universe!
Too big to write but not too big for Graham
Big numbers have always been a part of Ramsey theory but in 1971 mathematician Ronald Graham came up with a number that dwarfed all before it. He established an upper bound for a problem in the area that was, at the time, the biggest explicitly defined number ever published. Rather than drawing networks of the relationships between people on a flat piece of paper as we have done so far, Graham was interested in networks in which the people were sitting on the corners of a cube.
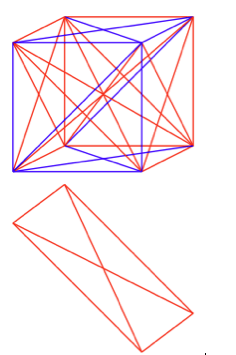
In this picture we can see that for a particular flat diagonal slice through the cube, one that contains four of the corners, all of the edges are red. But not all colourings of a three-dimensional cubes have such a single-coloured slice. Luckily, though, mathematicians also have a way of thinking of higher dimensional cubes. The higher the dimension, the more corners there are: a three-dimensional cube has 8 corners, a four-dimensional cube has 16 corners, a five-dimensional cube has 32 corners and so on. Graham wanted to know how big the dimension of the cube had to be to guarantee that a single-coloured slice exists.

Ronald Graham who gave us his beautiful number. Image: Cheryl Graham.
Graham managed to find a number that guaranteed such a slice existed for a cube of that dimension. But this number, as we mentioned earlier, was absolutely massive, so big it is too big to write within the observable Universe. Graham was, however, able to explicitly define this number using an ingenious notation called up-arrow notation that extends our common arithmetic operations of addition, multiplication and exponentiation.
We can think of multiplication as repeated addition:
3 x 3 = 3+3+3
33 = 3 x 3 x 3.
If we define the single arrow operation, ↑, to be exponentiation, so:
3↑3 = 33 = 3 x 3 x 3 = 27,
then we can define the double-arrow operation ↑↑ to be
3↑↑3 = 3↑3↑3 = 333 = 327 = 7,625,597,484,987.
We can carry on building new operations by repeating previous ones. The next would be the triple-arrow
3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑↑3)=3↑↑7,625,597,484,987
a tower of powers of 3 that is 7,625,597,484,987 levels high! (See here to read about the up-arrow notation in more detail.)
The number that has come to be known as Graham's number (not the exact number that appeared in his initial paper, it is a slightly larger and slightly easier to define number that he explained to Martin Gardner shortly afterwards) is defined by using this up-arrow notation, in a cumulative process that creates power towers of threes that quickly spiral beyond any magnitudes we can imagine.
But the thing that we love about Graham's number is that this unimaginably large quantity isn't some theoretical concept: it's an exact number. We know it's a whole number, in fact it's easy to see this number is a multiple of three because of the way it is defined as a tower of powers of three. And mathematicians have learnt a lot about the processes used to define Graham's number, including the fact that once a power tower is tall enough the right-most decimal digits will eventually remain the same, no matter how matter how many more levels you add to your tower of powers. Graham's number may be too big to write, but we know it ends in seven. Mathematics has the power not only to define the unimaginable but to investigate it too.
About this article

Rachel Thomas and Marianne Freiberger are the editors of Plus. This article is an edited extract from their new book Numericon: A journey through the hidden lives of numbers.
Comments
Anonymous
Graham’s number is so mind boggling that I have reread this article a few times. Doing so today I see I don’t quite understand the Arrow notation. 3^^3=3^(3^3)=3^27. OK
now the question is how does the expansion for different numbers work. if 4^^3=4^(4^4), then is 3^^4=3^((3^3)^3)?
but isn't that 3^(3^(3^3))= 3^^^^3 ?
Basically I thought the number of up arrows controlled the expansion, but now I think I’m wrong.
I’m posting rather than email because i thought others might have the same confusion.
Anonymous
Think the number to the right of the arrow is the exponent: 4^^3 = 4^(3^3) = 4^9 etc.
Bognár Erik József
What are those things?
Unilo
Googolplexitoll, Googolplexigong is larger than googolplex.
We have Kilotar, Dekotar, and a silly number BIG FOOT. That is FOOT(10V100). Omega is even larger than infinity!
I AM JUST IN GRADE 1!
les go
well it's widespread and popular so it's not that hard to find out about these concepts of "oH wOw i fOuNd tHiS nUmBeR [so on]" sorry if this sounded rude i didn't mean it
>-<
Omega is larger than infinity that's crazy, does it go on or is omega the largest thing known to humanity?!?
Aaron
Well, it should be noted that it is still AN infinity, but I think what the poster meant is that it is larger than the smallest infinity, which is true. It is not the largest possible infinity and several larger infinities have been defined.
Mason
What things?
Julian65535
4^^3 is 4^4^4 = 4^16 = 2^32 = 4 billion lol
jamyia
the number is pronounced as..........
seven trillion --- six hundred twenty five billion --- five hundred ninety seven million---- four hundred eighty four thousand ---- nine hundred eighty seven
7,625,597,484,987
reply plz :)
Peter Jewell
People are often confused about the size of Grahams number. They don’t understand the mind boggling power of the up arrow notation. If you try to imagine infinity itself it’s nothing in comparison to Grahams number. Your brains perception of infinity is zero compared to the number of digits required to write the number of levels of mathematical operation after addition and exponentiation etc in order to get to the first few steps on the path to G64 which is Grahams number
tsunami
4^^3 is 4^(4^4) or 4^256. It's 4 raised to itself 3 times.
Anonymous
4 x 3 = 4 + 4 + 4
4 ^ 3 = 4 x 4 x 4
4 ^^ 3 = 4 ^ 4 ^ 4
4 ^^^ 3 = 4 ^^ 4 ^^ 4
4 ^^^^ 3 = 4 ^^^ 4 ^^^ 4
They all follow the same pattern. For up arrows, you just have one less up arrow than in the original problem.
You are correct that
3 ^^ 4 = 3 ^ 3 ^ 3 ^ 3
However,
3 ^^^^ 3
is actually = 3 ^^^ (3 ^^^ 3)
Working on the parentheses first, you'd find that (3 ^^^ 3) = 3 ^^ (3 ^^ 3)
Again, working on the parentheses, (3 ^^ 3) = 3 ^ 3 ^ 3 = ~7.6 trillion. Put that back in your other problem
and you've got 3 ^^ (~ 7.6 trillion), which means you're doing 3 ^ 3 ^ 3 ^ 3... until you've done it 7.6 trillion times.
Once you get that crazy huge number, you'd put it back in the original problem:
3 ^^^ (crazy huge number).
Which is 3 ^^ 3 ^^ 3 ^^ 3... until you've done it a crazy huge number of times. Unimaginably big. And that's only with only 4 up arrows.
The epic boss
If 3^^^^3 is called g1 than you get 3 g1 number of ^ 3 and that becomes g2 repeat that until you get g64 and that is one Graham's Number
Dougy
Thanks for posting the correct definition.
People should NOT comment unless they know what they are talking about. If you take a little time and watch Numberphile on YouTube,
you can see Graham himself define the number.
Your explanation was the correct one. Thank you for not saying something stupid.
Anonymous
10ⁿ⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰∅⁰⁰⁰⁰⁰0¹⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰ it has Googlcomplex zeros
Anonymous
Ok I had the same problem for a while too understanding how arrows worked but it’s actually a rather simple pattern just different from how we’re used to thinking about operations.
Basically the number of arrows tell you the amount of times you repeat the operations that come before it.
Imagine for a second instead of using arrows the (+) sign in addition behaved in the same way the arrows did.
3+3=6
no problems but
(3++3)=(3+(3+3))=3x3=9
If addition behaved exactly like the arrows then
(3+++3)=3^3
And
(3++++3)= 3^^3
Long story short the arrow just tells you to take the process used for the previous number of arrows and use a repeated form of that.
Anonymous
3^^4 = 3 ^ ( 3 ^ ( 3 ^ 3 ) )
3^^^^3 = 3 ^^^ ( 3 ^^^ 3 )
Oscar
The fact that in arrow notation my I(x) would equal x⬆️⬆️x+1
Aiden
3^^4=3^(3^(3^3))=3^(3^27)...
So work on it step by step
Also,3^(3^(3^3))DOESN'T EQAUL3^^^^3
Anonymous
So 3^^3 is a power tower of 3s, 3 high, so 4^^5 is a power tower of 4s, 5 high. 3^^^3 is a power tower feeding frenzy, where there are 3 towers (because of the second three) and they all have the same base number (3, because of the first three). The difference between the towers is the height. The first tower is 3 high (the same as the base number), and once that is multiplied out, that is the HEIGHT of the next one. This continues forth. This also means that 4^^^5 (for example) would be 5 towers of 4s, the first one being 4 high. 3^^^^3 is a power tower feeding frenzy psycho festival, where there are 3 feeding frenzies (because of the second three). Once the final number in the first frenzy is multiplied out, that becomes the NUMBER OF TOWERS in the second frenzy (the first beginning with the height of the base number). This means that our 4^^^^5 example would be 5 frenzies, each with a base number of 4. This doesn't continue onwards in Graham's number (since he made 3^^^^3 into g1) but 3^^^^^3 would be a power tower feeding frenzy psycho festival national celebration, where there are 3 FESTIVALS, each finishing number being the number of frenzies in the next one. It just iterates upwards.
Note: This might not have clarified anything, just wanted to say it to try and help :)
12
3^^3 is a power tower of 3s.
4^^5 is a power tower of4s and 5s.
3^^^^^3, 4^^^^5 doesn't count to Graham's number.
Note: Try it:)
Parker Beebe
I was also confused about this i had read the article many times but could not understand that part
Anonymous
Great explanation, but I'm somewhat puzzled by the fact that you never actually told us how Graham's number is defined. It's like there's a missing paragraph after you finish explaining the rapid recursive growth of up-arrows.
As I understand it, you start with 3^^^^3,
i.e. 3^^^(3^^^3)
i.e. 3^^(3^^(3^^3))
i.e. 3^^(3^3^3^3^3^3^3...) where "..." continues on for 3^3^3 iterations of powers of three
i.e. 3 raised to the third power a number of times equal to (3^3^3^3^3^3^3^3...) from above
i.e. already an unimaginably large number.
You start with the end result of that, then put that many *up arrows* in between two threes. That is to say that after we just got that huge number result that I can't concisely describe from just 3^^^^3, we look at the number 3^^^^^...3 that has that indescribable number of ^'s in it. That's "Step 1".
Then you do it again; take the number from Step 1, and put *that many* ^'s between two threes. Well beyond numbers anyone can really hope to imagine in any meaningfully representative way without deep mathematical understanding, this completes Step 2.
Graham's Number is the result when we reach Step 64, each of these steps involving putting a number of ^'s equal to the value of the previous step in between two threes.
Anyway, that's what I think an explanation might look like; I'm surprised something like this wasn't included. Otherwise, great explanation,
Anonymous
Hi. This article, though clarifying Knuth's "Arrow Notation", doesn't get you to Graham's Number. Graham went one step further. To get to G (Graham's Number), one starts with 3^^^^3 (a clearly demonstratedly STOOPID BIG number. However, that number is called "g1". Now, take 3^...^3, where "^...^" is g1 ^'s. That is "g2". Following the pattern, "g3" is made of "g2" ^'s. Are you sitting down? Graham's Number is g64!!!
↑
Instead of ^ (which is commonly know as "to the power of") use this ↑.
They are not the same thing.
David upchurch
Actual up arrows shouldn't be shown in it because (like you said) they don't mean the same thing. B.T.W (by the way) you just made a argument waiting to happen by saying "They are not the same thing." SO, PEOPLE USE THIS -------> ^!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
JEEZ!!!!!
Michael Ossipoff
Someone said:
"Instead of ^ (which is commonly know as "to the power of") use this ↑.
They are not the same thing."
Incorrect. When it has been specified that "^" is being used to stand for Knuth's up-arrow, then yes, it becomes the same thing.
Unless a computer keyboard has the up-arrow, it's necessary to substitute something else for it.
A good reason why "^" is a good substitute is the fact that one up-arrow means the same as "^": Exponentiation.
Therefore, "^" is the natural and obvious substitute for the up-arrow, if the computer keyboard doesn't have the up-arrow.
Michael Ossipoff
Wayne Lee
If it really bothers me to substitute the caret ^ for the up arrow ↑ I just hold the Alt key down and tap 2 then 4 on the numeric keypad then release the Alt key. This produces the character "↑" which looks like an up arrow to me.
videogame27
Yeah graham's number is huge, but not as big as a googolplexian, which is a one followed by a googolplex number of zeros. In fact, the googolplexian is the largest number that has a name.
No Comment
a googleplexianth is 1 followed by a googleplexian zeros. in which grams number is still larger. 3^3 quadrillions of times does in fact add up rather quickly.
VeggieBoi
Googolplexian is nothing compared to Graham's number since googlplexian is merely 10^10^10^100 while it is already dwarfed by the first iteration for Graham's number (3 ↑↑↑↑ 3 = 3 ↑↑↑ 7,625,597,484,987)
Year 7 student
Man I was curious about googol then I stumbled on googolplex then I noticed it was only the 2nd biggest number according to google then I found out about grahams number bloody hell i f I ever get cocky about my intelligence I'll just think about grahams number and think about how confusing it is man I don't think I'll be able to sleep at night I wish I had just stuct to studying pi multiplied by the radius squared
Tom
Actually, Graham's number is now considered pretty small by mathematicians. For example, TREE(3) is so big that it makes Graham's number look like pretty much like zero in comparison. The interesting thing about the TREE function is that it grows so rapidly eg.
TREE(1) = 1
TREE(2) = 3
TREE(3) = something insanely big!
Anonymous
How does that even work?
Anonymous
Imagine TREE(TREE(3))
QuantumCrash
Graham's Number = G
^ = up arrow
Do G ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^G
That number is DEFINITELY bigger than TREE(5)
Jordan
I don't think so, but I didn't count the arrows. Is it G<100>? Big, but I think it doesn't approach Tree(5). See Numberphile -- Tree(G64) for a really fun and technical explanation of where they fall in the infinity system.
This does not count SCG(13), Loader's number, Rayo's number, (Big)Foot's number ... or Busy Beaver.
jayne sturge
even tree[treeG1000] is puny to my number
Peter Jewell
What is your number?? Please explain!! I’m interested. My number is 07523935469
Anonymous
VERY RIDICULOUS!TREE(3)>>>that number
Lord Beerus
Your number is not Big enough to Beat TREE(3).
Forget about TREE(3), your number isn't even bigger than G(65) which is Grahams number followed by G(64) number of arrows in between them.
A grahams number growth rate is not more than fw+1 while there are not enough finite ordinals to represent growth rate of TREE(3).
Even if you write G(G(G(G(G...G(64)))) with G64 times and then make power tower of this number to another G(64) times, you still is hasn't approached to TREE(3) yet, not even close. You still a zero.
Anonymous
SSCG.SSCG(0)=2 SSCG(1)=5 SSCG(2)>3x(2^(3x2^95))=10^(3.5775x10^28) SSCG(3)>>>TREE(3) SSCG(3)>>TREE(TREE(TREE(...(TREE(3))..) TREE(3) times
j
my story is the EXACT SAME!!!!!!!!! OK nonononono the simplest explanation is GOOGLEPLEXIANTH
1e+googolplexth power. Up arrow is nothing
monty sturge
i have created a number bigger than the puny G64
Oscar
How does it work?
Anonymous
No you are wrong a googleplex^of a googleplex is smaller than graham but larger than googleplex
Behrad
i have something bigger it is 10^10^googolplex^10
Confused
Statements such as the universe itself isn't large enough to write down Graham's number would mean more if the font size the writer is using was mentioned. What is the smallest font permitted? How many peas you could put in a bottle depends on the size of the bottle and the size of the pea.
Iain
If each character was no larger than 1 Planck length, still wouldn't even make a dent.. Absolutely mind dissolvingly, unfathomably, ludicrously large.