
Too big to write but not too big for Graham
Recently, when we were writing our book Numericon, we came across what has now become one of our very favourite numbers: Graham's number. One of the reasons we love it is that this number is big. Actually, that's an understatement. Graham's number is mind-bendingly huge.

The observable Universe is big, but Graham's number is bigger. Image: ESA and the Planck Collaboration.
Our new favourite number is bigger than the age of the Universe, whether measured in years (approximately 14 billion years) or seconds (4.343x1017 seconds). It's bigger than Avogadro's number, a sizeable 6.02214129 x 1023. This is the number of hydrogen atoms in 1 gram of hydrogen, which is called a mole and is the standard unit for measuring an amount of a substance in chemistry or physics.
Graham's number is bigger the number of atoms in the observable Universe, which is thought to be between 1078 and 1082. It's bigger than the 48th Mersenne prime,
257,885,161-1,
the biggest prime number we know, which has an impressive 17,425,170 digits. And it's bigger than the famous googol, 10100 (a 1 followed by 100 zeroes), which was defined in 1929 by American mathematician Edward Kasner and named by his nine-year-old nephew, Milton Sirotta. (This might sound familiar, as Google was named after this number, though they got the spelling wrong.)
Graham's number is also bigger than a googolplex, which Milton initially defined as a 1, followed by writing zeroes until you get tired, but is now commonly accepted to be 10googol=10(10100). A googleplex is significantly larger than the 48th Mersenne prime. You, or rather a computer, can write out the 48th Mersenne prime in its entirety, all 17,425,170 digits of it. But, despite the fact that I can tell you what any digit in the googolplex is (the first is a 1, the rest are all 0), no person, no computer, no civilisation will ever be able to write it out in full. This is because there is not enough room in the Universe to write down all googol+1 digits of a googolplex. As Kasner, and his colleague James Newman, said of the googolplex (in their wonderful 1940s book Mathematics and the imagination which introduced the world to these numbers): "You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way."
Graham's number is bigger than the googolplex. It's so big, the Universe does not contain enough stuff on which to write its digits: it's literally too big to write. But this number is finite, it's also an whole number, and despite it being so mind-bogglingly huge we know it is divisible by 3 and ends in a 7.
A big party
The origins of Graham's number go back to 1928 when a brilliant young mathematician, Frank Ramsey, noticed a surprising thing when he was working on a paper about logic: complete disorder seemed to be impossible. No matter how complicated your system looks, pockets of order of any size are always guaranteed to be there if the system is large enough.
This result, which was just a small part of the particular paper he was working on, was the start of a whole new field of mathematics called Ramsey Theory. This area of maths is often explained with the example of a party. Suppose you're having a party and you want to make sure you invite a good mix of people and decide to keep track of who knows who. Suppose you draw a map of the relationships of all your friends, linking two people with a blue edge if they are friends and with a red edge if they are strangers. Then you might end up with something like this:
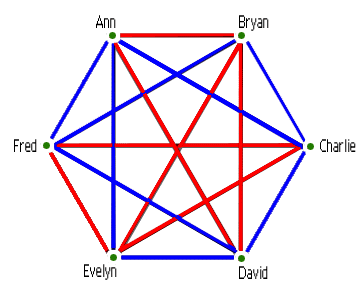
Now this looks pretty complicated and it would take quite a lot of information to describe who is connected by red edges and who is connected by blue edges. But if you zoom in on just Ann, Bryan and David, they are all joined by red edges. This red triangle is an example of order hiding in the messy overall network. The more ordered a system is, the simpler its description. The most ordered friendship network is one that has all the edges the same colour: that is, everyone is friends or everyone is strangers.
Ramsey discovered that no matter how much order you were looking for – whether it was three people who were all friends and strangers or twenty people who were all friends and strangers – you were guaranteed to find it as long as the system you were looking in was large enough. To guarantee yourself a group of three people who are all friends or all strangers you need a friendship network of six people: five people isn't enough as this counterexample shows.
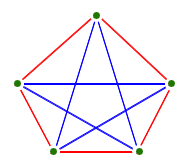
The number of people you need to guarantee that you'll find three friends or three strangers is called the Ramsey number R(3,3). We know a few Ramsey numbers: we've seen that R(3,3)=6, and it has been proved that R(4,4), the number of people you need to guarantee you'll find four friends or four strangers, is 18. But we hit a wall very quickly. For example we don't know what R(5,5) is. We know it's somewhere between 43 and 49 but that's as close as we can get for now.
Part of the problem is that numbers in Ramsey theory grow incredibly large very quickly. If we are looking at the relationships between three people, our network has just three edges and there are a reasonable 23 possible ways of colouring the network. For four people there are six edges and 26=64 possible colourings. But for the relationships between six people there are fifteen edges and we already have to consider an unwieldy 215=32,768 possible colourings. Mathematicians are fairly certain that R(5,5) is equal to 43 but haven't found a way to prove it. One option would be to check all the possible colourings for a network of 43 people. But each of these has 903 edges, so you'd have to check through all of the 2903 possible colourings – more colourings than there are atoms in the observable Universe!
Too big to write but not too big for Graham
Big numbers have always been a part of Ramsey theory but in 1971 mathematician Ronald Graham came up with a number that dwarfed all before it. He established an upper bound for a problem in the area that was, at the time, the biggest explicitly defined number ever published. Rather than drawing networks of the relationships between people on a flat piece of paper as we have done so far, Graham was interested in networks in which the people were sitting on the corners of a cube.
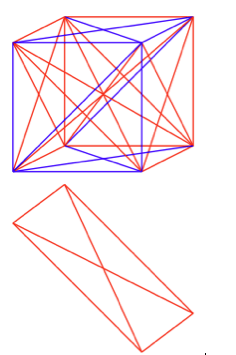
In this picture we can see that for a particular flat diagonal slice through the cube, one that contains four of the corners, all of the edges are red. But not all colourings of a three-dimensional cubes have such a single-coloured slice. Luckily, though, mathematicians also have a way of thinking of higher dimensional cubes. The higher the dimension, the more corners there are: a three-dimensional cube has 8 corners, a four-dimensional cube has 16 corners, a five-dimensional cube has 32 corners and so on. Graham wanted to know how big the dimension of the cube had to be to guarantee that a single-coloured slice exists.

Ronald Graham who gave us his beautiful number. Image: Cheryl Graham.
Graham managed to find a number that guaranteed such a slice existed for a cube of that dimension. But this number, as we mentioned earlier, was absolutely massive, so big it is too big to write within the observable Universe. Graham was, however, able to explicitly define this number using an ingenious notation called up-arrow notation that extends our common arithmetic operations of addition, multiplication and exponentiation.
We can think of multiplication as repeated addition:
3 x 3 = 3+3+3
33 = 3 x 3 x 3.
If we define the single arrow operation, ↑, to be exponentiation, so:
3↑3 = 33 = 3 x 3 x 3 = 27,
then we can define the double-arrow operation ↑↑ to be
3↑↑3 = 3↑3↑3 = 333 = 327 = 7,625,597,484,987.
We can carry on building new operations by repeating previous ones. The next would be the triple-arrow
3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑↑3)=3↑↑7,625,597,484,987
a tower of powers of 3 that is 7,625,597,484,987 levels high! (See here to read about the up-arrow notation in more detail.)
The number that has come to be known as Graham's number (not the exact number that appeared in his initial paper, it is a slightly larger and slightly easier to define number that he explained to Martin Gardner shortly afterwards) is defined by using this up-arrow notation, in a cumulative process that creates power towers of threes that quickly spiral beyond any magnitudes we can imagine.
But the thing that we love about Graham's number is that this unimaginably large quantity isn't some theoretical concept: it's an exact number. We know it's a whole number, in fact it's easy to see this number is a multiple of three because of the way it is defined as a tower of powers of three. And mathematicians have learnt a lot about the processes used to define Graham's number, including the fact that once a power tower is tall enough the right-most decimal digits will eventually remain the same, no matter how matter how many more levels you add to your tower of powers. Graham's number may be too big to write, but we know it ends in seven. Mathematics has the power not only to define the unimaginable but to investigate it too.
About this article

Rachel Thomas and Marianne Freiberger are the editors of Plus. This article is an edited extract from their new book Numericon: A journey through the hidden lives of numbers.
Comments
Michael Ossipoff
I'd like to answer to questions:
1. Question: How is Graham's number gotten from the Knuth up-arrow notationi?
Answer: As someone mentioned, here is what Graham's notation means:
(I'm using ^ to mean up-arrow. For exponentiation, ^ and up-arrow mean the same thing.)
g(1) is defined as 3^^^^3
g(n) is defined as 3^^^...^^^3 ...where the number of ^'s written is equal to g(n-1)
That g(n) function increases _very_ rapidly, as n increases.
Graham's number is g(64).
2. Question: What font-size is assumed when it's said that the observable universe isn't big enough to write Graham's number?
Answer: Writing Graham's number as a 1 followed by zeros, suppose you could write one of the zeros in every Planck volume in the observable universe. There aren't enough of them to write it.
If, instead of 1 followed by a string of zeros, you wrote "A trillion trillion trillion...trillion trillion trillion. ...with a long enough string of "trillion" to write Graham's number you'd still need 2/3 as many characters, and so it would still be impossible to write all that string of "trillion", by writing one character in of the Planck volumes in the observable universe,
How small is a Planck volume? It's a hundredth of a millionth of a trillionth of the volume of a proton.
In fact, not only could you not write Graham's number by writing a zero or or a letter of "trillion" in every Planck volume in the universe. It's said that you couldn't even write the number of digits in the number of digits,
...or the number of digits in the number of digits in the number of digits.
...and so on, repeating that number-of-digits thing as many times as the number of Planck volumes in the observable universe.
I'm just quoting something said at Wikipedia. I can't personally guarantee it.
But I can guarantee the first claim: You can't write the Graham number even if you could write a zero, or a letter in "trillion" in each Plank volume of the observable universe,
But that's achievable by much smaller numbers that Graham's number.
How many orders can 200 objects be arranged in? The number is greater than the number of Planck volumes in the universe,
Say you numbered and listed all those orders. How many orders could that list be arranged in? The number of orders for that would be too big to be written even if you could write a zero or a letter of the word "trillion" in every Planck volume in the observable universe
You know that scan-pattern called the QR code, that accesses an advertiser's website? At least one kind of QR code scan pattern uses a 35X35 square pattern of smaller squares
How many combinations of shaded and unshaded squares are there?
There are more than the number of Planck volumes in the observable universe.
In how many orders could the world's human population be arranged? About 10 to the power of 72 billion.
In how many orders could you arrange a number of objects equal to 10 to the 72 billionth power?
That number of orders is about the 400 millionth power of the number of Planck volumes in the observable universe.
Graham's number is incomparably larger than any of these numbers, But those order-numbers can be gotten in a familiar way, ordering a certain number of objects, And it doesn't take many objects (about 200) to have more orders than the number of Planck volumes in the observable universe.
Ravindra Singh
"Universe itself isn't large enough to write down Graham's number" This statement hold true irrespective the font size you use.
Iconoclast24601
Graham's number is so large compared to the size of the universe that the font size actually becomes irrelevant; whether one character takes up a Planck volume or the entire universe barely makes a difference.
Prof. Gonzo
Given that we are talking about filling the entire universe with numbers, extremely small numbers, it's not unreasonable, at least not more unreasonable, that we can consider that this 'font' we are talking about has zero thickness and as such there is more than enough space to write any number on the head of a pin.
Zach
I don't think thickness would matter you'd still have any 2 pieces of information you're using to describe each digit that are closer than a plank apart collapsing into black holes. I think that's what the plank scale is about - I could be wrong - wether separate things can have a meaningful distance apart regardless of their size, without just collapsing into a black hole. I think most quantum objects like electrons, etc. are described as having zero dimensions in every direction, un-intuitively dimensionless points, I think that's how someone who knew what they were talking about described it, don't quote me, and-I think-they were saying the plank scale was more about their distances from each other, and wether they are far enough apart to interact as expected or if they'll be too close and form a BH. Someone else here might know better.
Nic Barry
If the font size was 1/grahams number, I'm sure we could squeeze it in there. That's the only use for Graham's number that seems practical anyway.
mark schnitzer
1/grahams number would be vastly smaller than a Planck length, which is supposedly the shortest/smallest distance that has any meaning (about 10^-20 the size of a proton), so I guess font size couldn't be less than 1 Planck length. And there aren't anywhere near enough Planck units in the entire universe (around 10^186) to make a scratch on grahams number.
But if grahams number is that big, imagine what grahams number raised to the power of grahams number might be?? Then imagine this - there are still an INFINITY of numbers even larger than that!
anonymous
try this: graham's number^^^^^grahams number. these things get big... fast.
Ashton
Or you could use a operation of my own design it’s kinda like a hyperoperation but I haven’t seen it officially listed anywhere.
Basically F(n) whatever n is equal to tells you the number of operations used and the level of the last operation you’ll use that step. Ex
F(0)=0
F(1)=1+1=2
F(2)=2•(2+2)
F(3)=3^(3•(3+3))
F(4)=4^^(4^(4•(4+4)))
F(5)= 5^^}(5^^(5^(5•(5+5)))){^^5
basically in that last one there are approximately 5^^85decillion arrows with 5s on either end it’s kinda hard to notate on the phone but it’s already starting to stack in the same way Graham’s Number (G64) does by increasing the actual ammount of arrows. However, it should surpass Graham’s number a good while before F(64) I would imagine and so F(G64) would be absolutely humongous. I built this operation trying to create a fun pattern that would at some point outpace the TREE(n) function but I’ll never be certain if it would work or just how long it would take to grow faster cause TREE(3) is already so massively huge the gap is a VERY difficult one to breach. Like imagine how small 100 is next to G64 and TREE(3) makes G64 look beyond tiny I don’t even fully understand how.
also fun fact I tried calculating this pattern in reverse as well and kinda kept breaking things giving me the following answers before things really stop making any sense at all but it’s still fun to break the rules sometimes just to see what would happen if you could lol
F(-1)=0
F(-2)~ Infinity?
F(-3)~ (i)
F(-4)= DEFINITELY UNDEFINED
Chris Rapson
Firstly, that's an odd use of the term 'reverse' when talking about mathematical functions. At any rate, your table of values doesn't even follow from your definition of the function F.
To get F(-1) = 0, I presume you decided to 'invert' the operator, which would make F(-2) = (-2) ÷ [(-2) - (-2)] = -2 ÷ 0, which is undefined (not infinity). Since all subsequent terms will end with a (-x) - (-x) in a denominator, they are ALL undefined.
That being said, I think you have the beginning of an intriguing idea: the *down* arrow for repeated division.
Tim
Or... you could just use the up arrow and a minus number in the same manner that you do with normal exponents.
A down arrow would make more sense for roots
Anonymous
Could we write the number in digital form, which from my understanding would incredibly expand the number of digits that could possibly be written, or am I mistaken?
Anonymous
You're forgetting about the fact that if you consider our universe as a good example of space then you have forgotten that our universe is much smaller than, THE INFINITE AMOUNT of universes in space. Space is believed to be just a vacuum of stars and planets that are grouped together, and that these groups of groups of planets go on seemingly forever. So why are you fighting about fitting it in our universe. When if you tried, you wouldn't actually know when you've reached the outer reaches of our universe. You'd die before you could ever even attempt to record it. So let me put it to you like this, you're fighting about fitting that number into a place that could quite possibly have more universes in it than any number in the known universe could ever come close to being. Think about it like this, it's pretty much like fighting to put a number that can be used to explain how many universes our in existence. There's probably more than a g^g amount of universes in existence so why are you fighting about it, when you couldn't tell if you were in our universe or the one that's two universes over. It's a pointless argument. You're fighting about fitting something that is pretty much infinite into a space that is pretty much infinite. It's like fighting to fit infinity into infinity.
That Guy
What you're missing here is that a lot of the time (as in this case) when people say "the Universe" what they really mean is "The OBSERVABLE Universe", which is a VERY large but definitely finite size (about 93 billion light years). It is defined by the distance that light has had time to reach us since the beginning of the universe. https://en.wikipedia.org/wiki/Observable_universe
So you may be right about how large the universe outside of that area could be (which is unknowable, since it can literally never be observed) but it's not really relevant in this context.
Jeff Guarino
The proposed other universes are unreachable , and only conjectured. They are moving away from us at the speed of light or greater and no communication can happen. So they effectively don't exist. Unless we find new physics. So we are back to the case of countability and what are numbers. Numbers represent counting, when you talk about a number you need a way to define it and the Graham number gives a definition but can you really carry out this definition in real time in the universe. If you can't do that then you might as well talk about fairies. This is why there is no such thing as zero. You can never have zero of anything because quantum mechanics has the uncertainty principle. You can never pin down the location of anything with 100% precision. So you are counting apples that you pick from a tree and put in a basket. You put the first one in the basket but you don't know for sure that it is ever in the basket with 100 % confidence because there is a non zero probability that it is not in the basket. It is very low but not zero. So how do you get to zero ? It is simply not possible a 1/0 = infinity , so infinity is not possible either.
Unknown
If graham's number won't fit the whole universe, then how can that fit???
Also, what about; Graham's number^^^^^^^Graham's number is or even more... I feel like breaking apart, I cna't understand this type of stuff. (I'm just in 8th grade)
Crackers
Yeah the entire concept of how font size might relate to Planck volumes is pretty funny to me. It’s not possible in any way, so people getting caught up on the semantics is just funny. Like, if you can write the letters in “trillion” at a size where one letter is the size of one Planck volume, then you’re already somehow etching lines that are smaller than a Planck. In Wit hout higher-than-Planck resolution you wouldn’t be able to write any fonts at that scale. It would be like trying to write on grains of rice with a pen tip larger than a grain of rice. Easy to make a mark, difficult to write characters.
I think the metaphor about how big it would be if you wrote it out isn’t about maximizing font density, but rather about trying to put it into some kind of terms that people might understand relative to their daily lives. The formulation I first came across was based loosely on the number of characters that fits in an average book. This gives you a mechanism for imagining the data as a stack of books. So, if it were actually written out, not at a Planck scale, but a human scale, it would be about so big. This ”hardcover” model doesn’t work so well for super huge numbers because it’s just way more matter than we think exists. It does not make it easier to comprehend.
But you could imagine this “printed mass” might be an interesting way to envision some number or dataset, if it was say, the mass of the moon, or I dunno, an elephant.
True
Also true the font matters (as explained two times) for example if each millimeter was a zero (and one of the millimeters is a one) then I would guess that the number is bigger that Graham’s Number
Chris Rapson
Um...no. That's not even close to Graham's Number. Sorry.
Anonymous
Grahams number is bigger than googolplex, but is it bigger than googolplexian? (1 followed by googolplex zeros)
Adam Moran
Grahams number is so big, it makes the googolplexian look like a quark (something that makes another something and quarks are smaller than an atom.) :P
Adam Moran
Yes it is bigger it makes googolplexian look like the smallest thing smaller than the smallest thing and makes Grahams number look as big as the BOX that is the largest thing POSSIBLE!
blue ermine
Is it even possible to make a number bigger than grahms number?
Random Person
G(G)
Easy.
Tommy Johansson
.... But why that big, why does we know that the solution will be that number or smaller?
Is it a guess from Grahams part or is there a reasoning to go that far? I never seen that explained. Only that G1 is 3 4*arrow 3 and that is the number of arrows between the 3's in G2 and so forth until G64 why not just stop at G1 or why not continue to G1.000.000?
PaulMurrayCbr
Not sure if true, but IIRC: perhaps the best thing about Graham's number is that this absurdly massive number is an upper bound to the solution, and it's believed that the actual answer to the question is six.
Anonymous
You're forgetting about the fact that if you consider our universe as a good example of space then you have forgotten that our universe is much smaller than, THE INFINITE AMOUNT of universes in space. Space is believed to be just a vacuum of stars and planets that are grouped together, and that these groups of groups of planets go on seemingly forever. So why are you fighting about fitting it in our universe. When if you tried, you wouldn't actually know when you've reached the outer reaches of our universe. You'd die before you could ever even attempt to record it. So let me put it to you like this, you're fighting about fitting that number into a place that could quite possibly have more universes in it than any number in the known universe could ever come close to being. Think about it like this, it's pretty much like fighting to put a number that can be used to explain how many universes our in existence. There's probably more than a g^g amount of universes in existence so why are you fighting about it, when you couldn't tell if you were in our universe or the one that's two universes over. It's a pointless argument. You're fighting about fitting something that is pretty much infinite into a space that is pretty much infinite. It's like fighting to fit infinity into infinity.
Anonymous
What you're missing here is that a lot of the time (as in this case) when people say "the Universe" what they really mean is "The OBSERVABLE Universe", which is a VERY large but definitely finite size (about 93 billion light years). It is defined by the distance that light has had time to reach us since the beginning of the universe. https://en.wikipedia.org/wiki/Observable_universe
So you may be right about how large the universe outside of that area could be, but it's not really relevant.
Anonymous
I'm not a mathematician - far from it. Every time I come back to Graham's number I can't get my head around Knuth's up-arrow notation. I interpreted it in my own way, but I have a feeling I've got it wrong. The way I thought of it is that:
Step 1: 3^3 = 27. Take that result (27) and make it the new power:
Step 2: 3^27 = 7.6 trillion. Take that result (7.6T) and make it the new power:
Step 3: 3^7.6T = ? (An "Impossibly Huge Number.") Take that result (I.H.N) and make it the new power:
Step 4: 3^I.H.N = ? (A "Savagely Huge Number.") Take that result (S.H.N) and make it the new power:
Step 5: 3^S.H.N = ? And so on, and so on. (I forget which one would be "G1", step 4 or step 5 maybe)
- What I'd like to know is whether this way of looking at it is right or not. Obviously you can't write anything down without coming up with "Magnificently Ridiculous Names" for these numbers so it defeats the object, but I'm trying to get my head around the process.
Thanks in advance for any help, I really appreciate it.
Chris Rapson
You actually are interpreting the arrows quasi-correctly.
Step 1: 3^3
Step 2: 3^^3 = 3^27 = 7.6T
Step 3: 3^(3^^3) = 3^3^3^3 = 3^^4
Step 4: 3^(3^^4) = 3^^5
The tricky part to wrap your head around is the addition of a third arrow.
New Step 3: 3^^^3 = 3^^(7.6T) which means repeating your original version of Steps 4, 5, 6, etc. all the way to Step 7.6T! Then you would have to add yet *another* arrow, which means you have to take the result of that Step #7.6T and continue repeating your steps to reach *that* step number. Then, FINALLY, you would have G1.
Brain broken yet?
Jeff Guarino
Numbers come from counting. If you can't physically count to the number than it doesn't exist. Counting is just a short hand for grouping things into a location. For example I pick apples from a tree and place them in a basket. The number of apples remains the same but I am defining my counting by only the apples in the basket. So the short hand of multiplication and exponents etc. represent the physical act of counting things one at a time but is just a short hand. If you can't actually count to a number than it doesn't exist in the physical universe. You need things to count and there are only so many atoms or particle to count and then you have to have a method of grouping the things you are counting. So it involves physics. Quantum physics, time , gravity etc. Why is this number considered to be the largest ?? You have a way of defining Grahams number but carrying out the definition is in itself impossible. This is why infinity is impossible and infinity + 1 is impossible also. When you count and attempt to count higher than anyone or anything has ever counted to before you will eventually reach a number and if you try to add 1 to this number you will fail. Something physical will prevent you from counting higher.
TheMiner1501
The great thing about mathematics is that it's unbound by reality. We don't need physical things to count. It may have started that way but it's evolved way past that. Mathematics is not defined by physics, mathematics is a study in and of itself.
Chris Rapson
"Why is this number considered to be the largest ??"
This is the largest NAMED number. Obviously, there are an infinite amount of numbers larger.
Even if our use of the concept of numbers began with counting, mathematics (which encompasses not only numbers but the relationships between abstract quantities like time and gravity) is a language. It's the language of our reality. In English, we can certainly use words to express concepts that don't physically exist in our Universe, and we can describe imaginary objects that don't (or even can't) exist physically. By your logic, the following words wouldn't exist for me to write: the orange-colored Beaver Queen of donuts.
Math is no different. It's a language fully equipped to describe any numerical concept, whether or not it could exist in our Universe.
Cara
Leen
It's fun to toy with big numbers, but all this iterated power stuff is primitive recursive. All primitive recursive functions are dwarfed by Ackermann's function for relatively small arguments, whereas the Ackermann function itself is in turn dwarfed by the Busy Beaver function.
Richard Catterall
I was wondering when someone would mention Ackermann's function. Imagine Ack(Graham's number)!
Anonymous
g(Graham’s number)
Mike Oxlong
Graham’s Number plus 1?
danR^^3
I imagine that an encryption scheme incorporating g64 would be well-nigh unbreakable.
lynn lines
When it comes to encryption u should be aware that as of now (june 2020) advances in quantum computing have made encryption a thing of the past, in fact a 512 qubit computer could anylise every known atom in the universe in less than a second!. But when it comes to maths we are approaching an entirely new and unknown area, the more we learn the more we are starting to realise that numbers are not a unit of measurement or way of defining amounts but more like a system of programming that exist everywhere and are undeniably fundemantal to not just the field of mathematics but life itself..you have golden ratios and fibonacci sequences...etc...etc... which the more i have researched the more weird things start to get...grahams number, googleplexians are all well and good but the current field of quantum physics is on the cusp of rendering everything we know and believe to be absolutely incorrect....watch this space...
anonymous
grahams number is g64
g's will be 1 layer of grahams
p will be one layer of googol/googolplex/googolplexian
starrting from a level playing field (0)
how long will the exponential increase of grahams take to catch up to p's expansion
one layer of g increases it by a power of 3
one layer of p increases it by a power of 10
meaning that 3 layers of g is equal to 1 layer of p
googolplexian = ~g9
Ian
No, each layer of Graham doesn't raise to the power of 3 or you could easily write g64 as a power tower. It raises the order of the operation by g(n-1). Exponentiation can't ever beat it, that's just a single arrow.
Holly Mccormack
Graham’s number plus one. I win.
Oscar
My own maths thing I(x) is B I G
I(x) = x^x^x and so on x+1 times
I(0)=0
I(1)=1^1=1
I(2)=2^2^2=2^4=16
I(3)=3^3^3^3=3^3^27=3^7625597484982=a number with over 36 TRILLION DIGITS
I(x) where x is Bigger than 3 is in computable
I(0.5)=0.25
I(1.5)=1.5^0.75≈1.3554
Bye!
Stairs
So having read all the comments on how this works, would I be right in saying that Graham's number is
"
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^(3^3^7625597484987)^
"?
I used the information on g1 supplied by "The epic boss" to get the first part and then multiplied it by 3^^^^3 to get g2, and then by it again to get g3 and so on to get g64 which was supposed to be Graham's number. I was just interested to see how it would be written out in numerical terms rather than algebraic (which may not be possible in full as it is more than the number of atoms in the universe) but to write it in its shorter version using the up arrow operation.
Thanks
blue ermine
this number is both amazing and ridiculously confusing. Is there any bigger number known?
kale g
googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex^googolplex
Melissa Hunter
My 7 yr old loves learning about Goggolplex and Graham’s number and all the big numbers. Is there anything you could recommend to give him to encourage this love of maths.
._.
Your 7 yr old is learning Googolplex and Graham’s number?!?! wow, you have a smart kid.
Sir Da Nerd
Graham’s number may be big, bit is it bigger than The Marioplex, the amount of possible levels in Super Mario Maker 2, a number so large that the amount of atoms in the observable universe is dwarfed in comparison?