
Understanding uncertainty: What was the probability of Obama winning?
On the face of it this seems an odd question. After all, he’s won. But before the election it was uncertain whether Obama would win, and probability is how we quantify uncertainty. So what can we say about how this probability should have been assessed?
The bookie's view
We know that there were betting odds — a betting exchange such as Intrade allows people both to accept or make bets. The process converges, at any point in time, to a certain set of odds at which people are willing to be either the better or the bookmaker. This prediction market provides a "probability" of Obama winning the election. This probability kept changing over the year before the election, as shown in figure 1 with some of the main events of the year marked in.
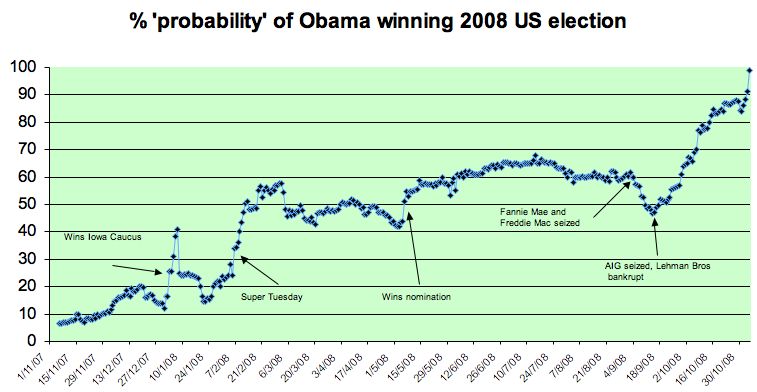
We can see how the betting odds changed in response to events. Before getting the nomination by the Democratic party, Obama had to compete with other candidates, primarily Hillary Clinton, in each state. In the early stages of the campaign Clinton was the firm favourite, although the probability of an Obama victory briefly touched 40% after he won important states. His odds went above 50:50 in February after more successes against Clinton, and rose again when Clinton admitted defeat in May. His main competitor now was McCain, and Obama stayed the favourite until the financial crisis became very dramatic in September. From the government take-over of the major mortgage organisations through to the failure of the Lehman Brothers bank and the AIG insurance company on the 15th of September, Obama's odds fell steadily until McCain was briefly the favourite. However, from the 15th of September the odds on Obama steadily increased until election day on November the 4th.
In this context a "probability" of 20% means that people were willing to take and make bets at 4 to 1 against, which means that if someone put £1 on Obama winning, they would receive back £4 winnings plus their stake to make £5 in total. (I don't usually gamble, but in January 2008 I did place an online bet of £1 on Obama at 4 to 1 odds, in the middle of a lecture to a post-graduate class in Cambridge, in order to illustrate how odds transform to probabilities: this choice was treated with some derision at the time. Gambling during a lecture probably also broke some medieval statute of the University!).

Made it! But what were his chances of getting here?
But do these betting odds really represent the probability? How does this fit with how probability is taught in school? In fact, what does probability mean? Does it even exist? These are reasonable questions to ask, and we quickly get into tricky philosophical issues. Let's look at the different ways we might think about probability, and whether each way might tell us what the probability of Obama winning might have been.
Perfect symmetry
The classical idea of probability is based on equally likely outcomes: if there are $N$ possible outcomes, the probability of each one occurring is is $1/N$. This is what is generally taught in schools, and works fine for coins, dice and other physical objects where it may be reasonable to assume some symmetry between the outcomes. In the election there were two main candidates, so would the probability of Obama winning have been 50\%? The mere fact that there are two alternatives does not imply that these are equally likely. And in fact there were up to 14 other candidates including names that could be written in, depending on the state, but a probability of 1/15 seems even more unreasonable. So the classical view does not work here.
How many times?
The frequency interpretation is based on the proportion of events with a particular outcome that occur in the long run: for example, we might say the probability of a dropped piece of toast landing butter-side down is 80% if that is the proportion of times it happens if we keep dropping toast (in controlled conditions) for millions of times. But this interpretation is difficult to apply to specific events, such as Obama becoming president, since they are essentially unique. We would need to place the event in a class of repeatable opportunities that stretch into the future, such as "black men becoming president". Looking into the past we note that there have been 43 presidents of the USA of whom precisely 0 have been black, so the current observed proportion is 0/43. Does this mean the best estimate of the probability that Obama becoming president was 0%? Clearly this would be ridiculous. Even if we were misguided enough to place Obama within this class of events, there is a better way of working out a probability, which will be explained below.
Parallel futures
Another possibility that has been suggested is that there is some true underlying "degree of belief" in the statement "Obama will be the next president" which, given the knowledge that we have, it would be logical to hold. This proposal leaves open the question of how to estimate this quantity and does not seem helpful in this situation.
Rather more attractive is the idea that there is some true underlying propensity for an event to happen — this is an objective state of the world, but needs to be estimated from what we know. One mental picture for this is to consider all the possible ways in which things might turn out, and then think of what proportion of these possible futures end up with Obama being President. This approach seems a bit shaky from a philosophical point of view (can we really think of the set of possible futures?), but means that we can think of probability as a frequency without having to think of some class into which to embed the event we are interested in.
A gambler's view

Parallel futures: Obama's rival Hillary Clinton, talking at Augsburg College two days before Super Tuesday. She's now been chosen as his Secretary of State. Image by Calebrw.
The final way of thinking of the probability of Obama winning the election comes back to betting: the probability is essentially the odds you are willing to accept in a bet based on your own subjective judgement. The betting exchange probabilities plotted above provide a kind of group assessment. Such probabilities could be interpreted as your best current estimate of the "true" probability (which is not directly measurable).
Alternatively we can say that the probability is not an estimate of any actual quantity in the outside world, but simply an assessment of the odds that you are willing to take (personally, this is the interpretation that I prefer). You don't have to actually place any bets: your probability that Obama will be president is, say, 50% if you are indifferent between the following two options: either (a) obtaining a reward if Obama becomes president, and (b) obtaining the same reward if a flipped coin comes up heads.
The attractive thing about this interpretation of probability is that it does not matter whether the event is truly unpredictable, or whether it is pre-ordained and you just don't happen to know how things will turn out. For example, before I flip a coin, you may say your odds are 50:50 on heads. If a flip the coin but cover up the result, your odds should not change, even though the uncertainty is now due to our ignorance rather than any essential unpredictability. If I then look at the coin but don't show you, then your probability should still be 50%, even though mine is either 0 or 100%.
This view says that probability does not exist, but is simply a numerical expression of your personal uncertainty, given the current information. Rather strangely, it means that probabilities can be quantified but not measured, rather like the value of things, be they a painting or a loaf of bread, does not objectively exist but depends on what people are willing to pay.
Laplace and the Sun

Laplace (1749-1827): calculated the chance of the Sun rising tomorrow.
So how can we assess probabilities in repeatable situations? Things are made easier if we see the current event as part of a sequence stretching back into the past and into the future, and we have no reason to think that any member of the sequence is systematically different from any other. We call the events exchangeable, and if we are willing to assume this (which we would not for Obama), there is a neat way of assessing the probability of the next event.
An Italian actuary called Bruno de Finetti showed that if we are willing to assume exchangeability, then things behave as if there were some "true" underlying chance for the event to happen, we just don't know what it is. In the long run the proportion of events that occur will tend to this underlying chance, which we will can $p$.
Suppose we have observed $n$ possibilities for an event to occur, and it has actually occurred in $r$ of them. What is the chance it will occur at the next opportunity? This is a classic problem, dealt with by the clergyman Thomas Bayes in a paper published in 1763 (when he had been dead for two years) and Pierre-Simon Laplace in 1814. Laplace provided the simple rule:
If before we observed any events we thought all values of $p$ were equally likely, then after observing $r$ events out of $n$ oportunities, we would assess the chance of the next event as $$p=\frac{r+1}{n+2}.$$
This is a major statement, and we should look at some examples. Before we start, $r=0$ and $n=0$, so Laplace's rule gives $p=\frac{1}{2}$ - when we claim entire ignorance, then our odds are 50:50. Suppose we then observe the event at the first opportunity: then $r=1$, $n=1$, and $p=\frac{2}{3}$. After the second event in succession, $r=2$, $n=2$ and $p=\frac{3}{4}$, and so on, so after 1,000,000 events occurred in 1,000,000 opportunities we have $p=\frac{1000001}{1000002}$. We note that $p$ never takes the value 1 (because $r$ is less than or equal to $n$), so we can never be completely sure that the event will happen next time. This is an example of Laplace's law of succession, which he applied to the question of whether the Sun will rise tomorrow. By working out how many days $n$ it had risen, we can say that the chance of it rising tomorrow is $\frac{n+1}{n+2}$. It seems that Laplace was rather mischievous in using this as an example, as he also pointed out:
But this number [the odds of the Sun coming up tomorrow] is far greater for him who, seeing in the totality of phenomena the principle regulating the days and seasons, realises that nothing at the present moment can arrest the course of it.
Which shows that applying his formula in an unthinking manner can be absurd.
For another application of Laplace's rule, suppose you are told that a bag contains a mixture of black and white balls, but you are not told the proportion of each. You draw out ten balls, putting each back after you have drawn it, and three of them are black. What is the chance that the next is black? Well, assuming that the balls are well-mixed, and that you thought before you started that all proportions were equally likely, then the chance is 4/12 = 1/3.
So now you know how to use past evidence to assess the chances of future events. Laplace's law of succession can be derived rigorously using integral calculus. However, you can only use past evidence to assess the chances of future events if you think that the future is going to carry on just like the past, and that can be a very dangerous assumption. If you want an example, think of the free-range turkey on Christmas Eve, happily looking forward to the next day of food and shelter, just as he's always known in the past.
About the author

David Spiegelhalter is Winton Professor of the Public Understanding of Risk at the University of Cambridge. David his team run a new website called Understanding uncertainty, which informs the public about all issues involving risk and uncertainty.