
What is a square?
What is a square? It's a shape that has four straight sides of equal length and four angles of 90 degrees.
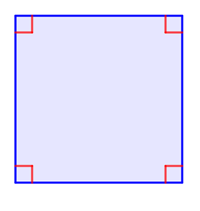
An honest square: it has four straight sides of equal length and four 90 degree angles
The 90 degrees and the four straight sides seem to go together. It's impossible to draw a triangle with all 90 degree angles. And it's similarly impossible to draw a pentagon, hexagon, or shape with more straight sides that has all 90 degree angles.
Or is it?
The two-dimensional, flat surface we usually do our geometry on at school is known as the Euclidean plane. It is true that on this plane, any closed, straight-sided figure whose sides are all the same length and whose interior angles are all right angles must have four sides — it must be a square. However, there are different types of surfaces which can be described using the notion of curvature. What happens if you change the curvature of the plane? Will the number of sides of the shape change?
How curvy is curvy?
You can measure how bent a surface is at a given point using the notion of Gaussian curvature (named after the mathematician Carl Friedrich Gauss). The details are explained in this article, but for our purpose we distinguish three types of surfaces: those that have zero Gaussian curvature at every point, those that have positive Gaussian curvature at every point, and those that have negative Gaussian curvature at every point.
The Euclidean plane has zero constant curvature at every point, as you'd probably expect: the plane isn't curvy, so it should have zero curvature. A sphere has positive Gaussian curvature at every point. Intuitively that's because it "curves outwards" in all directions. If you sat yourself down at any given point on the sphere, you'd see the sphere curving downwards away from your bottom in all directions.
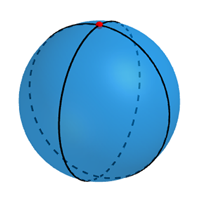
An sphere has positive curvature at every point. If you sat yourself down at a point, for example the red one in the figure, and looked down, you'd see the sphere curving downwards in all directions. Technically, the two black lines in the figure give the principal curvatures of the sphere at the point, which in this case are both positive. The Gaussian curvature is the product of the principal curvatures, which in this case is also positive. See this article to find out more.
Something very different would happen if you sat yourself down on a saddle shape, as if you were on a horse. If you looked down your legs, you'd see the surface curving downwards away from your bottom. But if you looked down right in front of you or right behind you, you'd see the surface curving upwards towards your head. This "opposite curving", intuitively, is what characterises negative curvature.
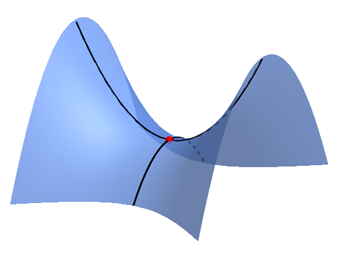
A saddle has negative curvature. If you sat yourself down at the red point and looked down your legs, you'd see the surface curving downwards. If you looked down right in front or behind you, you'd see the surface curving upwards. Technically, the two black lines in the figure give the principal curvatures of the saddle at the point. In this case one principal curvature is positive and the other negative. The Gaussian curvature is the product of the principal curvatures, which in this case is negative. See this article to find out more.
In general the Gaussian curvature could take different values at different points of a surface. Indeed, that is the case for the saddle above. What makes the sphere special is that the value of the Gaussian curvature is the same at all points: it has constant positive curvature. Another example of a surface that has constant Gaussian curvature is the pseudosphere, shown below. In this case the curvature is negative.
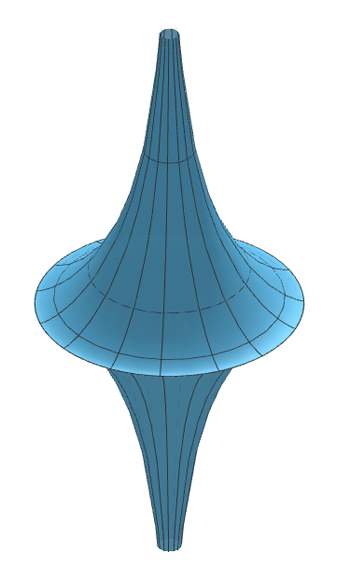
A piece of a pseudosphere, which has constant negative curvature. The actual pseudosphere continues indefinitely in both vertical directions. Technical note: The pseudosphere is a partial model of hyperbolic geometry.
Shapes on a sphere
So how many sides can shapes with straight sides and 90 degree angles between the sides have on these surfaces?
Let's start with a sphere and imagine it as having an equator and a North pole, just like the Earth. Start from a point on the equator and follow a line of longitude up to the North pole (such a line always forms a 90 degree angle with the equator). Now find another line of longitude that makes a 90 degree angle with the one you just walked up, and walk down that new line of longitude until you hit the equator again. Now walk along the equator until you reach your starting point.
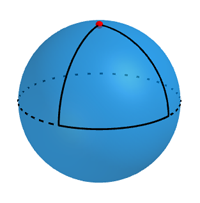
A spherical triangle with 90 degree angles and sides of equal length.
The lines you have walked along all form parts of great circles on the sphere, that is, circles that have the same diameter as the sphere itself. Each line corresponds to a quarter of a great circle, so they all have the same length. The great circles on a sphere are the analogues of straight lines on the plane. That's because, just like the shortest distance between two points on a plane is along a straight line, so the shortest distance between two points on a sphere is along a great circle. (In technical language, a line of shortest distance on a surface is called a geodesic)
What we have created here is a straight-sided shape whose sides all have the same length and meet in 90 degree angles — and it has three sides, not four! This also illustrates that the angles of a triangle drawn on a shape with positive curvature add up to more than 180 degrees (which is the case in the plane). In our example, they add up to 90+90+90=270 degrees.
On the sphere we can even draw a two-sided shape whose sides have the same length and meet at 90 degree angles. One side consist of half a great circle, and the other of one half of the great circle that's at right angles to the original one. Such a shape is called a digon.

Each of the four wedges cut out of the sphere by two perpendicular great circles is a digon.
Shapes on a pseudosphere
So, we have just seen that on a sphere (which has positive curvature) we can draw a shape with 90 degree angles and all sides the same length which has fewer than four sides. And it turns out that on the pseudosphere (which has negative curvature) we can draw such a shape with more than four sides. Below is an example with five sides.
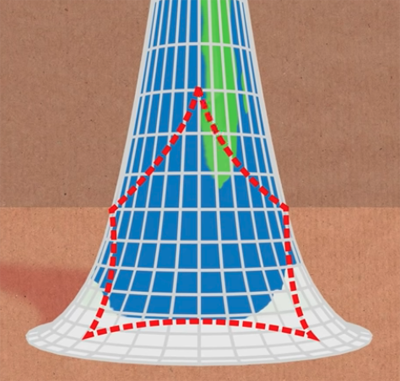
This five-sided shape drawn on the pseudosphere has straight sides of equal length and 90 degree angles. (We only show the top part of the pseudosphere here as it's sufficient for the illustration.) The image is taken from the Numberphile video 5-sided square, on which this article is based.
The angles here look smaller than 90 degrees, but this is an illusion caused by the negative curvature. In a similar way, the positive curvature of the sphere made the 90 angles in the triangle we saw above look bigger than 90 degrees.
Although the sides of the five-sided shape look curved to us, they are straight in the sense that they're segments of geodesics: lines of shortest distance on the pseudosphere. And as it turns out, they are all the same length.
So, if you thought that 90 degree angles and straight sides of the same length define a square, then think again. It all depends on the curvature!
Can you draw such shapes with six, seven, eight, or even more sides? We leave that up to you to find out.
About this article

Hannah Darken.
This article is based on the Numberphile video 5-sided square which you can see below.
Hannah Darken is a 19-year-old student from Liverpool. Hannah initially wrote this article while she was studying for her A-Levels at the University of Liverpool Maths School (ULMaS). She is currently in her first year reading mathematics at Lancaster University.
Comments
David Harold Chester
An accute-angled triangle has its vertices laying on three orthogonal axes. Where is there material about solving for the area of this triangle, when we know the distance from the origin of these intersection points?