Curves bring great beauty to our world. Curves are also a beautiful and important part of mathematics. Understanding curvature can shed light not just on beautiful shapes but can even reveal the undulations of spacetime itself.

Off on a tangent

If I ask you to think of a curve, you might think of a circle, a spiral, a sine wave, or some intricate curving squiggle. Almost certainly you won't think of a flat, straight line, and you won't think of a line of jagged spikes and sharp corners.

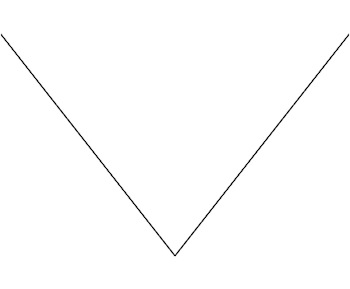
The graph of the absolute value function y=|x|

Really we are interested in curves that look smooth. Mathematically speaking we mean those that have a tangent to the curve at every point. For example, the graph of the the absolute value function, $y=|x|$, is the straight line $y=-x$ for negative values of $x$ and the straight line $y=x$ for positive values of $x$. As the graph is a straight line at any of these points, it is identical to its tangent there. But there is a problem at the point $x=0$, the sharp corner at the centre of the graph. Just to the left the graph has a slope of -1, and just to the right the slope is 1; the slope switches abruptly either side of $x=0$. It's impossible to define a tangent for a sharp corner and so the graph of $y=|x|$ is not a curve.

A parabola, the shape traced out by the arc of water from a fountain or the path of a ball thrown through the air, is a smooth curve. The function $y=x^2$ describes a parabola and has a tangent at every point in the curve (at any point $x=a$ the tangent is the line $y=2ax-a^2$). For large positive or negative values of $x$, far to the left or right of the centre of the parabola, the curve flattens and is very similar to its straight tangent line at these points. But as you get closer to the centre of the parabola the difference between the tangent and the curve becomes more and more obvious.

Intuitively, and mathematically, curvature is how far something, say a line or a surface, is from being flat. For any curved line, we can consider how different it is to its tangent at that point. Although a straight line is technically a curve, because it has a tangent at every point, it is a pretty boring one – this curve never differs from its tangent. But in our example of a parabola, the curvature changes depending on where you are on the curve. A parabola is most curvy, that is, it has the highest value of curvature, at the centre point, where it differs the most from its flat tangent. This is because at this point the direction of the tangent line changes the most quickly as you move along the curve: far out to the left or right of the centre the tangent only gradually changes direction as you move along the curve but close to the centre of the parabola the tangent changes direction much more rapidly. Mathematically, the curvature of a line in a flat plane is defined as the rate at which its tangent changes direction as you move along the curve at a constant speed. (You can find all the details of how to calculate the curvature, tangent and normal – the line perpendicular to the tangent – of a curve here.)

Kissing the curve

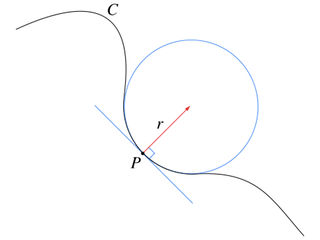
Another way of thinking about curvature is to approximate a curve at a particular point with a circle. This circle, called the osculating circle (meaning the "kissing circle") just touches (or "kisses") the curve at that point and has the same curvature as the curve there. The curvature of any circle is $1/R$ where $R$ is the radius. A circle with a very large radius has a very small curvature – walking in a straight line on the Earth is travelling round a giant circle but we don't really notice this curvature at all and it feels very much like walking on a flat surface – while a small circle with a tiny radius has a very large curvature. So the curvature of any point on a curve can be defined as $1/R$ where $R$ is the radius of the osculating circle at that point.

The final piece in the puzzle of curves in a plane is a matter of sides – which side of the tangent line does the curve lie on? The bit of a curve near where a tangent touches it can lie "above" the tangent line, or "below" it. If it lies below it, then the tangent line moves in a clockwise direction as you move from left to right along the curve. If it lies above it, like with our parabola above, then the tangent line moves in an anti-clockwise direction as you move from left to right along the curve. To distinguish between the two situation we can assign a positive value of curvature to points for which the bit of curve near the tangent lies below the tangent and a negative value to points where the bit of curve lies above it. Of course there are curves for which the value of the curvature switches from negative to positive and back again; an example is the sine wave below. It all depends on which points on the curve you are interested in.

Moving on up

We now have a clear picture of what curvature means for a curve drawn on a flat plane. We can use our knowledge of one-dimensional curves to help us understand the curvature of a two-dimensional surface. Here, again, curvature is all about how something differs from flat, but this time it is how the two-dimensional surface differs from its flat tangent plane.

To understand this we drop down to the one-dimensional curves we're already familiar with. For a point on the surface, consider all the planes that are perpendicular to the tangent plane and pass through the point (that is, they contain the normal to the surface at that point, where this time the normal is the line that is perpendicular to the tangent plane). Then the intersection of each plane with the surface is a one-dimensional curve and we can use our methods from above to calculate the curvature of these one-dimensional slices at this particular point. The maximum and minimum curvatures of these sliced curves are called the principal curvatures, $\kappa_1$ and $\kappa_2$. The Gaussian curvature of the surface at a given point is just the product of the principal curvatures. The surface has positive curvature (called locally convex) if $\kappa_1 \kappa_2 >0$. This means that the surface stays on the same side of the tangent plane near this point. If the surface has negative curvature, that is $\kappa_1 \kappa_2 0$, the surface is saddle shaped.

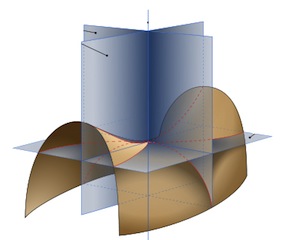
Although Gaussian curvature is defined in terms of intersecting planes, Gauss showed, in his Theorema Egregium or "remarkable theorem", that this is an intrinsic invariant of the surface. The intrinsic nature can be understood in terms of tiny two-dimensional resident living on the surface: they would be able to detect the positive, negative or flat curvature of the surface by summing the interior angles of triangles: they will detect a positive curvature if the interior angles add to more than 180° (such as on the surface of the Earth), a negative curvature if the interior angles add to less (a surface similar to that of a crinkly kale leaf) and if they add to exactly 180° it is a flat surface with a curvature of 0.

So curvature, whether you live in two dimensions or three, is just a matter of kissing circles and tangents. But what happens if you live in four dimensions, or more? Find out in the next article.

About the author

Rachel Thomas is Editor of Plus. Rachel would like to thank Graeme Segal for all his help and patience in explaining mathematical curvature.