
The power of origami

Allosaurus skeleton made by Robert J. Lang from 16 uncut squares of Wyndstone 'Marble' paper. Size: 24 inches. Image courtesy Robert J. Lang.
When I was nine I was an origami master. I had a friend called Kim, who was visiting England for a year from Japan. While I showed Kim some of the fun things to do in England, she taught me all sorts of cool Japanese things, from drawing Manga cartoons to making sushi. Of course, another thing she taught me was origami — and one afternoon she taught me how to make a paper crane. From that moment on, I was the greatest origami master in the world. Or so I thought. It was another fifteen years before I realised that I wasn't, and in fact never had been anything close to an origami master.
Surprisingly, I wasn't the only one to have made this mistake. There were undoubtedly many artists throughout history who genuinely believed that they had produced the best, most complicated origami models possible. In fact, it wasn't until well into the 20th century, with the rise of computers, that origami really took off.
A short history of Origami
Although origami is nowadays synonymous with Japan, the first recorded reference to it comes from China, where paper was first produced around 200AD as a cheap alternative to silk. The art of Chinese paper folding was known as Zhezhi and was brought with paper to Japan in the 6th century by Chinese Buddhist monks.

Pegasus made by Robert J. Lang from one uncut square of Korean hanji paper. Size: 7 inches. Image courtesy Robert J. Lang.
Origami took off in Japan from then onwards. The Japanese word "origami" itself is a compound of two smaller Japanese words: "ori", meaning fold, and "gami", meaning paper, and the art was (and still is) a popular pastime for Japanese children for many centuries.
And so it may have remained, were it not for a Japanese factory worker called Akira Yoshizawa, who was born in 1911 to the family of a dairy farmer. Akira took pleasure in origami when he was a child, and like most children, he gradually stopped as he grew older and found new things to occupy his time. However, unlike most children, he re-kindled his relationship with origami when he was in his early 20s. He had taken a job in a factory, teaching junior employees geometry, and he realised that origami would be a simple and effective way of teaching his students about angles, lines and shapes.
As Yoshizawa practiced more and more, he developed some pioneering techniques such as "wet folding", which allowed much more intricate patterns and even curves to be formed out of a single sheet of paper. His work launched an origami renaissance, with his new techniques turning origami from an oddity into an art form. As more and more complex origami patterns were designed, the art began to receive interest from mathematicians, who had the same idea as Yoshizawa — there was a huge cross-over between paper-folding and geometry. The mathematical study of origami eventually led to a new approach to two problems that had their roots in a different culture, on a different continent, many, many years earlier.
Euclid's elements
Euclid of Alexandria was a Greek mathematician who lived over 2000 years ago, and is often called the father of geometry. Euclid's book The Elements is the most successful textbook in the history of mathematics, and the earliest known systematic discussion of geometry.
Euclid knew that by using a straight-edge and compass (a straight-edge is like a ruler without markings), it was possible to perform a large number of geometric operations, like drawing a pentagon, a hexagon and a circle. This was widely known at the time, and Euclid being able to do this was by no means unusual.
However, what Euclid did that no-one else had done before, was to take a systematic approach to geometry. Every geometric construction and every mathematical result in The Elements was derived step-by-step from a set of five assumptions, which include the basic operations that are possible with straight-edge and compass:
- Given any two points, one can draw a straight line between them;
- Any line segment can be extended indefinitely;
- Given a point and a line segment starting at the point, one can describe a circle with the given point as its centre and the given line segment as its radius;
- All right angles are equal to each other;
- Given a line and a point P that is not on the line, there is one and only one line through P that never meets the original line.

Hummingbird & trumpet vine made from multiple sheets of Korean hanji paper, wire, and wood. Size: 15 inches. Image courtesy Robert J. Lang.
The assumptions, known as Euclid's axioms, seem obvious, and indeed Euclid himself presumed them to be so obvious as to be self-evident. But their beauty lies in the fact that they can be used to construct geometric proofs of theorems that are immensely more complex than the axioms themselves.
But there are also limitations to Euclidean geometry. Two of the most famous problems of antiquity were the trisection of the angle (dividing a given angle into three equal parts) and the doubling of the cube (constructing a cube which has exactly twice the volume of a given cube). According to legend, the citizens of ancient Delos were faced with the latter problem when the oracle at Delphi advised them to double the volume of their altar, in order to avert the plague. This, however, proved impossible using only Euclid's straight-edge and compass methods, and the same goes for angle trisection. But it turns out that both problems can be solved using origami! So we are left with the astounding possibility that origami geometry is more powerful than Euclidean geometry.
The genius of origami
Just as Euclid devised axioms for planar geometry, the modern mathematicians Humiaki Huzita and Koshiro Hatori devised a complete set of axioms to describe origami geometry — the Huzita–Hatori axioms (click here to skip the axioms and see the rest of the article):
| Axiom 1: Given two points $p_1$ and $p_2$, there is a unique fold that passes through both of them. |
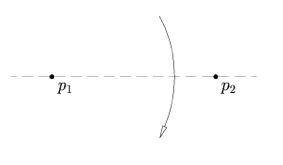 |
| Axiom 2: Given two points $p_1$ and $p_2$, there is a unique fold that places $p_1$ onto $p_2$. |
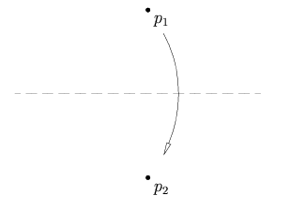 |
| Axiom 3: Given two lines $l_1$ and $l_2$, there is a fold that places $l_1$ onto $l_2$. \;\;\;\;\;\;\;\; |
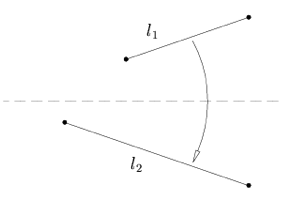 |
| Axiom 4: Given a point $p_1$ and a line $l_1$, there is a unique fold perpendicular to $l_1$ that passes through point $p_1$. |
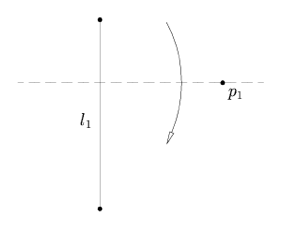 |
| Axiom 5: Given two points $p_1$ and $p_2$ and a line $l_1$, there is a fold that places $p_1$ onto $l_1$ and passes through $p_2$. |
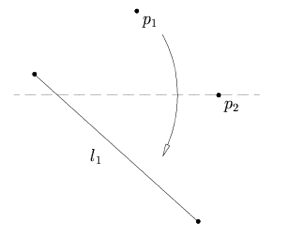 |
| Axiom 6: Given two points $p_1$ and $p_2$ and two lines $l_1$ and $l_2$, there is a fold that places $p_1$ onto $l_1$ and $p_2$ onto $l_2$. |
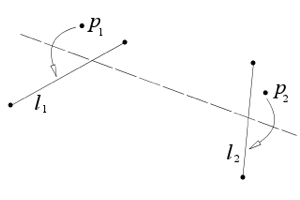 |
| Axiom 7: Given one point $p$ and two lines $l_1$ and $l_2$, there is a fold that places $p$ onto $l_1$ and is perpendicular to $l_2$. |
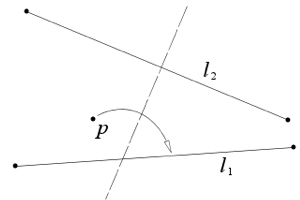 |
Trisecting the angle
The seventh axiom is the key to both trisecting an angle and doubling the cube. Let's start with the angle construction. By following the steps outlined below, it is possible to see how these simple axioms can enable the folder to perform an operation which eluded Euclid. (Diagrams courtesy Robert J. Lang.)
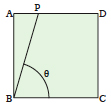 Draw the desired angle PBC so that point B is in the corner of a square of paper.
|
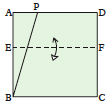 Make a horizontal fold anywhere across the square, defining a line EF.
|
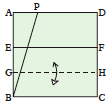 Fold line BC up to line EF and unfold, creating line GH.
|
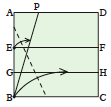 Fold bottom left corner up so that point E touches line BP and point B touches line GH.
|
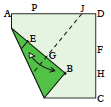 With the corner still up, fold both layers to continue the crease that ends at point G
all the way to J, then unfold. |
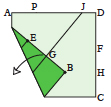 Unfold corner B.
|
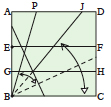 Fold along the crease that runs to
point J, extending it to point B. Fold the bottom edge BC up to line BJ and unfold. |
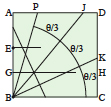 The two creases BJ and BK divide the original angle
PBC into three equal parts. |
Giving this a go yourself will probably convince you that the technique works, but for the skeptical, here is a proof. (NB: This method works for any angle less than 90°. There are other methods that work for larger angles.)
Doubling the cube
Suppose you're given a cube of side length $s_1$ and volume $V$. Your task is to find the side length $s_2$ of the cube which has volume $2V$. Here's how to do this using origami. (Diagrams courtesy Robert J. Lang.)
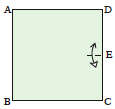 Make a small fold half way up the right side of the paper.
|
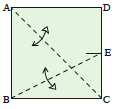 Make a crease connecting points A
and C and another connecting B and E. Only make them sharp where they cross each other. |
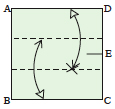 Fold the top edge down horizontally
to touch the crease intersection and unfold. Then fold the bottom edge up to touch with the new crease and unfold. |
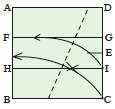 Fold corner C to lie on line AB while point I lies on line FG.
|
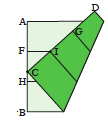 Point C divides edge AB into segments. Work out the ratio AC/CB and multiply this by the side length s1 of the initial cube: the result is the side length s2 you are looking for.
|
In case you're in doubt, here is a proof that this technique works as well.
It's all in the third degree
So what is it about origami that gives it the power to solve these two classic problems? The answer lies in the fact that both problems come down to solving a cubic equation. In the case of the cube, you're looking for the side length $s_2,$ so that $$s_2^3=2V,$$ where $V$ is the volume of the given cube. Since $V=s_1^3$, where $s_1$ is the side length of the given cube, we have $$s_2^3=2s_1^3,$$ which in turn means that $$s_2=\sqrt[3]{2}s_1.$$ Since you know $s_1$, it's really $\sqrt[3]{2}$ you're after. And this is presicely the number we found in the construction above.
An arbitrary angle $\psi$ can be trisected using trigonometry: writing $\psi = 3\theta$ and applying the trigonometric formula for the cosine of a sum of two angles, you get $$\cos(\psi)=\cos(\theta + 2\theta) = \cos(\theta)\cos(2\theta)-\sin(\theta)\sin(2\theta).$$ Now $$\cos(2\theta)=\cos(\theta)^2-\sin(\theta)^2$$ and $$\sin(2\theta)=2\sin(\theta)\cos(\theta). $$ Substituting this into the equation above and simplifying gives $$\cos(3\theta) = 4\cos(\theta)^3-3\cos(\theta).$$ Solving this cubic gives the possible values of $\cos(\theta)$ from which you can work out $\theta$.
It turns out that origami can not only solve the two cubic equations attached to our two problems above, but any cubic equation, that is any equation of the form $$ax^3+bx^2+cx+d=0,$$ for some $a$, $b$, $c$, and $d$. (You can find out how to do this on Kashiro Hatori's website.) And while Euclid's methods can solve quadratic equations geometrically using only straight-edge and compass, they can't solve cubic ones.
Computational origami
One of the pioneers of modern maths-based origami is Robert J. Lang, an American mathematician and origami artist.
In 1989, Lang wrote an article for the magazine Engineering & Science, in which he asked whether a computer could some day design an origami model deemed superior to those designed by humans. It was a question that so intrigued him that in 1990 he set out to write a computer program that could do just that.
From left: Crease pattern formed by TreeMaker, the resulting base, and the finished model. Image courtesy Robert J. Lang.
Within several months, Lang had produced the first version of a piece of software he called TreeMaker (thus called because the figures he used as starting points resembled trees). The program was able to convert a simple line drawing, or stick figure, into a plan for a paper base from which a model could be folded.
In this context a base is a geometric shape that contains flaps corresponding to all of the appendages of the origami model. So a crane, with two wings, a tail and a head is formed from a base with four flaps, while an insect, with six legs, a head and an abdomen, is formed from a base with eight flaps.

Rattlesnake made from one uncut rectangle of Thai unryu paper. Size: 8 inches. Image courtesy Robert J. Lang.
At first, TreeMaker was, in Lang's own words, "little more than a mathematical curiosity". However, over the next eight years, as Lang's understanding of crease patterns grew, he added algorithms to the program. By 1998, TreeMaker was capable of constructing the full crease pattern for a wide variety of origami bases.
Today, Lang has a collection of thousands of origami sculptures. While not all of these have been designed with the aid of TreeMaker, some of his most complicated designs would have been impossible without it. Images of his creations are dispersed trough this article.
Origami technology
While some of the designs by Lang and others are truly astounding, it is easy to dismiss origami as simply art: beautiful but without application in the real world. It comes as somewhat of a surprise, then, to learn that origami techniques are being employed in technologies ranging from space telescopes to car airbags.

Irish elk made from one uncut square of Korean hanji paper. Size: 9 inches. Image courtesy Robert J. Lang.
Ever since the Hubble Space Telescope was launched into orbit by the space shuttle Discovery in 1990, space scientists have been working on its eventual successor. Not one to be accused of a lack of ambition, Roderick Hyde of the Diffractive Optics Group at Lawrence Livermore National Laboratory in Livermore, California, put forward the idea of building a telescope forty times larger than Hubble. The Hubble telescope itself is no small contraption, at 13 metres long and with an aperture of 2.4 metres. The telescope Hyde was proposing would have an aperture of nearly 100 metres, and would be hundreds of metres long. Immediately this posed a logistical problem: even if such a thing could be designed, how would it get into orbit?
The answer came when the researchers realised that it might be possible to construct a foldable lens which could be packed into a space shuttle. The distance between the two ends of the telescope could simply be achieved by placing two lenses in orbit at a suitable distance from each other, where a lack of gravitational force would allow them to stay. Immediately seeing the link with paper folding, the lab contacted Robert J. Lang to ask for his expert opinion.
Over the course of the following year, and with Lang's help, the lab team constructed a prototype called Eyeglass, which is five metres in diameter. Hubble's actual successor, the James Webb Space Telescope to be launched in 2013, does have a mirror that folds up origami-style to be put into a rocket.
For an application closer to home, the development of automobile airbags provides another example of how origami is used. Before an airbag inflates during a crash, it is folded tightly into a compartment within the steering wheel or dashboard. Engineers designing airbags start by modelling the inflation process on computers. In order to do this, they need an algorithm by which to "fold" the fully inflated airbag.
Using an algorithm from his computer program TreeMaker, Lang was able to provide engineers from the German company EASi Engineering with a solution for their folding problem. This was essentially to represent the airbag as a series of polygons, whose edges remained aligned during and after folding — a task that could be achieved with a detailed fold pattern like those Lang was using for his origami models.
A master of origami
For an art that is as old as paper itself, origami has taken an astonishingly long time to reach its potential. Today there are hundreds of other applications being discovered, from helping to build self-assembling robots to providing clues as to how proteins fold into precise three dimensional shapes in the human body. It has taken nearly two thousand years and the birth of the computer to realise just how much is possible, and Lang's creations are testament to just how far we have come.

Praying mantis made from one uncut square of paper. Size: 4 inches. Image courtesy Robert J. Lang.
The incredible applications of origami have well and truly put an end to my early illusions of grandeur, and the belief that I had conquered the world of origami at nine years old with a paper crane. However, for the origami novice, the delight of discovering that you can make such an elegantly simple form from a single sheet of paper and a few folds can make anyone think that they are an origami master. Go on, I urge you to try it — I guarantee you'll be hooked.
About the author

Liz has a biology degree and is currently studying for a Masters in Science Communication at UWE in Bristol. She also worked for a wildlife television company, and in her spare time she enjoys watching Hollyoaks and playing with creepy crawlies.
Comments
Anonymous
Hi!
I loved all of the interesting facts about origami. I'm a middle school math teacher in Charlotte, NC and my students are always interested in learning about this topic. (I'm interested as well). I would like to find out more about how I could collect some of these figures, people who make them, or other origami resources. Do you have any information?
Thanks!
Rachel
The wikipedia page on Mathematics of paper folding has some useful links to other resources at the end. Does anyone else have any suggestions?
Anonymous
An excellent an interesting article - thank you! I have been hooked on Origami ever since I discovered 'Gecko and fly on a wall' by Herman van Goubergen and have often wondered about the mathematics behind it. Given that repeatedly folded paper becomes 'thick' quite quickly, I wonder, does TreeMaker take this into account or does it assume an infinitely thin sheet of paper?
Anonymous
I'm a little confused by the axioms.
Surely the "unique" folds in the first few examples should allow for the mirror-image fold, both mountain and valley bringing the points together?
And Axiom 5 doesn't even work if P1 lies in a circle touching L1 and centred on P2!
Axioms 6 and 7 don't hold if L1 and L2 are parallel.
So, not exactly Axioms, then.
Anonymous
i used this for a research paper so if anything is wrong in this research i'm in big trouble
Anonymous
Don't worry, they work!
You have to understand that these are the "irreducible folds" of origami, so IF THEY ARE POSSIBLE you can just make them without any extra explanation as to how or why they are possible. The last few are to some people unintuitive without a practical demonstration, which is why it is useful to have a list like this.
A person might challenge a folding step which instructs you to fold in a certain way, saying it is inexact or not unique, but then all you need to do is quote the axiom that corrects them.
Anonymous
Heya, great Article thanks,
but the key other than stated is actually Axiom 6,
because Axiom 7 can easily done with line&circle ;)
greets
Simon the Sorcerer
Anonymous
hi... this helped me with my math research paper in honors algebra.
Anonymous
As a wise man once said, every vibration in our earth has mathematics in it. All these great geniuses tried hard to make something out of numbers and that hard work has resulted in providing us a better future. Not directly, but numbers do play a very important role in almost everything.
Denkk
I would like to ask what is the evidence to state that origami originated in China. Paper was inveted in China, but I have my doubts there is factual evidence origami is Chinese. Where are the cranes, dogs, cats, frogs, etc. made by folding paper in China that predates those of Japan? Of so, why isn't origami present in Chinese tradition, why would it disappear all of a sudden leaving no trace of being ever created in China and practised?
Anonymous
Hi, perhaps in the proof of the "doubling the cube" there is a typo. In the penultimate row should be 3x^2 to the second member. Not 3x.
MQ
It was driving so crazy that I had to pull paper and pencil and do some Algebra! Thank you for that! An old professor of mine used to say "I include typos on purpose to see if you are paying attention". Great content!