The power of origami

Share this page
December 2009

Doubling the cube using origami — proof

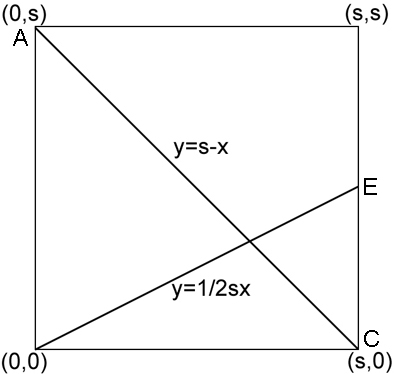
Figure 1
Figure 1

First we show that the first three steps amount to dividing the height of the square into three equal parts. Place the square in a coordinate system with corner $B$ at the point $(0,0)$. See figure 1. Now the line from $A$ to $C$ has equation $y=s-x,$ where $s$ is the side length of the square. The line from $B$ to $E$ has equation $y=1/2x.$ So the two lines meet at a point with $x$-coordinate satisfying $1/2x=s-x,$ so $x=2/3s.$ The $y$-coordinate of the intersection point is therefore $y=s-2/3s=1/3s,$ as required.

The construction claims that the side length $s_2$ of the new cube is $\frac{AC}{CB}$ times the side length $s_1$ of the given cube. Now since $s_2 = \sqrt[3]{2}s_1$, we have $\sqrt[3]{2}s_1 = \frac{AC}{CB}s_1,$ so we need to show that $\frac{AC}{CB}=\sqrt[3]{2}.$

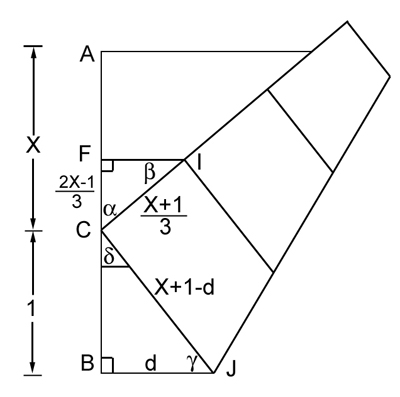
Figure 2
Figure 2

Firstly, we can assume that the length $CB$ is equal to 1, as we can scale the image as we like without affecting the proportions. We'll write $X$ for the length of the line segment $AC$, so the side length of our square is equal to $X+1$. See figure 2. The line segment $BF$ corresponds to two thirds of a side of the square and therefore has length $2\frac{X+1}{3}.$ This implies that the length of the line segment $CF$ is $2\frac{X+1}{3}-1 = \frac{2X-1}{3}.$ We write $d$ for the length $BJ$. Since the line segment $CJ$ is part of the bottom edge, its length is $X+1-d$. There is a right angle at $B$, so by Pythagoras' theorem we have $d^2+1=(X+1-d)^2.$ This means that $d^2 + 1 = X^2+2X+1-2d(X+1)+d^2,$ and therefore $d=\frac{X^2+2X}{2(X+1)}.$ Now consider the two right-angled triangles $CFI$ and $CBJ$. Considering the 180 degree angle formed at $C$ by the vertical edge of the square, we get

  \[ \alpha =180-\delta -90 = 90-\delta . \]    
The angles of the triangle $CBJ$ add up to 180 degrees, so
  \[ \gamma = 180 -90 - \delta = 90-\delta = \alpha . \]    
So the triangles $CFI$ and $CBJ$ have two equal angles: the right angle and the angle $\alpha .$ This means that they are similar. Therefore, the ratios of corresponding sides of the two triagles are equal. Observing that the side $CI$ of the triangle $CFI$ is a third of the side of the square and therefore has length $\frac{X+1}{3}$, we get
  \[ \frac{d}{X+1-d}=\frac{\frac{2X-1}{3}}{\frac{X+1}{3}}=\frac{2X-1}{X+1}. \]    
Substituting the expression for $d$ above gives
  \[ \frac{X^2+2X}{X^2+2X+2}=\frac{2X-1}{X+1}, \]    
so
  \[ X^3+3X^2+2X=2X^3+3X^2+2X-2, \]    
so
  \[ X^3=2. \]    
This proves the result.

Return to main article