As recent articles in PASS Maths have shown, combining the computational powers of modern digital computers with the complex beauty of mathematical fractals has produced some entrancing artwork during the past two decades.

Intriguingly, recent research at the Physics Department of the University of New South Wales, Australia, has suggested that some works by the American artist Jackson Pollock also reflect a fractal structure.

Pollock created many of his works by dripping paint onto enormous canvases, leading to some riotously complex images. While Pollock himself felt that these works reflected "pure harmony", critics have dismissed them as "mere unorganised explosions of random energy". Having examined a number of such paintings produced between 1943 and 1952, the researchers are inclined to agree with Pollock, finding fractal relationships rather than "unorganised explosions" in the paint-drip works.

A feature of fractals is self-similarity on multiple scales: a small chunk of a fractal, scaled up, has similar features to a larger one. The researchers noticed this feature in the paint-splatter works, and analysed a quantity called the fractal dimension of the paintings.

Pollock's drip paintings became more complex over the years. In the early work of 1943, he used single dribbles of paint covering only about 20% of the canvas. By 1952, he was using multiple squiggles covering over 90%. Correspondingly, the researchers found that the fractal dimension of these works increased steadily from a low value close to 1 to a high value of 1.72.

Why is this interesting? Mignon Nixon, a lecturer in American art at London's Courtauld Institute, told the BBC's News Online service: "Mathematical models may be a way of attributing a kind of mastery and order, by shifting from an aesthetic, subjective mode of examination to a more objective, scientific one."

She said that scientific approaches can be useful in the study of art. "If you want to know how was a painting was made or how do we date it, then technical help is crucial. But the information you get that way is also useful for interpretation because you know more about how the thing was made."

Pollock Pic

Jackson Pollock's Number 1, 1950 (Lavender Mist) at the National Gallery of Art in Washington DC.

Extracting beauty from chaos

Andy Burbanks describes the maths behind Lyapunov Exponent fractal images.

Computing the Mandelbrot set

Andrew Williams gets down to detail on computing images of the fractal Mandelbrot Set.

Richard P. Taylor's research

The Research Interests page of Dr. Richard P. Taylor from UNSW, briefly summarising his fractal research (including the Pollock project).

Coda: The Fractal Dimension

An important statistic relating to fractals is the so-called fractal dimension. The fractal dimension is essentially a measure of self-similarity (it is sometimes referred to as the similarity dimension).

First, let's consider the subdivision of some ordinary geometric constructs, all of which have the property of self-similarity (such that they can be constructed out of a series of smaller copies of themselves).

In the one-dimensional case, a line segment can be divided into $N$ identical smaller line segments, each scaled by a ratio of ${1}/{N}$ with respect to the original segment:

In the two-dimensional case, a square can be subdivided into $N$ self-similar smaller squares each of which is scaled by a factor of ${1}/{\sqrt{N}}$ with respect to the original square:

In the three-dimensional case, a cube can be subdivided into N self-similar smaller cubes each of which is scaled by a ratio of ${1}/\left({\sqrt[3]{N}}\right)$ with respect to the original cube:

Extending this, a $D$-dimensional self-similar object can be divided into $N$ smaller copies of itself, each of which is scaled by a factor $r$ where \begin{displaymath} r = \frac{1}{\sqrt[D]{N}} \end{displaymath} or \begin{displaymath} N = \frac{1}{r^D} \end{displaymath} \par From this observation, we define the fractal dimension for a self-similar object of $N$ parts, scaled by a ratio $r$ from the whole, to be: \begin{displaymath} D = \frac{log(N)}{log({1}/{r})} \end{displaymath}

For example, consider the von Koch snowflake curve discussed in Modelling nature with fractals in Issue 6.

To make the snowflake curve, we start off with a straight line segment generator:

This is replaced by the following form, made up of four smaller line segments each one-third the length of the original:

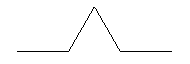
This process is repeated ad infinitum, with each line segment in the snowflake curve being replaced by four smaller segments of one-third its length.

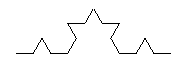
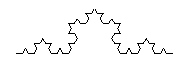
Thus, since any segment of the von Koch snowflake curve is made up of four sub-segments, each scaled by a factor of one third with respect to its "parent", the fractal dimension of the curve can be calculated as follows: \begin{eqnarray*} D & = & \frac{log(N)}{log(1/r)}\\ & = & \frac{log(4)}{log(3)}\\ & \approx & 1.26\\ \end{eqnarray*}

Further Reading: The Science of Fractal Images, Heinz-Otto Peitgen and Dietmar Saupe (Eds.), Springer-Verlag 1988.